介紹

基于梯度下降訓練神經網絡時，我們將冒網絡落入局部極小值的風險，網絡在誤差平面上停止的位置并非整個平面的最低點。這是因為誤差平面不是內凸的，平面可能包含眾多不同于全局最小值的局部極小值。此外，盡管在訓練數據上，網絡可能到達全局最小值，并收斂于所需點，我們無法保證網絡所學的概括性有多好。這意味著它們傾向于過擬合訓練數據。

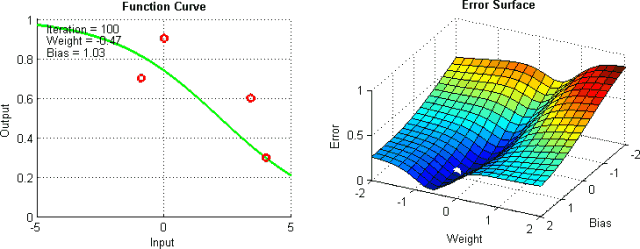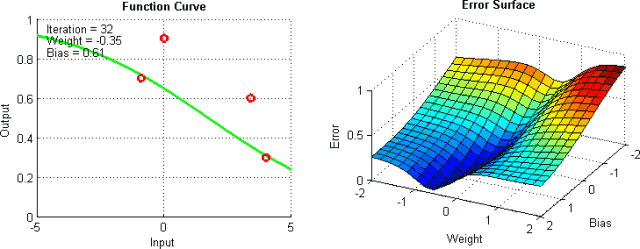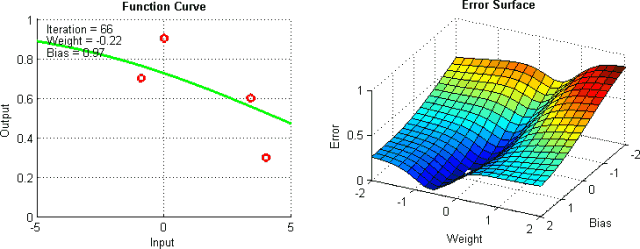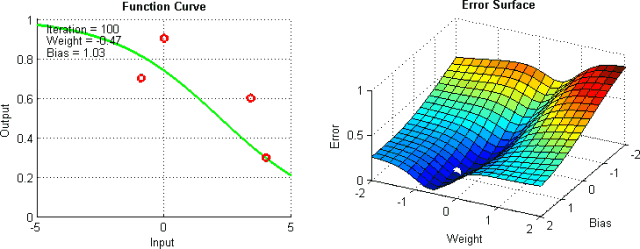
有一些手段有助于緩解這些問題，不過并沒有絕對地預防這些問題產生的方法。這是因為網絡的誤差平面一般很難穿越，而神經網絡整體而言很難解釋。

隨機梯度下降與mini-batch隨機梯度下降

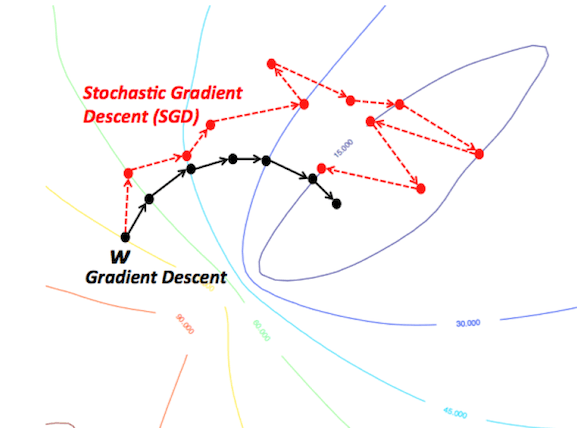
這些算法改編了標準梯度下降算法，在算法的每次迭代中使用訓練數據的一個子集。SGD在每權重更新上使用一個樣本，mini-batch SGD使用預定義數目的樣本（通常遠小于訓練樣本的總數）。這大大加速了訓練，因為我們在每次迭代中沒有使用整個數據集，它需要的計算量少得多。同時，它也有望導向更好的表現，因為網絡在訓練中斷斷續續的移動應該能讓它更好地避開局部極小值，而使用一小部分數據集當有助于預防過擬合。

正則化

正則化基本上是一個懲罰模型復雜度的機制，它是通過在損失函數中加入一個表示模型復雜度的項做到這一點的。在神經網絡的例子中，它懲罰較大的權重，較大的權重可能意味著神經網絡過擬合了訓練數據。

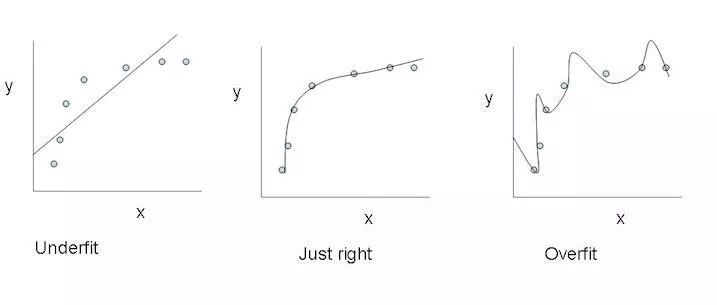
最左：欠擬合；最右：過擬合

若網絡的原損失函數記為L(y, t)，正則化常數記為λ，則應用了L2正則化后，損失函數改寫為如下形式：

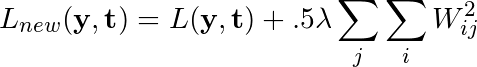
正則化在損失函數中加入了網絡的每個權重的平方和，以懲罰給任何一個連接分配了過多權重的模型，希望能降低過擬合程度。

動量

簡單來說，動量在當前權重更新上加上一小部分前次權重更新。這有助于預防模型陷入局部極小值，因為即使當前梯度為0，之前梯度絕大多數情況下不為0，這樣模型就不那么容易陷入極小值。另外，使用動量也使誤差平面上的移動總體上更為平滑，而且移動得更快。

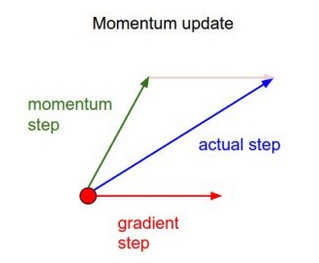
基于這一簡單的動量概念，我們可以重寫權重更新等式至如下形式（α為動量因子）：

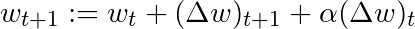
還有其他一些更高級的動量形式，比如Nesterov方法。

學習率退火

我們可以不在整個訓練過程中使用同一學習率，而是隨著時間的進展降低學習率，也就是退火。

最常見的退火規劃基于1/t關系，如下圖所示，其中T和μ0為給定的超參數，μ為當前學習率：

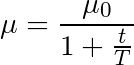
這經常被稱為“搜索并收斂”（search-then-converge）退火規劃，因為直到t達到T之前，網絡都處于“搜索”階段，學習率沒有下降很多，在此之后，學習率減慢，網絡進入“收斂”階段。這和探索（exploitation）與利用（exploration）間的平衡多多少少有些關系。剛開始我們優先探索搜索空間，擴展我們關于空間的整體知識，隨著時間的推進，我們過渡到利用搜索空間中我們已經找到的良好區域，收縮至特定的極小值。

結語

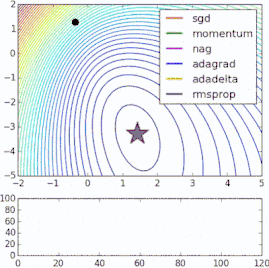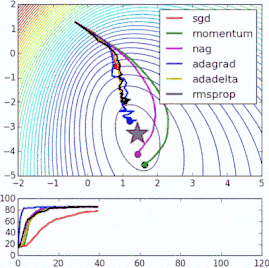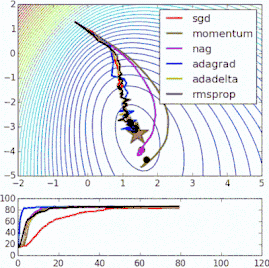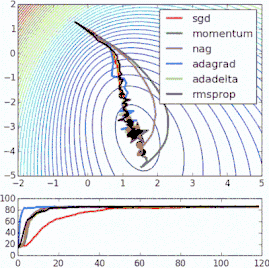
這些改進標準梯度下降算法的方法都需要在模型中加入超參數，因而會增加調整網絡所需的時間。最近提出的一些新算法，比如Adam、Adagrad、Adadelta，傾向于在每個參數的基礎上進行優化，而不是基于全局優化，因此它們可以基于單獨情況精細地調整學習率。在實踐中，它們往往更快、更好。下圖同時演示了之前提到的梯度下降變體的工作過程。注意看，和簡單的動量或SGD相比，更復雜的變體收斂得更快。