隨著航空技術的發展，無人機在軍用與民用領域的應用不斷擴大，如：敵情偵察、地形勘探、地理測繪、目標轟炸、高壓巡線等。無人機執行的任務復雜多樣，為了提高其生存能力，必須實現自主飛行。航跡規劃作為無人機自主飛行的關鍵技術之一，一直是國內外學者們研究的熱點。

航跡規劃可以被看作是優化一系列未知航點集的多約束組合問題，據現有的報道，很多人工智能算法可有效解決該問題。例如，XU C等[3]提出采用人工蜂群算法（Artificial bee colony algorithm，簡稱ABC）去解決無人機航跡規劃問題，并在偵察蜂搜索階段加入混沌算子，取得了不錯的效果；SZCZERBA R J等[4]在A*算法中添加自適應搜索策略，有效去除了規劃空間中的無用航點，提高了算法的搜索時間。然而，上述方法只停留在二維航跡規劃層面上，并未考慮規劃空間中的地形信息和無人機的拐彎角、俯沖角/爬升角以及最短航跡段長度等約束。而三維航跡規劃更符合實際需求，需對其開展研究。近年來，張仁鵬等[5]在建立地形數字模型的基礎上，采用改進粒子群算法來模擬無人機三維航跡規劃，獲得了安全可飛的航跡；ROBERGE V等[6]結合遺傳算法(Genetic Algorithm，GA)與粒子群算法兩者的優勢，采用混合算法解決了無人機三維航跡規劃問題。然而，上述算法隨著搜索空間維數的增加，穩定性和收斂性會隨之下降，也會陷入局部最優值。另外，這些研究也未涉及無人機如何應對突發威脅帶來的影響。

本文采用ABC算法來解決無人機的三維航跡規劃和針對突發威脅時的航跡重規劃問題。同時，為了提供傳統ABC算法的收斂性、魯棒性與穩定性，在雇傭蜂搜索時引入自適應搜索算子、在跟隨蜂搜索時引入新型概率選擇方式及在偵察蜂搜索時引入混沌算子，從而得到了一種改進的ABC算法(Probability self-Adaptive Chaotic Artificial Bee Colony algorithm，PAC-ABC)。然后，對無人機的規劃空間、地形信息和航跡代價模型進行了建模，給出了相應的數學描述。最后，通過三維航跡規劃與突發威脅航跡規劃模擬，驗證了本文所提算法的有效性。

1航跡規劃建模

1.1 規劃空間與地形模型

在三維空間內，無人機航跡規劃問題就是利用規劃算法找出一系列適合飛行且能滿足約束條件的飛行航點集。在無人機實際應用匯總，規劃空間中隱藏著各種威脅信息，如地形、雷達、高炮等，有時這些威脅還具有不確定性，因此想預先獲取飛行空間中的威脅信息具有很大的難度。另外，無人機的續航時間很依賴油耗大小。為了簡化航跡規劃過程，本文提出了以下幾個假設條件：(1)所有規劃空間內的威脅物與地形信息均一致；(2)無人機的油耗與航程成線性關系；(3)無人機的飛行速度保持恒值不變；(4)忽略陣風干擾、機械動力學及機械振動等因素。

用點(xα，yα，zα)來表征規劃空間的某個航點，其中xα為經度值，yα為緯度值，zα為海拔高度，故航跡規劃的規劃空間可描述為[8]：

其中，(x，y)表示山體坐標，(ak，bk)為山體中心對稱軸坐標，hk為山體的最高點。

1.2 航跡代價模型

航跡代價模型由威脅代價模型和油耗代價模型組成。其中，威脅代價主要考慮高炮威脅和雷達威脅[9]。

(1)雷達威脅。通常雷達的探測范圍為圓形，故設雷達對無人機的威脅概率為：

其中，d為雷達中心到無人機的距離，dmax為雷達探測區域的最大半徑。

(2)高炮威脅。和雷達威脅類似，高炮威脅的范圍也為圓形，故設高炮對無人機的威脅概率為：

(3)油耗代價。油耗與航程有關，故認為油耗代價就是總航程。

另外，還應該考慮無人機航跡規劃過程中的其他約束條件：

(1)極限拐彎角。無人機通過控制其偏航角來控制航向的改變。因為存在慣性，飛行過程中要改變航向需要拐彎時間與拐外半徑。記航跡段li在水平面投影為mi=(xi-xi-1，yi-yi-1)，設無人機允許的極限拐彎角為θt，則該約束可被描述成：

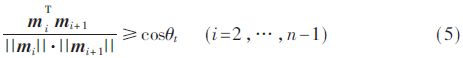
(2)極限俯沖角/爬升角。無人機在高度方向(z方向)上俯沖與爬升的角度限制于其機動性。因此，可設定極限大俯沖角/爬升角為θp的約束方程為：

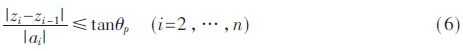
(3)最小航跡段長度。在飛行過程中，當前飛行姿態的改變需要無人機持續飛行一段距離，若無人機偏航角改變頻繁或者大幅度迂回飛行，則會擴大導航誤差，故應盡可能減小航跡長度。設定無人機的最小飛行航跡段長度為lmin，則該約束的數學描述為：

綜上所述，航跡代價模型主要由上述因素構成，故無人機三維航跡代價模型可表示為：

式中，J1～J5分別表征飛行過程中的威脅指標、油耗指標、極限拐彎指標、極限俯沖角/爬升角指標與最小航跡長度指標，wk為相應的權重系數。

2改進的人工蜂群算法

ABC算法是由土耳其KARABOGA D教授提出的一種模擬蜂群協作覓食行為的新興元啟發式優化算法[10]。在算法中，蜜蜂的種類可分為雇傭蜂、跟隨蜂和偵察蜂3種。設蜂群種群總數為N，雇傭蜂和跟隨蜂的數量各占種群總數的一半；每個蜜源均為一個D維向量，其中D表示需要被優化的解個數。在無人機航跡規劃問題，種群中的每只蜜蜂對應一組可行解，ABC算法通過3種蜂種的搜索方式尋找搜索空間的最優解。同時，在算法中添加自適應搜索策略、新型概率選擇策略與Logistic混沌搜索算子。具體的步驟如下所示：

(1)種群初始化。隨機派出N只蜜蜂尋找到xij(i=1，2，…，N；j=1，2，…，D)蜜源，即可行解。蜜源由式(9)產生：

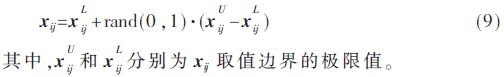
(2)蜜源收益度計算。根據式(10)來計算每只蜜蜂初始時搜索到蜜源的收益度值，并根據蜜源大小排序，取前N/2組解。

其中，Si是ABC算法中的目標函數值。

(3)雇傭蜂搜索階段。在此搜索階段，蜜源信息會因為雇傭蜂的過度挖掘而致使算法迭代速率降低[11]，故本文采用一個自適應搜索策略來改進原搜索方式，即：

(4)跟隨蜂搜索階段。隨著算法迭代次數的增加，種群個體雖會朝著一個方向進化，但同時也會遺漏其他有用信息，從而導致種群多樣性的降低。ABC算法性能的提高在某種程度上依賴于種群多樣性。研究發現，被摒棄的解也含有有用信息[12]。所以，為了使含有較差信息的蜜源同樣能被充分挖掘，本文采用一個新穎的概率選擇方式，來保證種群的多樣性：

(6)記錄當前最優解。當算法遇到終止條件時，輸出迭代過程中的最優解。

3仿真實驗

在本節中，通過一個三維航跡規劃仿真算例對本文所提PAC-ABC算法的有效性進行驗證。另外，也引入傳統ABC算法與GA算法與之進行比較分析。規劃空間采用100 km×100 km×100 km的三維空間。空間中共有5座山峰，疊加的地形信息參數為：

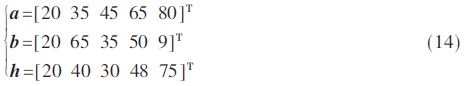
另外，威脅物中的雷達和高炮的分布信息如表1所示。

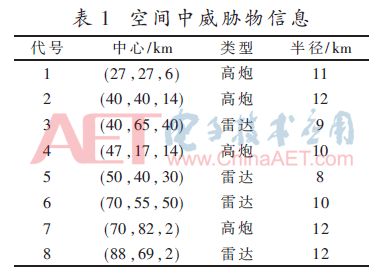
無人機飛行的起始點為(0，0，0)，目標點為(90，80，0)，規劃的維數D=10。采用PAC-ABC算法、ABC算法和GA算法同時去搜索最優航跡。前兩種算法的初始條件設置為：N=20，limit=15。而設置GA算法的條件為：抗體種群數M=20，交叉因子與變異因子分別為0.8與0.2。3種算法各運行10次，每次迭代500次，然后記錄下其中的最優解。航跡規劃的結果如圖1所示。從圖中可以看出，3種算法均能生成可飛航跡，但是ABC算法與GA算法獲得航跡均要翻越山脊，這會導致無人機被發現的概率增加；而PAC-ABC算法獲得航跡則沿著山谷飛行，并較其他兩種算法縮短了航程，利于規避威脅，實現低空突防。

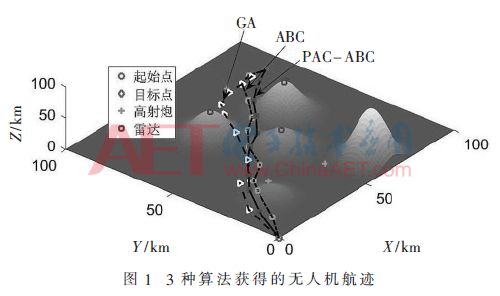
圖2給出了3種算法的迭代曲線，從圖中可以看出本文所提算法的收斂速度最快，在100代左右就能收斂到極值，且航跡代價為51.231 2，而ABC算法和GA算法的航跡代價分別為54.998 0和60.621 4。在改進策略的作用下，PAC-ABC算法能夠較好地避免局部最優值，迅速地尋找到最優解。

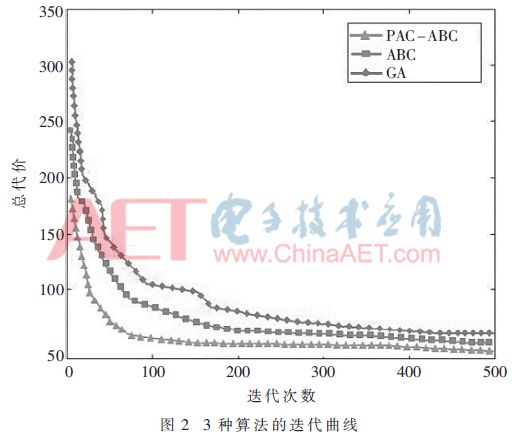
為了進一步驗證PAC-ABC算法的魯棒性，分別取D為20和30時，評價此算法求解無人機航跡規劃問題的效果，仿真結果如圖3所示。從圖中可以看出，隨著維數的增加，PAC-ABC算法依舊能夠尋找到較好的航跡。這說明本文所提算法具有較好的魯棒性。

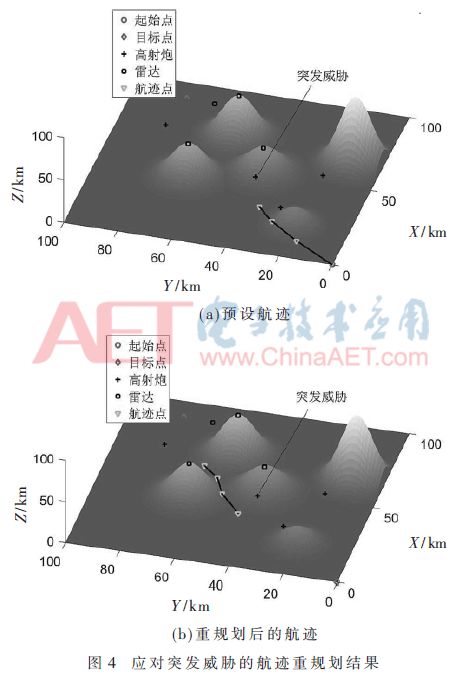
有時，在規劃空間中隱藏著未被發現的突發威脅。當無人機遇到這些突發威脅時，需要算法具有重規劃能力，來規避這些威脅。設無人機從起始點(0，0，0)到目標點(90，80，0)中，在(40，40，13)點處突然偵察到高炮，如圖4(a)所示。若不改變航跡繼續飛行，無人機則有幾率被擊落，故需要對其航跡重新規劃。如圖4(b)所示，通過PAC-ABC算法對航跡再次規劃，可以有效避免突發威脅，規劃時間僅為1.24 s。這說明本文所提航跡規劃算法迭代速率高，具有一定的實時性。

4結論

在處理無人機三維航跡規劃問題時，本文提出了一種改進人工蜂群算法。在算法中，通過自適應搜索策略、新穎的概率選擇方式以及混沌搜索算子，提高了算法的穩定性、搜索快速性與魯棒性。三維航跡規劃實驗表明：(1)與ABC算法與GA算法相比，PAC-ABC算法能夠更快地獲得最優航跡，且航跡代價分別比前兩者少7.35%和18.33%；(2)隨著解維數的增加，PAC-ABC算法依舊能夠獲得較好的解，具有很強的魯棒性；(3)在處理突發威脅時，PAC-ABC算法能夠在較短的時間內實現局部航跡在規劃，保證了無人機的安全飛行。綜上所述，本文所提算法能夠為無人機規劃出一條可飛且較優的飛行路徑。