下面我們來簡單地聊一聊定點小數的常規格式、相對于浮點小數的優勢與劣勢,以及如何使用Lattice ECP3/ECP5的sysDSP乘法器來實現基本的定點小數運算(加法和乘法)。并會在后續的文章中介紹定點小數的除法、平方根、平方根倒數和CORDIC算法的基本理論和HDL的實現等。
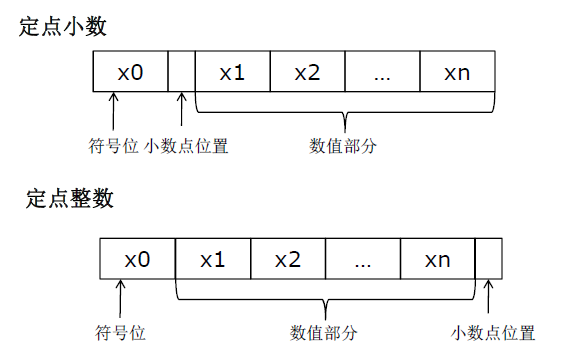
1.定點小數的常規格式
常規的定點小數格式如下圖:
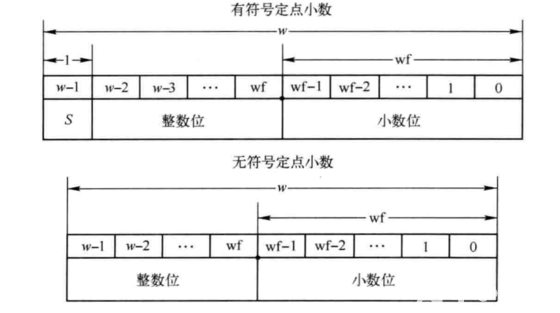
其中,有符號定點小數的值可以表示為:
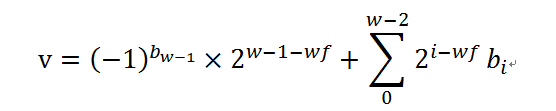
無符號定點小數的值可以表示為:
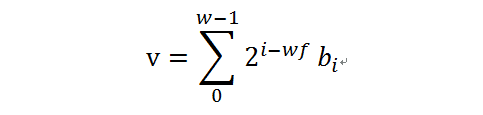
定點數的位寬w和小數部分的位寬wf可以看做是定點數的兩個要素。其中,w決定了定點數的動態范圍,wf決定了定點數的精度。需要注意的是,在進行定點數運算的時候,需要注意數值溢出的問題(包括向上溢出和向下溢出)。所謂向上溢出是指運算結果超出了定點數整數部分所能表示的范圍,向下溢出表示運算結果超出了定點數小數部分所能表示的范圍。顯然,一旦溢出將會造成計算精度的丟失,甚至是計算結果的錯誤。因此,合理地選擇w和wf至關重要,w和wf的值過大會浪費資源,過小又會造成精度丟失。
2.定點數與浮點數的比較
與浮點數相比,定點數具有如下的一些優勢:
(1)更少的資源
通常在FPGA中進行浮點運算時,會消耗更多的LUT、寄存器和乘法器。定點數由于不需要存儲小數點的位置,所以定點數的運算消耗的資源基本上和同樣位寬的整數運算相當,遠遠低于浮點運算的開銷。
(2)更高的性能
浮點運算在消耗更多資源的同時,也會給MAP和PAR帶來壓力,從而導致整個設計的Fmax降低。在同樣規模的運算量下,采用定點數的設計則可以獲得更高的Fmax。
與此同時,相對于浮點數,定點數也有很多的缺陷和不足:
(1)能夠表示數值的動態范圍較小
(2)數值溢出的問題
浮點數由于采用了統一的格式(IEEE-754),且動態范圍很大,因此基本不存在數值溢出的問題。但是定點數則需要程序設計中合理地選取w和wf的值,并且沒有統一的格式規范也為復雜程序的協同設計帶來麻煩。
從應用的需求來看,很多場合下,采用定點數即可滿足系統的性能需求,但是也有一些場合對精度的要求很高,如雷達成像,醫學成像,高精度數據采集與分析等則需要采用浮點數進行運算。
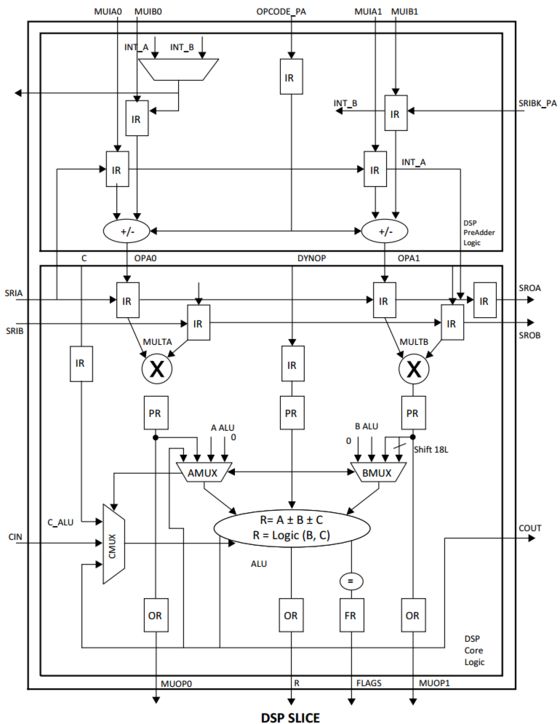
3.ECP3/ECP5 中的sysDSP乘法器
Lattice的ECP3/ECP5系列FPGA內部集成了多個sysDSP架構的乘法器模塊,基于sysDSP,用戶可以便捷地設計出低功耗高性能的數字信號處理應用。相比于用LUT實現的乘法器,基于sysDSP的乘法器具有顯著的性能優勢。此外,Lattice還提供了多種基于sysDSP的IP,如FFT、FIR和CIC等。
ECP5中sysDSP的Slice結構圖如下圖所示:
4.定點小數的加法與乘法
定點小數的加法與乘法運算基本上和普通整數的加法與乘法一致,但是需要注意運算結果的w和wf的與原值的w和wf之間的對應關系。
下面來舉一個簡單的例子:兩個32位的有符號定點小數相乘,其中w=32,wf=23。即

此時,
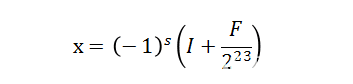
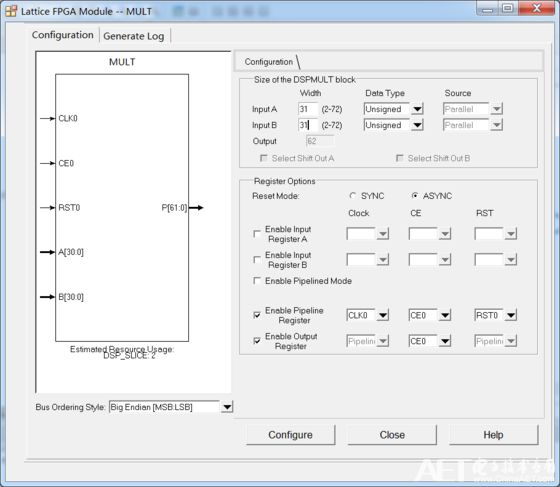
我們可以直接使用Clarity來生成整除乘法器的Module,如下圖所示。其中符號位可以提取出來進行異或操作,剩余的31位進行乘法運算。
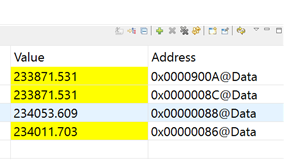
如果需將運算結果也轉換為和輸入相同的格式,則可以進行如下的操作:

上面的例子,是將有符號數轉換為無符號數,再進行運算的(即采用原碼直接運算的)。實際上,我們還可以直接將MULT的Module中的Data Type配置為Signed,此時操作數將以補碼的形式進行運算。
-
FPGA
+關注
關注
1629文章
21743瀏覽量
603558 -
乘法器
+關注
關注
8文章
205瀏覽量
37074
原文標題:【精選博文】FPGA定點小數計算(一)
文章出處:【微信號:ChinaAET,微信公眾號:電子技術應用ChinaAET】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
浮點處理器相對于定點處理器有何不同
第7章 DSP定點數和浮點數
基于牛頓迭代法的FPGA定點小數計算
IEEE 754標準浮點格式可分為哪幾種
定點小數的編碼方法
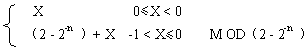
IEEE754浮點數格式
LM4F定點格式于浮點格式的對比和浮點運算的應用詳細中文資料
FPGA定點小數的常規格式、相對于浮點小數的優勢與劣勢和計算的概述





 FPGA定點小數的常規格式、相對于浮點小數的優勢與劣勢
FPGA定點小數的常規格式、相對于浮點小數的優勢與劣勢










評論