低噪放LNA后方的插入損耗對靈敏度有沒有影響?
小編為什么問這樣的問題,難道沒有學噪聲級聯公式?
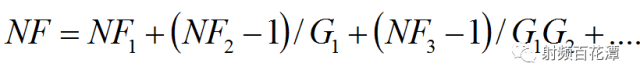
按照以下方式,我在LNA 和IC 之間加個10db 的衰減,對接收靈敏度的影響也很小嗎?
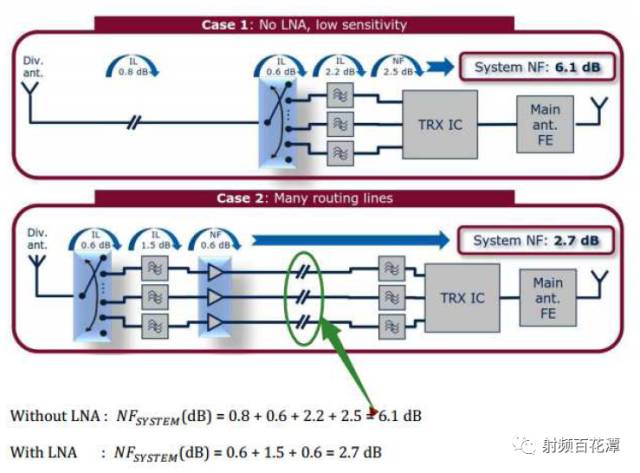
由上面看到了 NFsystem被降低了 6.1-2.7=3.4dB
也就是靈敏度提升了3.4dB
先說結論 要看LNA 后方的Loss 是否遠小于LNA 的Gain
Yes => 沒影響
No => 有影響
先反問個問題 如果說 LNA 之后的Loss 不影響靈敏度
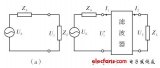
那么 LNA 之后Open(亦即Loss 無限大) 如下圖 :
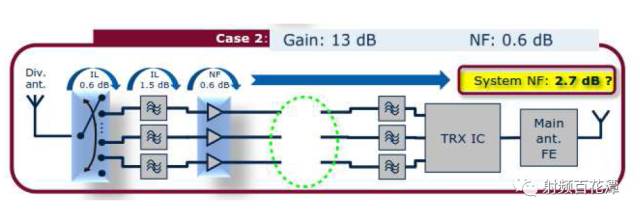
有可能靈敏度不受到影響嗎?? 你第一直覺認為不可能
是吧 因為你連訊號都收不到 何來靈敏度??
要探討LNA 之后的Loss 會不會影響靈敏度
得先知道LNA 之后的Loss 對靈敏度影響程度多大
依據NF級聯公式和Friis Formula :
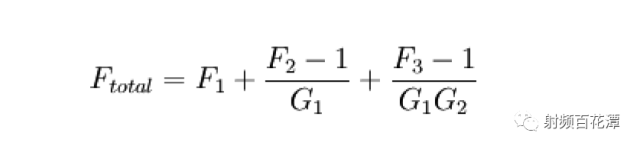
其實計算時 只需以LNA 為分水嶺分前后 換言之
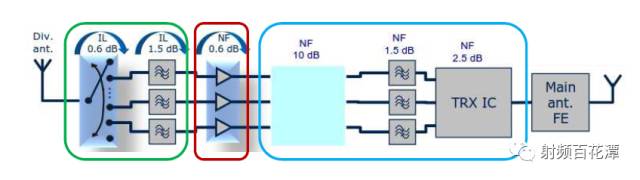
可簡化成三個Block 如上圖的綠框, 紅框, 籃框
計算出來 其NF 為3 dB
而LNA 的Gain 假設為13 dB 也就是G2 要帶19.95
你可以發現 當G2 = 19.95 帶入分母時 其
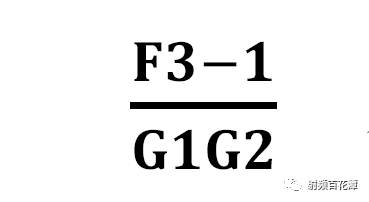
幾乎可忽略不計
換言之
LNA 的Gain 會把LNA 后方Block 對接收路徑整體NF 的貢獻給稀釋掉
因此 若我們只計算綠框跟紅框的NF 總和 可得到2.7 dB
跟上述計算出來的3 dB 差不多
所以才有『LNA 后方的Loss 可忽略不計』的結論
但是 重點來了
F3-1/G1G2之所以可忽略不計
那是因為 (F3-1)遠小于G1G2
以這例子而言
F3-1 = 2
G1G2 = 12.3
F3-1/G1G2= 0.16
反之 如果(F3-1)沒有遠小于G1G2 則
F3-1/G1G2
就不可忽略不計
以反問那題為例 LNA 之后Open
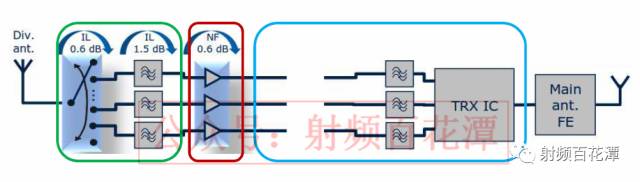
亦即F3 為無限大,代入Friis Formula :
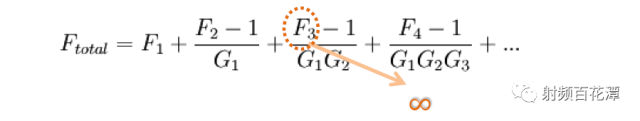
整體接收路徑的NF 變成無限大
再根據靈敏度公式 把整體接收路徑的NF 無限大 代進公式 :
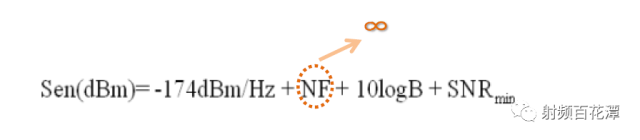
亦即你的靈敏度無限大
這世上不會有無限大的訊號 所以表示你接收機完全收不到訊號
因此 當你(F3-1)沒有遠小于G1G2 時
LNA 后方的Loss 對靈敏度肯定是有影響
由公式也證實了 你的第一直覺是對的
LNA 之后Open 靈敏度不可能不受到影響
因此回到你一開始的問題
『在LNA 和IC 之間加個10db 的衰減,對接收靈敏度的影響也很小嗎?』
我們得計算 加這個10 dB 的衰減后 其(F3-1)有沒有遠小于G1G2
F3-1 = 24
G1G2 = 12.3
很明顯 (F3-1)并沒有遠小于G1G2
所以這10 dB 衰減 對靈敏度肯定有影響
算出來其整體接收路徑的NF 為5.82 dB
而沒加這個10 dB 衰減時 剛計算出來的NF 為3 dB
換言之 你加了這個10 dB 衰減后
其靈敏度劣化了 5.82 – 3 = 2.82 dB 所以有影響
當然 你會說 是否LNA 的Gain 越大越好
這樣越可以使
『LNA 后方的Loss 遠小于LNA 的Gain』這條件成立?
理論上是這樣沒錯
但實際上 LNA 的Gain 若太大
其后方電路會被LNA Output 輸出的訊號灌到飽和
其Noise Floor 上升 SNR 下降 那靈敏度還是不會好
況且LNA 的Gain 越大 其整體接收路徑的IIP3 就會越小
一旦有兩個以上的外來干擾訊號 其產生的IMD3 會越大
因為這IMD3 很靠近RX 訊號 你SAW Filter 也濾不掉
如此一來 IMD3 會讓RX 訊號的Noise Floor 上升 SNR 下降
那靈敏度還是不會好
不好的線性度 連帶也會產生不好的靈敏度
所以LNA 的Gain 不是越大越好 也不是越小越好 而是剛剛好最好
同時也知道 縱然LNA 可使其后方的Loss 不影響靈敏度
但若其后方的Loss 太大 對于靈敏度 還是會有影響
亦即該LNA 改善靈敏度的程度會大打折扣
-
噪聲
+關注
關注
13文章
1122瀏覽量
47439 -
LNA
+關注
關注
4文章
270瀏覽量
57548
原文標題:20180319-低噪放LNA后方的插入損耗對靈敏度有沒有影響?
文章出處:【微信號:EMC_EMI,微信公眾號:電磁兼容EMC】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
濾波器的通帶與插入損耗及頻率
插入損耗對差分對的信號質量影響
從多個方面討論電路的插入損耗,幫助射頻工程師理解電路總的插入損耗的來源
利用外部LNA改善接收機靈敏度
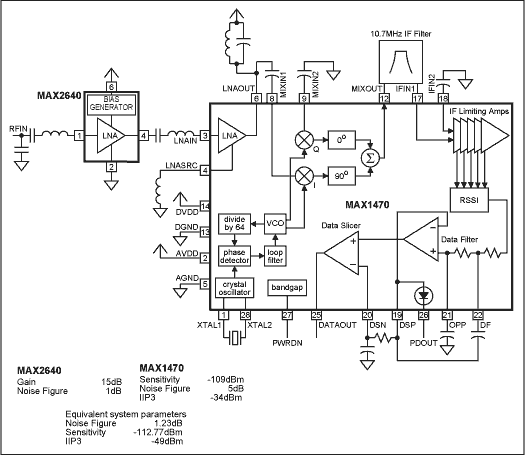
如何用LNA改善GPS的靈敏度
EMI電源濾波器的插入損耗分析




 低噪放LNA后方的插入損耗對靈敏度有沒有影響?
低噪放LNA后方的插入損耗對靈敏度有沒有影響?











評論