數學上的規定：

由于習慣的不同，每個人對同一個事物的標準也不同。

應事先規定好整個項目的一些“習慣”，并堅決貫徹它們，上下統一。

世界坐標系：

場景中所有物體處于世界坐標系下，且所有的坐標系均為左手坐標系，左手坐標系三個軸的指向如圖：

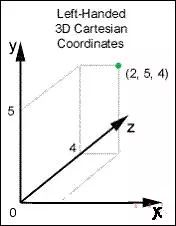
以屏幕為基準，該坐標系X軸指向右，Y軸指向上，Z軸指向屏幕里面。

以此坐標系我們可以創建一個世界空間。當然并沒有真正創建出來，只是一個約定，便于日后的使用。就像地球的經緯度一樣，有了這個我們就能描述什么東西在什么地方了。

物體坐標系：

而世界中有很多物體，比如游戲中的模型，玩家等等。

該世界里的每個物體都含有三個數據：

1）該物體中心處于世界的位置(x,y,z)

2）該物體旋轉的角度(Pitch,Yaw,Roll)。分別對應繞x y z軸旋轉的角度，并規定從各個軸的負方向看過去的順時針方向為正。比如(0,0,90)代表該物體不沿x y軸旋轉，只沿z軸旋轉90度，且旋轉方向為順時針。

3）構成該物體的所有點的相對于物體中心的位置(xi, yi, zi) (i 為構成物體的各個點，比如正方體的 8 個頂點）

光柵化的基礎思想

（假設世界坐標系下只有一個物體，簡化描述）：

1）將該物體的所有點根據該物體在世界的位置及朝向進行縮放、旋轉和平移，這一步將把物體的所有點的坐標從物體坐標系轉換到世界坐標系。

比如某物體只有一個點，該點處于相對物體中心的 (1,0,0) 處，而該物體中心處于世界的 (0,1,0) 處，且沒有經過旋轉。那么該點經過縮放、旋轉和平移的坐標轉換后，可以得到該點在世界坐標系下的位置 (1,1,0) 。

2）將世界中的觀察者（人、玩家、攝像機等等）簡化成一個點，就像一個攝像機，該攝像機便是觀察的視線發出的地方。同時攝像機也有如物體一樣的位置信息 (x,y,z) 及旋轉角度信息 (pitch, yaw, roll)。通過這兩組數據我們可以求出攝像機在世界坐標系下的位置以及視線的朝向。

但將要進行的動作恰恰相反，我們將世界的所有點（經過第一步后這些點的坐標系已經從他們的物體坐標系轉換到了世界坐標系）進行上述變換的逆變換，可以得到以攝像機為中心的所有點的坐標。這一步之后的世界空間改叫觀察空間。

3）將觀察空間轉至齊次剪裁空間。在實際生活中攝像機（或者人類）看東西的范圍是有限的。但是目前為止所有的點不論攝像機看不看得到，都經過了變換。所以還要將觀察空間中的所有點轉換到一個叫做齊次剪裁空間的空間。這個空間有一個長寬高均為2的人為劃定的范圍，且該立方體形的范圍的中心處于原點(0,0,0)。

也就是說，這個范圍上下前后左右的范圍是 -1 到 1 。經過一個特殊的矩陣乘法變換后，所有處于該 2x2x2 立方體形范圍內的所有點，都將是看得到的，最終會被渲染出來的。所有不在該 2x2x2 大小的范圍內的點，都處于視線之外，最后都將不會渲染出來。盜張圖：

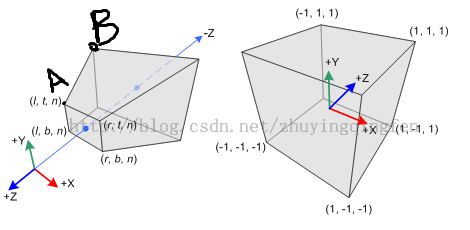
左邊是觀察空間，原點處是我們的攝像機（這個坐標系不是我們使用的左手坐標系，這是右手坐標系，他的 z 軸朝向屏幕外）。右邊是第三步轉換后形成的齊次剪裁空間。

目前已經把所有點都轉換到了這個齊次剪裁空間，并且剪裁掉了一切不在該立方體包圍內的點。

這時候我們已經可以把各個點的x、y坐標拿來，經過插值匹配到顯示器的分辨率后（即將每個點的x y坐標的數值從[-1,1]“拉伸”至譬如[0,1920]和[0,1080]），直接顯示出來了。但是顯示的結果會比較奇怪，遠近不同的物體大小居然一樣。該投影過程叫做正交投影，而日常生活中我們所看到的近大遠小的世界是透視投影的結果。

怎么進行透視投影？大致思路是將每個點的在觀察空間下的z坐標拿來，除以該點在齊次剪裁空間下的x和y的值（x = x/z, y = y/z）。顯示出來便是透視投影后的圖像。

簡短總結：

要想將構成三維世界的點轉換到顯示器這個二維平面上來，需要對每個點進行如下操作

1）物體空間轉換至世界空間 （通過數個矩陣乘法）

2）世界空間轉換至觀察空間 （需求出攝像機變換的逆矩陣）

3）觀察空間轉換至齊次剪裁空間 （通過乘上特殊的變換矩陣）

4）進行透視除法 （除以特定 z 值）

但是以上變換只是得到了點最終的位置信息。要想顯示在屏幕上，還需要填充點和線組成的面，甚至是賦上自定義的貼圖。