長短期記憶網絡（Long Short-Term Memory，LSTM）是遞歸神經網絡（Recurrent Neural Network，RNN）的一個變種，專門設計用來解決標準 RNN 在處理長序列數據時遇到的梯度消失或梯度爆炸問題。標準 RNN 在反向傳播過程中，由于鏈式法則的應用，梯度可能會在多層傳播中指數級地減小（梯度消失）或增大（梯度爆炸），這使得網絡難以學習和記住長時間步的依賴關系。

1.遞歸神經網絡（RNN）

RNN 的核心是其循環結構。在每個時間步，RNN 不僅接收當前輸入數據，還接收前一時間步的隱藏狀態，正是隱藏狀態的設計，使得網絡能夠記住和利用之前的信息。

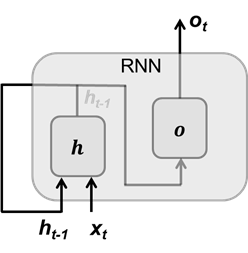
圖 1 RNN 單元結構

圖1顯示了標準 RNN 的單元結構，其中輸入向量xt，輸出向量ot，隱藏狀態向量ht-1。當前隱藏狀態向量ht的計算如下，其輸入當前時間步向量xt和前一時間段步的隱藏狀態向量ht-1：

其中 σ 表示激活函數，Wh 和 Wx 是隱藏狀態變換參數和輸入變換參數，隱藏狀態負責記憶之前時間步上的信息。RNN 的輸出向量ot是對隱藏狀態做線性變換：

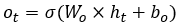其中 σ 表示激活函數，Wo?輸出變換。Wh 、Wx 和 Wo 是 RNN 要學習的參數。標準的 RNN 結構存在兩個主要問題：梯度消失（或增大）；長期信息丟失。

梯度消失（或增大）在長時間序列中，梯度是消失還是增大，與選擇的激活函數有關，這里我們解釋梯度消失問題。假設損失函數為 L，在反向傳播過程中，針對參數 Wh的梯度計算為：

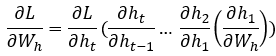
而?h1/?wh是通過激活函數做梯度計算，激活函數的取值范圍是[-1,1]（tanh函數）或[0,1]（sigmod函數），因此，連續相乘會產生梯度消失，

長期信息丟失對當前隱藏狀態向量產生影響的是當前時間步的輸入向量和前一個時間步的隱藏狀態向量。當前輸入數據往往是會攜帶大量信息，而隱藏狀態變量是遞歸生成的，隨著遞歸次數的增加其變化量也會較少，因此 Wx × xt 的值會大于 Wh × ht-1。

▼

2.長短期記憶（LSTM）

LSTM 是一種新的 RNN 結構，能夠有效地保留長期信息并緩解梯度消失問題。LSTM 引入了一個記憶單元（也是單元狀態向量），用于存儲長期信息。記憶單元通過直接的線性連接在時間步之間傳遞信息，避免了梯度消失問題。LSTM 通過三個門（遺忘門、輸入門和輸出門）來控制信息在時間步間的流動量。

遺忘門: 決定記憶單元中哪些信息需要丟棄。

輸入門: 決定哪些新的信息會被加入記憶單元。

輸出門: 控制記憶單元的輸出部分如何影響最終的輸出。

LSTM 的單元結構如圖2所示。其中，f、i、o分別是遺忘門、輸入門和輸出門，g表示候選進入單元狀態的信息；σg 和σc表示激活函數，?表示向量對應元素相乘。

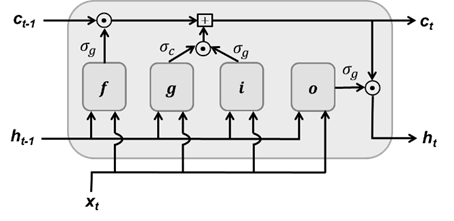
圖 2 LSTM 單元結構 每個門對輸入數據和前一時刻的隱藏狀態向量的轉換過程可以表示為：

遺忘門：

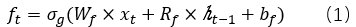
輸入門：

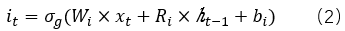
輸出門：

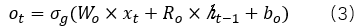
候選狀態單元：

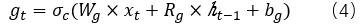
進一步，單元狀態（cellstate）表示為：

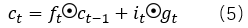
隱藏狀態（hidden state）表示為：

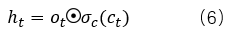
一般情況下，激活函數σg 和σc分別采用tanh函數和sigmod函數。正如公式（5）所示，t時刻的單元狀態ct，是對前一時刻的單元狀態做部分遺忘，遺忘的比例由遺忘門ft 決定；并增加部分輸入數據，增加的比例由輸入門決定it。而公式（6）表明，每個時間步的隱藏狀態是部分單元狀態，比例部分由輸出門ot 決定。

正是由于單元狀態的引入，可以通過一條直接的路徑記住每個時間步的輸入數據，也就是長期依賴關系；而輸入數據通過加法（類似于殘差）引入單元狀態中，使得反向傳播過程的梯度消失得到緩解。 ▼

3.MATLAB 對 LSTM的支持

在 MATLAB 中，lstmLayer 層實現了 LSTM，其提供了多個屬性用于設置和初始化 LSTM 的相關參數。

MATLAB 中的 lstmLayer 及其屬性

例如NumHiddenUnits用于設置隱藏狀態向量的維度，隱藏狀態包含來自所有先前時間步的信息，其大小也決定了 LSTM 要學習的參數的規模；stateActivateFunction設置單元狀態和隱藏狀態的激活函數；gateActivateFunction用于設置門操作的激活函數；還有一個很重要的屬性outputMode，其有兩個值：sequence和last。LSTM 單元按時間步順序處理輸入數據，輸出是當前時間步的隱藏狀態，如圖 3 所示。如果outputMode的屬性值為 sequence，每個時間步的隱藏狀態向量都會輸出，最終 lstmLayer 輸出一個隱藏狀態序列，序列長度等于輸入序列的長度；如果outputMode的屬性值為 last，那么 lstmLayer 只輸出最后一個時間步的隱藏狀態向量。由于 LSTM 是對輸入序列遞歸處理，所以最后一個時間的輸出隱藏狀態向量已經包含其與之前所有時間步的依賴關系。

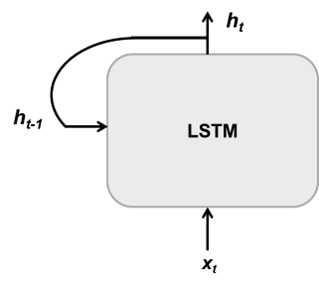
圖3（a）LSTM單元的每個時間步的輸入數據和輸出數據；

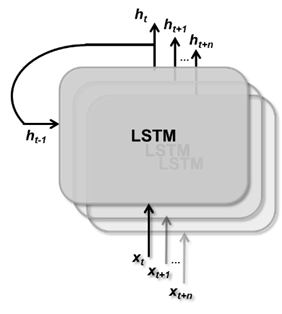
圖3(b) LSTM遞歸處理輸入序列，并生成相應的輸出序列

MATLAB 還同時支持 BiLSTM（BiderectionalLong Short-Term Memory），也就是雙向 LSTM。BiLSTM 是對 LSTM 的擴展，通過引入雙向信息流來增強模型的上下文捕獲能力。在 BiLSTM 中，輸入序列不僅從前向后處理（正向 LSTM），還從后向前處理（反向 LSTM）。這種雙向處理方式允許模型在每個時間步上同時考慮前后文信息，從而提高預測的準確性。

類似于 lstmLayer，MATLAB 中的 bilstmLayer 實現了 BiLSTM。屬性NumHiddenUnits用于設置隱藏狀態向量的維度，其包含先前時間步和后續時間步的信息，而實際輸出的隱藏狀態向量維度為 2*NumHiddenUnits，即將前向和后向兩個處理過程的隱藏狀態進行連接。 ▼

4.LSTM 在基于信號數據的故障診斷中的應用

基于 LSTM，可以構建分類網絡對設備或器件做故障診斷。LSTM 可以捕獲傳感器數據在時間上的依賴關系，進而可以識別設備的動態特性實現診斷或預測。使用 Deep Network Designer App 構建分類網絡，如圖 4 所示。

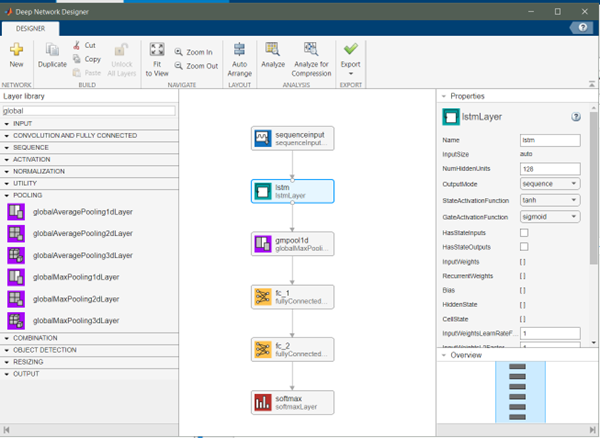
圖4 LSTM分類網絡

lstmLayer 的隱藏單元向量維度設置為 128，outputMode設置為sequence，因此，lstmLayer 層的輸出是一個隱藏狀態向量序列，并且序列中的每個向量的維度為 128。在 lstmLayer 之后使用 globalMaxPooling1dLayer 層對輸出結果在時間方向上做最大值池化（這類似在傳感器數據的深度學習模型應用（一） – Transformer中使用的方法），進而其輸出結果為一個128維的向量，最后我們使用兩個全連接層做線性變化，最終輸出為 3 維的向量對應于故障種類。

使用在傳感器數據的深度學習模型應用（一） – Transformer提到的數據集，該數據集是對原始信號數據做了時域、頻域、以及時頻域的特征提取，進而將具有 146484 采樣點一維數據，轉換為 1464×30 的二維矩陣（因此，在 LSTM 分類網絡中輸入層的維度為 30）。數據集進步劃分為訓練集和測試集，如下所示：

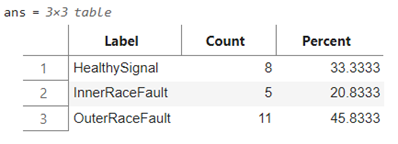
訓練集(上)

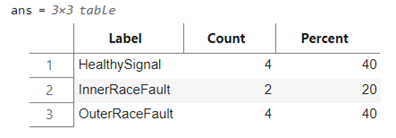
測試集(下)

模型訓練過程，MATLAB 提供了超參數選項實現模型的進一步調優，而超參數選項是通過 trainingOptions 函數設置的，包括初始學習速率、學習速率衰減策略、minibatch 大小、訓練執行環境（GPU、CPU）、訓練周期等等。經過 100 個 Epoch 訓練，模型在測試集上的測試結果如圖 5 所示：

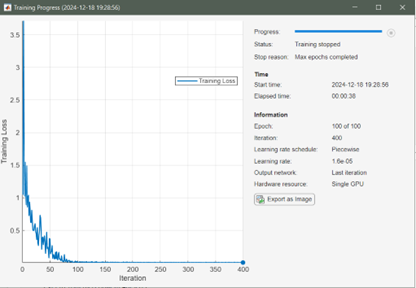
圖 5 模型訓練過程（上）

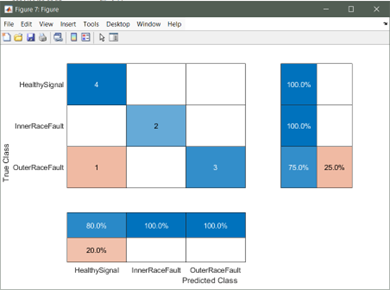
圖 5測試集精度（heatmap）(下)

▼

5. 總結

本文的目的主要是介紹 Long-shortterm memory(LSTM)，以及 MATLAB 對 LSTM 支持和如何在 MATLAB 中構建基于 LSTM 的分類網絡。當然基于 LSTM 還可以構建回歸網絡，實現序列到一個值和序列到序列的預測。本文目的是給讀者在序列數據分析提供一種思路，文中的模型設計和訓練還有可以優化地方，僅為讀者提供參考，也歡迎大家做進一步模型結構調整和精度提升。