邏輯異或運算簡介

邏輯異或運算簡稱異或。異或，英文為exclusiveOR，縮寫成xo。異或（xor）是一個數學運算符。它應用于邏輯運算。異或的數學符號為“⊕”，計算機符號為“xor”。其運算法則為：

a⊕b=（?a∧b）∨（a∧?b）

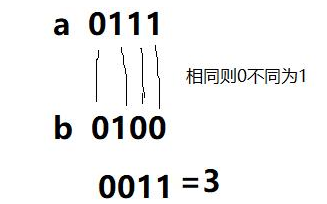
如果a、b兩個值不相同，則異或結果為1。如果a、b兩個值相同，異或結果為0。

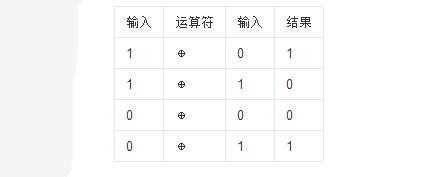
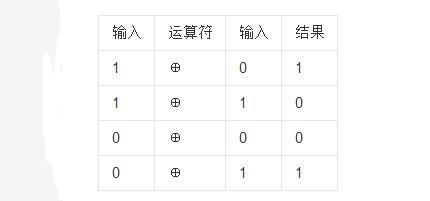
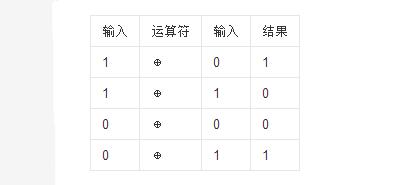
異或也叫半加運算，其運算法則相當于不帶進位的二進制加法：二進制下用1表示真，0表示假，則異或的運算法則為：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同為0，異為1），這些法則與加法是相同的，只是不帶進位。

邏輯異或運算性質

1、交換律

2、結合律（即（a^b）^c==a^（b^c））

3、對于任何數x，都有x^x=0，x^0=x

4、自反性AXORBXORB=Axor0=A

異或運算最常見于多項式除法，不過它最重要的性質還是自反性：AXORBXORB=A，即對給定的數A，用同樣的運算因子（B）作兩次異或運算后仍得到A本身。這是一個神奇的性質，利用這個性質，可以獲得許多有趣的應用。例如，所有的程序教科書都會向初學者指出，要交換兩個變量的值，必須要引入一個中間變量。但如果使用異或，就可以節約一個變量的存儲空間：設有A，B兩個變量，存儲的值分別為a，b，則以下三行表達式將互換他們的值表達式（值）：

A=AXORB（aXORb）

B=BXORA（bXORaXORb=a）

A=AXORB（aXORbXORa=b）

類似地，該運算還可以應用在加密，數據傳輸，校驗等等許多領域。

邏輯異或運算怎么算

邏輯異或運算簡稱異或。英文為exclusiveOR，或縮寫成xor。

異或（xor）是一個數學運算符。它應用于邏輯運算。異或的數學符號為“⊕”，計算機符號為“xor”。其運算法則為：

a⊕b=（?a∧b）∨（a∧?b）

如果a、b兩個值不相同，則異或結果為1。如果a、b兩個值相同，異或結果為0。

異或邏輯

邏輯表達式：F=AB’⊕A’B（（AB’⊕A’B）’=AB⊙A’B’，⊙為“同或”運算）

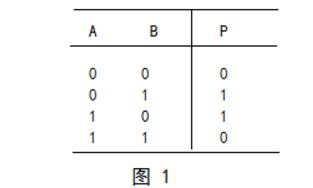
異或邏輯的真值表如圖1所示

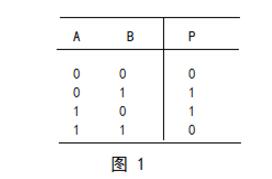
示，其邏輯符號如圖2所示。異或邏輯的關系是：當AB不同時，輸出P=1；當AB相同時，輸出P=0。“⊕”是異或運算符號，異或邏輯也是與或非邏輯的組合，其邏輯表達式為：

P=A⊕B

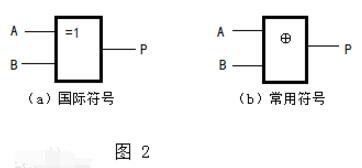
由圖1可知，異或運算的規則是

0⊕0=0，0⊕1=1

1⊕0=1，1⊕1=0

口訣：相同取0，相異取1

事實上，XOR在英文里面的定義為eitherone（isone），butnotboth，也即只有一個為真（1）時，取真（1）。

邏輯異或運算應用

1-1000放在含有1001個元素的數組中，只有唯一的一個元素值重復，其它均只出現一次。每個數組元素只能訪問一次，設計一個算法，將它找出來；不用輔助存儲空間，能否設計一個算法實現？

解法一、顯然已經有人提出了一個比較精彩的解法，將所有數加起來，減去1+2+.。.+1000的和。

這個算法已經足夠完美了，相信出題者的標準答案也就是這個算法，唯一的問題是，如果數列過大，則可能會導致溢出。

解法二、異或就沒有這個問題，并且性能更好。

將所有的數全部異或，得到的結果與1^2^3^.。.^1000的結果進行異或，得到的結果就是重復數。

但是這個算法雖然很簡單，但證明起來并不是一件容易的事情。這與異或運算的幾個特性有關系。

首先是異或運算滿足交換律、結合律。

所以，1^2^.。.^n^.。.^n^.。.^1000，無論這兩個n出現在什么位置，都可以轉換成為1^2^.。.^1000^（n^n）的形式。

其次，對于任何數x，都有x^x=0，x^0=x。

所以1^2^.。.^n^.。.^n^.。.^1000 = 1^2^.。.^1000^（n^n）= 1^2^.。.^1000^0 = 1^2^.。.^1000（即序列中除了n的所有數的異或）。

令，1^2^.。.^1000（序列中不包含n）的結果為T

則1^2^.。.^1000（序列中包含n）的結果就是T^n。

T^（T^n）=n。

所以，將所有的數全部異或，得到的結果與1^2^3^.。.^1000的結果進行異或，得到的結果就是重復數。

當然有人會說，1+2+.。.+1000的結果有高斯定律可以快速計算，但實際上1^2^.。.^1000的結果也是有規律的，算法比高斯定律還該簡單的多。

google面試題的變形：一個數組存放若干整數，一個數出現奇數次，其余數均出現偶數次，找出這個出現奇數次的數？

解法有很多，但是最好的和上面一樣，就是把所有數異或，最后結構就是要找的，原理同上