隨著系統功能的日益復雜,以自適應控制為代表的先進控制理論與算法越來越多地被投入到工程應用當中。而隨著大家對被控物理系統特性本身和控制理論更加深入的研究,像魯棒控制、模型預測控制、模糊邏輯控制,甚至是強化學習,都逐漸成為了控制工程師口袋中的武器。
然而對于傳統的嵌入式應用而言,成本上的考量使得硬件算力的進一步提升成為一種奢望,也從一定程度上限制了更加“智能”的控制算法的應用。例如在自動駕駛或者自主系統控制領域頗為流行的非線性模型預測控制,很難直接應用于算力更加緊張,但也更廣泛的傳統嵌入式場景當中,工程師們也只能去選擇更加“簡化”的控制算法來實現部署,這也是為什么在傳統的嵌入式控制場景中,基于經典線性控制理論的PID 控制器依然很流行。
但隨著被控對象系統的動態越來越復雜,其非線性程度、外部擾動和不確定性越來越高,PID 明顯力不從心。相比于直接使用類似非線性模型預測控制這類運算復雜、對硬件算力要求極高的控制算法,工程師們開始越來越多地探索如何在傳統 PID 控制中添加一些“自適應”因素,讓其能夠在有限的硬件資源限制下,盡可能地響應和處理真實物理系統中的未知干擾與不確定性,從而也能達到更好的控制效果。
MathWorks 作為工具廠商也在積極響應用戶類似的需求,在過去的幾個版本中,陸續添加了諸如模型參考自適應控制、自抗擾控制和模型預測控制等功能(詳見之前的文章《讓閉環控制器的參數調節事半功倍-SimulinkControl Design更新探討》)。在今天的文章中,我們將重點討論在24b 版本中新添加的滑模控制(Sliding Mode Control, SMC)模塊支持以及相關案例。
滑模控制(SMC)是一種以其魯棒性和高效性著稱的非線性控制策略。自 20 世紀 50 年代首次提出以來,滑模控制因其在處理不確定性系統和外部擾動方面的卓越性能,逐漸成為自動控制領域的重要研究方向。滑模控制的最大優勢在于其對系統參數變化和外部干擾的強魯棒性,這使得它在實際應用中能夠有效應對各種不確定性(包括不限于系統的非線性特性、外部擾動等等)。此外,滑模控制結構簡單,易于實現,且能夠提供快速的動態響應,在傳統嵌入式應用硬件算力受限的情況下依然適用。在現代控制系統中,滑模控制被廣泛應用于電機控制、機器人系統、車輛動態控制以及航空航天等領域。
滑模控制原理概述
聽起來滑模控制無所不能是不是?它是如何保證上述這些優勢的?這就需要簡單介紹一下它的原理。
滑模控制是一種特殊的變結構控制,它與常規控制的區別在于控制的不連續性,其核心思想是根據系統所期望的動態特性來設計一個滑模面(Sliding Surface),通過控制器使系統狀態從滑模面之外向其快速收斂并保持在該面上。系統一旦到達滑模面,控制器通過反饋控制將保證系統沿該面到達系統原點(目標穩態工況)。由于系統的特性和參數只取決于設計的滑模面而與外界干擾沒有關系,所以滑模控制具有很強的魯棒性。
文字看起來比較繞?我們用下面的公式來幫助理解。
考慮用如下公式表征的一般非線性系統,
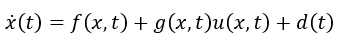
其中,代表系統固有的動態特性,代表控制輸入對系統的影響,則反應了隨時間影響系統行為的外部干擾。
該公式反映了系統本身的動態特性,控制輸入和外部未知干擾的耦合。如前面我們提到的,SMC 是一種變結構的控制,其在兩種不同的結構之間切換,從數學上描述為:
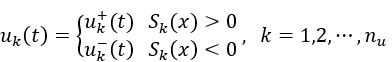
在這里,我們分別定義了兩組不同的控制輸入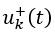 和
和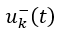 ,分別用于系統處于滑模面的不同側。假設系統有 nu?個控制輸入,則 nu?個 Sk?便可以組成滑模面函數?S(x)。
,分別用于系統處于滑模面的不同側。假設系統有 nu?個控制輸入,則 nu?個 Sk?便可以組成滑模面函數?S(x)。
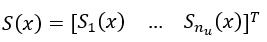
為了保證狀態變量能夠收斂于滑模面,并保持其軌跡始終沿著滑模面,合理設計控制輸入u和滑模面S(x)至關重要。當系統狀態到達滑模面后,滑模面函數能夠滿足S(x)=0,要使得如前述公式所示的一般非線性系統能夠達到并穩定在滑模面中,我們必須要求滑模面與其導數滿足如下關系:
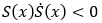
我們可以用如下的平面圖來解釋這樣的關系,假設圖中的直線表示滑模面S(x),其導數必須與S(x)呈相反的符號,才能保證系統狀態穩定在S(x)上。
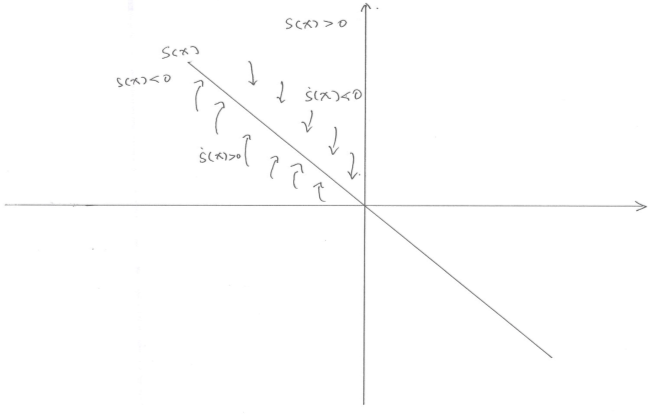
圖1 滑模面的二維等效解釋
那么如何來快速定義控制輸入和滑模面呢?顯然如果沒有工具加持,大多數情況下我們依然無從下手。在最新的 MATLAB R2024b 版本中,用戶可以使用 SlidingMode Controller (Reaching Law)[1]模塊,使用一種動態調整控制動作(趨近率,ReachingLaw)以有效地將系統狀態引導到滑模面,從而實現滑模控制。在該模塊中,我們支持兩類滑動模態模式,以幫助用戶快速定義滑模面函數和控制輸入。
第一類:調節模式,當我們希望將系統穩定在一個固定工況點時使用此模式,此時系統的所有狀態變量 x為零,
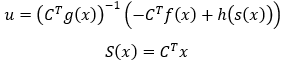
第二類,跟蹤模式,通常情況下,閉環控制希望的是讓系統的狀態跟隨一個參考的軌跡指令 xref。
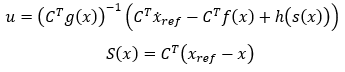
易見,第一類問題是第二類問題的一種特殊情況。在上述公式中,滑動系數矩陣 C決定了滑模面S(x)的形狀,我們可以用它來定義滑模面 S(x)。h(s(x)) 則被叫做趨近率(Reaching Law),它表征了系統以什么樣的動態特性收斂并保持在滑模面上,我們用它來定義控制輸入 u,Reaching Law 有幾種不同的方式,在現有模塊中提供了三種方式:
恒定速率(Constant rate):系統以恒定速率達到滑模面,較大的恒定速率可以使得系統更快地收束到滑模面,但可能會引發執行器控制飽和或者控制不穩定。
指數速率(Exponential):通過給恒定速率添加比例增益項以避免恒定速率引發的問題,比例增益項使得系統狀態偏離滑模面較大時提供更快的收斂速率,而在偏差變小時作用減弱。
功率比(Power Rate):不同于固定常數的比例增益,通過增加一個0到1之間的系數 來平滑調節系統狀態與滑模面偏差不同時的收斂速度,以兼顧收斂速度和平穩性。
典型案例分析之一彈簧阻尼系統
公式介紹完了,相信大家能夠了解滑模控制的基本原理,知道在滑模控制中,最重要的是定義滑模面S(x)和控制輸入 u,也知道 MATLAB/Simulink 現在有“即插即用”的模塊來幫助我們定義。但如果要向其它人解釋什么滑模面S(x),以及如何通過調節它來提升滑模控制的性能,作者在寫到這里的時候也跟大家一樣都是一頭霧水。因為相比于那些傳統的控制理論,這個不是平面,卻又叫做“面” S(x)的實在是太過抽象,干憑冥想理解它著實不容易。我們需要一個簡單的物理場景來具像化它,幫助我們理解。在 MATLAB R2024b的幫助文檔中就給出這樣一個例子,SlidingMode Control Design for Mass-Spring-Damper System[2],下面就讓我們一起來探討一下。
我們考慮如下一個簡單的質量-彈簧-阻尼系統,視為質點的質量為 M 的質量塊,在彈性系數為 K,阻尼系數為 D 的約束下,被大小為 F 的力驅動(視為控制輸入)。
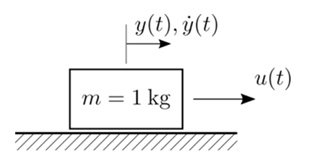
圖2 質量-彈簧-阻尼系統示例
我們可以很輕易地得到反映其動態的系統方程,
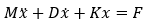
其中,x 代表質量塊的橫向位移,即圖中的y,那么 x ?和 x自然代表它的速度和加速度。
等一下,這個系統動態的方程跟我們一開始定義的一般非線性系統表征不太一樣,為了保持一致,我們需要先做一些修改,
我們在系統中定義兩個變量,橫向位移為 x?,速度為 x?,則系統動態可以表示為
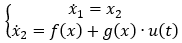
其中,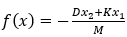 ,
,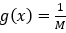 。 為何選了這樣一個系統?因為如果我們將系統中的兩個狀態分別置于平面坐標系的橫軸和豎軸上,它就會形成一個“平面”。
。 為何選了這樣一個系統?因為如果我們將系統中的兩個狀態分別置于平面坐標系的橫軸和豎軸上,它就會形成一個“平面”。
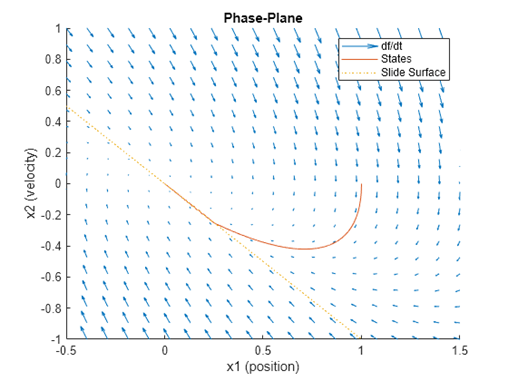
圖3 質量-彈簧-阻尼系統相平面
由圖上我們可以知道,系統的“軌跡”(兩個狀態變量的變化),永遠是跟隨著圖中藍色的箭頭來行進,即位移絕對值達到最大值時,速度都是零。那么在圖中,我們可以找到這樣一條分割線,x?+x?= 0,無論當系統的工作狀態處于分割線左邊或者右邊時,都會向這條線“收斂。”
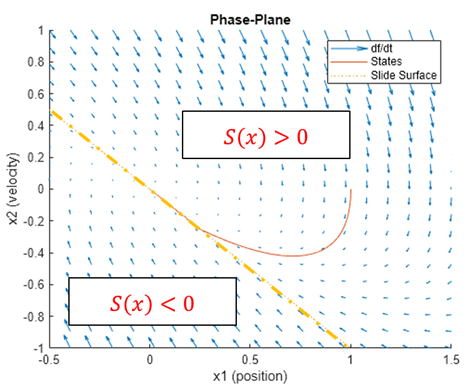
圖4 質量-彈簧-阻尼系統滑模面
顯然,圖中這條線就滿足之前我們對滑模面S(x)的討論,在這個例子中,我們便可以定義S(x)=x?+x?,此時滑模系數矩陣 C=[11]?。
在定義好滑模面S(x)之后,我們只需要確定滑模控制器的滑動模態方式以及趨近率方式,即可確定控制輸入 u。我們希望系統能夠在任何的外部干擾作用下,質量滑塊都能沿著滑模面穩定在原點附近,所以我們選擇“調節模式”作為滑動模態方式,并選擇指數速率作為趨近率。
當然這些設置在 MATLAB 中都非常容易實現,只需要在 Sliding ModeController (Reaching Law) 模塊的對應位置給定參數即可。
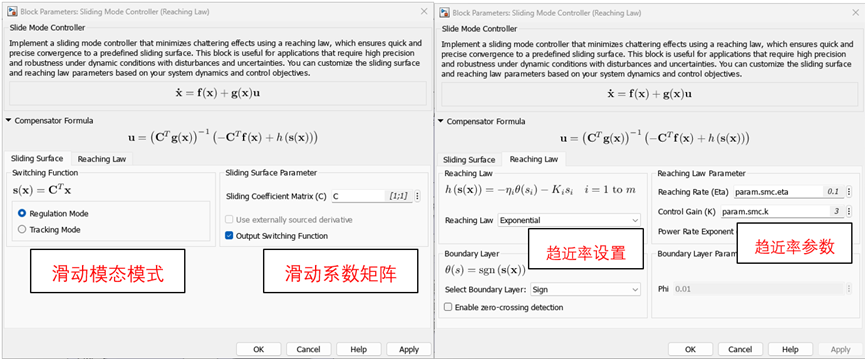
圖5Simulink SMC 模塊設置
我們希望控制器能在系統存在外部輸入干擾的情況下,讓質量滑塊穩定在原點,建立如下 Simulink 模型來查看仿真結果。
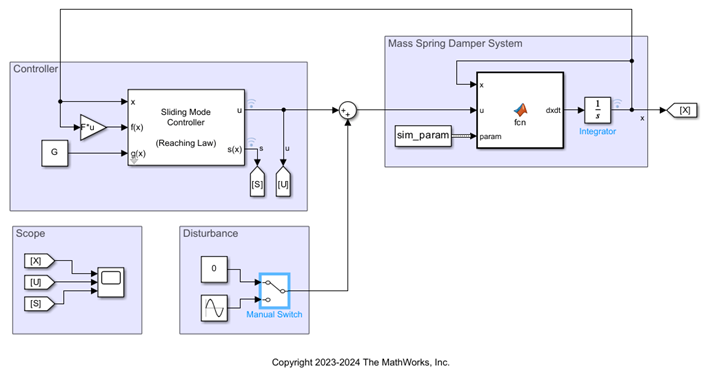
圖6Simulink SMC閉環模型
在圖5 的 SMC 模塊設置中,除了我們已經介紹過的參數,還出現了一個參數叫做“Boundary Layer”,這就涉及到滑模控制的一大缺點-“顫振”。還是考慮圖4所示的滑模面,滑模控制的理想情況是當系統狀態到達滑模面時,不再離開滑模面,沿著其移動。但在實際物理系統中,“誤差”不可避免地存在,所以實際上系統狀態在到達滑模面時,并不“嚴格”沿著其移動,而會在其附近“來回晃動”(如圖中藍色折現所示)。
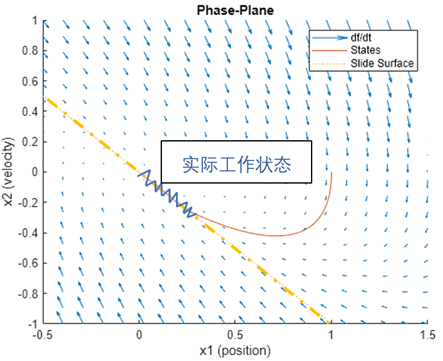
圖7 滑模面實際工況示例
我們在一開始概述的時候講到,滑模控制與常規控制的區別在于控制的不連續性,其在滑模面兩邊的控制輸入完全不同,在滑模面附近晃動會使得系統的控制輸入呈現“高頻開關”的狀態,從而導致“顫振”現象的發生。
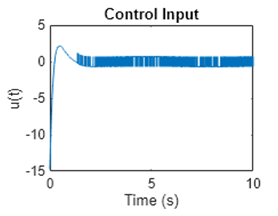
圖8SMC控制輸入“顫振”現象
為了防止這種現象的發生,我們需要設定一個合理的“邊界”,當系統的狀態沒有偏離滑模面到邊界值時,視為其仍然在滑模面上,不做控制輸入的切換,實現一定程度上的“滯回”作用(如圖中虛線所示)。
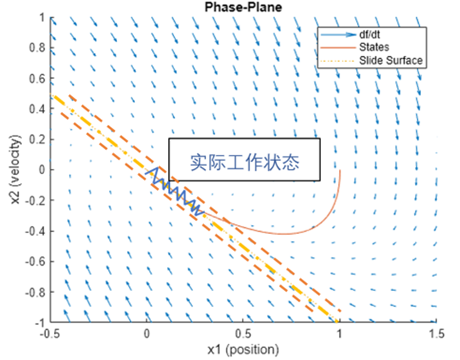
圖9SMC 模塊中Boundary Layer的設定意義
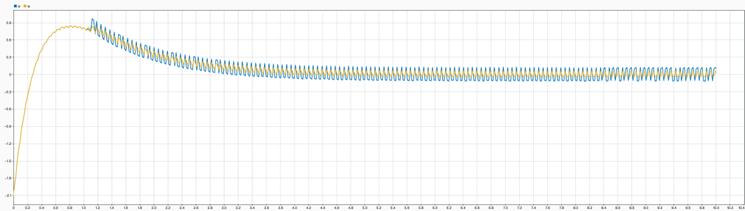
圖10 不同Boundary Layer 參數下的輸入顫振對比
典型案例分析之二變參數機械臂控制
現實世界中的真實物理系統當然遠比上述的質量-彈簧-阻尼系統復雜得多,外部干擾對系統本身的影響也大得多。簡單的被控對象可以幫我們充分理解滑模控制的原理以及優缺點,并幫助我們應用在更加貼近物理實際的場景當中。在 24b 的幫助文檔中,還內置了另外一個更加復雜的 SMC 機械臂應用案例,SlidingMode Control Design for a Robotic Manipulator [3]。
示例中,我們考慮帶有兩個關節的機械臂,并且其本身的動態特性(狀態方程中的矩陣參數)與標稱值是有偏移的,當下圖中機械臂狀態矩陣的估計器(Estimator)無法準確估計真實的機械臂系統時,SMC暫展示出了良好的控制性能,能夠應對系統中的未知干擾與不確定性。
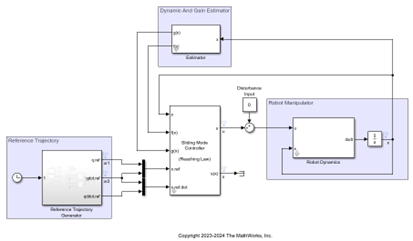
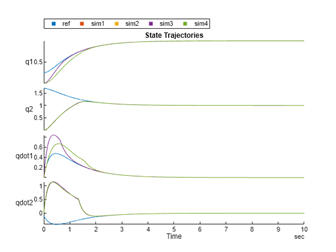
圖11 機械臂滑模控制示例
因為篇幅的關系,此案例就不作詳細介紹了,各位可以參閱幫助文檔鏈接,在軟件中打開模型進一步研究。
寫在最后
MathWorks 在近些年來的版本中持續關注著廣大用戶對于非線性控制的需求,陸續添加了許多“即插即用”的控制算法模塊(如前文提到的自控擾控制、模型參數自適應控制、極值搜索控制、模型預測控制等等),使得控制工程師們不必糾結于如何用代碼實現相對成熟的控制理論本身,而是把精力更多地放在充分了解自身的被控物理對象特性,有理有據地調節控制算法中的參數,從而快速實現并基于自動代碼生成無縫部署到嵌入式硬件中。
除了本文提到的滑模控制,在新版本中,MATLAB/Simulink 還發布了迭代學習控制(Iterative LearningControl, ILC)模塊,幫助有需要的用戶快速實現并部署該算法。 我們也樂于聽到大家的心聲,如果您有更多關于先進控制算法的使用需求和場景,不妨通過留言告訴我們,幫助 MATLAB/Simulink 持續提升!
-
matlab
+關注
關注
185文章
2974瀏覽量
230382 -
機器人
+關注
關注
211文章
28379瀏覽量
206913 -
Simulink
+關注
關注
22文章
533瀏覽量
62378 -
航空航天
+關注
關注
1文章
387瀏覽量
24271
原文標題:高效應對“外部干擾與非線性” - Simulink 滑模控制(SMC)更新探討
文章出處:【微信號:MATLAB,微信公眾號:MATLAB】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
PMSM在Simulink下的FOC滑模速度環仿真
IPMSM調速系統滑模變結構控制

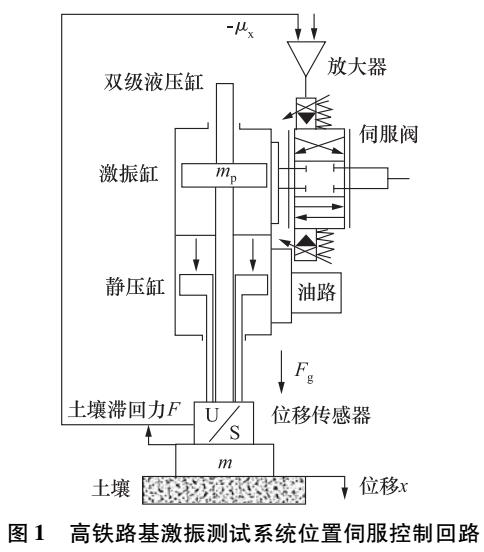
激振測試系統滑模控制特性分析




 Simulink滑模控制原理概述
Simulink滑模控制原理概述











評論