我想大家都有這樣的體會:小學的時候你根本不知道初中數學是什么樣,高中的時候你也根本想不到大學數學是什么樣。而大學生,如果你不專注于數學,恐怕也不知道現代數學是什么模樣。下面將分別從學數學的動機、數學不同學科的分類以及如何切實可行培養數學能力等幾個方面闡述如何學習數學。
進入正題:
一、認清你的需要
為什么需要學習數學,這是你首先需要想清楚的問題。數學學科子分類多、每一本數學書中都有許多定理和結論,需要花大量時間研究。而人的時間是寶貴的、有限的,需不需要學數學,學數學到什么程度你需要大體有一個目標和計劃,合理安排時間。
1.1你的目標是精通數學、鉆研數學,以數學謀生,你可能立志掌握代數幾何,或者想精通前沿物理。那么你需要打下堅實的現代代數、幾何以及分析基礎,你需要準備大量時間和精力,擁有堅定不移的決心。(要求:精通全部三級高等數學)
1.2你的目標是能夠熟練運用高等數學,解決問題,掌握探索新應用領域的武器,你可能立志進入計算機視覺領域、經濟學領域或數據挖掘領域。那么,你需要打下堅實的矩陣論、微積分以及概率統計基礎。(要求:精通第一級高等數學)
1.3你的目標是想了解數學的樂趣,把學數學作為人生一大業余愛好。那么,你需要打下堅實的線性代數、數學分析、拓撲學以及概率統計基礎,對你來說,體會學數學的樂趣是一個更重要的目標。(精通第一級高等數學,在第二級高等數學中暢游,嘗試接觸第三級高等數學)
二、給自己足夠的動力
學數學需要智力,更需要時間和精力。下面的幾個事實相大家都深有體會:
1.凡是沒有用的東西,或者雖然有用,但是你用不到的東西,學得快忘得也快。不信你回憶一下你大一或者初一的基礎課,你還記的清楚嗎?
2.凡是你不感興趣(或者感覺不到樂趣)的東西,你很難堅持完成它。很多人都有這樣的經歷,一本書,前三章看的很仔細,后面就囫圇吞棗,越看越快,反正既沒意思也沒用。
3.小學數學是中學數學的基礎,中學數學是高中數學的基礎,高中數學是大學數學的基礎(你可以以此類推)。因此,無論你的目標是什么,搞數學、用數學、還是體會數學的樂趣、滿足自己從少年時就有的夢想。學有所樂、學有所用,永遠是維持你動力不衰退的兩個最主要的因素。
三、如何學習現代數學
首先我們要知道什么是數學,要對數學下個定義是很難的。本文的處理途徑是,不去回答它,我不打算給出數學的定義而是通過描述它的許多最重要的概念,定理,和應用使對于什么是數學有一個好的看法,而要使這些有意義對數學進行分類是很有必要的
1現代數學可以大致被分為兩個領域:純粹數學(研究數學本身)和應用數學(用以解決更實際的問題)。但我們要記住的是,它們之間其實有著緊密的關聯。如果能的話,應該畫張圖更好一點,地圖更應該是一張網絡,連接著每個相關的分支。
事實上,從歷史中我們會發現,有許多數學家一開始只是出于好奇以及對美的追求去研究數學,然后發展了一系列美麗而又有趣的數學分支,但對于真實世界卻一點用處都沒有。令人驚喜的是,比如在100年后,當有些科學家正在試圖解決物理學或計算機科學最前沿的問題時發現,他們所需要的數學其實早就在純粹數學里被發展出來了。這樣的例子不勝枚舉,比如廣義相對論的發展依賴于黎曼度規;弦理論則需要卡-丘空間等等。這些抽象的概念最終被應用在其它的科學領域中是非常令人欣喜的一件事。先拋開純粹數學是否有一天能被應用在現實中去,其實研究純粹數學本身也是非常有價值的事。如果你問一位數學家為什么要研究純粹數學,我想很多人的答案會簡潔到只有一個字,那就是:美!
2.純粹數學
純粹數學主要包括四個部分:數字系統、結構、空間和變化。
2.1【數字系統】
數字系統的研究起源于數,一開始為熟悉的自然數(1、2、3...)及整數(…-2、-1、0、1、2...)與被描述在算術內的自然數及整數的算術運算(+-× ÷)。當數系進一步發展時,整數被視為有理數(-7、1/2、2.32...)的子集,而有理數則包含于實數(-4π、e、√2...)中。實數則可以進一步被廣義化為復數(4+3i、-4i...)。除此外,還有其它一系列的數(比如四元數、八元數和基數等)。還有一些數深受數學家的喜愛,比如π、e和質數(1,3,11...)。
剛才提到的這些數字都有一些有意思的性質,例如,盡管實數和整數都有無限多,但實數要比整數多。所以有一些無限實際要比另一些大。
2.2【結構】
對結構的研究起始于將數字以變量的形式代入方程(y=mx+c)。如何解這些方程的規則包含在代數之中。在這個分支中,還有矢量和矩陣,它們都是多維數,而它們之間的聯系于線性代數中被研究。
在這個分支內,有一個被譽為“最純”的數學領域,那就是數論。數論專注于研究在“數字系統”中提到的所有數的特征,比如質數的性質(質數產生了很多非專業人士也能理解而又懸而未解的問題,如哥德巴赫猜想,孿生質數猜想等)。
另一方面,組合數學是一門研究可數或離散對象的數學分支,比如樹、圖論等,一些著名的問題包括地圖著色問題、船夫過河問題等等。群論則是研究名為群的代數結構,一個熟悉的例子就是魔方,是一個置換群。序理論是研究捕獲數學排序的直覺概念的各種二元關系的數學分支,比如哈斯圖,是用來表示有限偏序集的一種數學圖標。
2.3【空間】
純粹數學的另一個部分是研究形狀和它們在空間中的行為。空間的研究源自于幾何——尤其是歐幾里得幾何。三角學則結合了空間及數,且包含有著名的勾股定理。還有一些比較有趣的領域,比如分形,它是一種具有尺度不變性的數學模式,意思是說你無論你怎么放大它們看起來都是一樣的。
在其許多分支中,拓撲學可能是20世紀數學中有著最大進展的領域。拓撲學研究的是空間的不同性質,你可以連續不斷地將它們變形,但不能將它們撕裂或粘合。例如,無論你對莫比烏斯帶做什么,它永遠只有一個面和一個邊界。在拓撲學里,咖啡杯和甜甜圈是一樣的東西。拓撲學包含了存在已久的龐加萊猜想(2006年由數學家格里戈里·佩雷爾曼證明)以及頗有爭議的四色定理(1976年由計算機證明)。
測度論是一種給空間或集分配數值的數學分支,它將數和空間聯系起來。最后,微分幾何是非常重要的一個數學分支,它研究在彎曲表面上的形狀的性質,比如三角形在彎曲的表面中內角和跟在歐式空間中的不一樣。
2.4【變化】
了解及描述變化在自然科學里是一個普遍的議題,而微積分更加使研究變化的有力工具。函數誕生于此,作為描述一變化的量的核心概念。微積分是研究極限、微分學(函數的梯度的行為)、積分學(函數下的面積)和無窮級數的一個分支。而向量分析關注的則是向量場的微分和積分。除此外,還有一系列其它的研究方向。動力系統描述的是系統如何隨著時間流逝從一個狀態演化到另一個狀態,比如流體流動或任何有反饋環路的東西(如生態系統)。混沌理論則是對系統的既不可預測而又是決定的行為作明確的描述,它對于初始條件非常敏感,比如著名的蝴蝶效應。最后是復分析,對于實數及實變函數的嚴格研究為實分析,而復分析則為復數的等價領域。數學中最大的未解問題之一——黎曼猜想便是以復分析來描述的。
以上這些便是純粹數學的各個分支。接下來我們進入應用數學的領域。應用數學的主旨在于將抽象的數學工具運用在解答科學、工程、商業及其他領域上的現實問題。
3.應用數學
數學被廣泛地應用在各個科學領域。
3.1我們從物理學開始。基本上在純粹數學提到的所有分支都多多少少的被應用于物理學上。數學和理論物理跟純粹數學的關系是密不可分的。許多數學理論是在物理問題的基礎上發展起來的;也有很多數學方法和工具通常只在物理學中找到實際應用。例如,微分方程被應用在經典力學和量子力學;場論被應用在電磁場、引力場和規范場;群論和表示論別應用在粒子物理學中。
3.2除了物理外,數學也被應用在其它的自然科學上,特別是在數學化學和生物數學上。在數學化學中,數學模型通常被用以模擬分子;拓撲化學也是一個熱門的研究領域(2016年的諾貝爾化學獎就跟拓撲有關)。數學也大量應用在生物學中,如由于基因學的發展,生物學家采集到的大量數據必須通過解析方法加以處理;演化生物學和生態學都大量使用數學理論等等。
3.3數學也被大量應用在工程學上,自古埃及和巴比倫時期,數學就被大量應用在建筑上。非常復雜的電路系統,比如在飛機或電網中,就利用了動力系統的方法,叫控制理論。
(這里推薦一本Mary Boas寫的教材《Mathematical Methods in the Physical Sciences》,對于那些本科選擇物理、化學和工程專業的學生,這本書可以快速的幫你們掌握所需要的數學知識。)
3.4當一些數學太過于復雜我們無法有效地解決時,我們就會用到數值分析,它也包含了對計算中舍入誤差或其它來源的誤差之研究。例如,如果你把一個圓圈放進一個正方形中,并向它扔許多的飛鏢,接著比較飛鏢在圓圈和正方形的數量,你就可以得到π的近似值。但在現實中,數值分析通常會使用大型計算機來實現。
3.5博弈論專注于思考游戲中的個體的預測行為和實際行為,并研究它們的優化策略。主要研究公式化了的激勵結構(游戲)間的相互作用。其中一個代表性的應用例子是囚徒困境。博弈論在經濟學、心理學、生物學、國際關系、政治學等其它學科都有廣泛的應用。
3.6概率論是集中研究概率及隨機現象的數學分支,最簡單的隨機事件為扔硬幣、抽撲克或擲骰子。應用數學中的一個重要領域為統計學,它利用概率論為其工具并允許對含有機會成分的現象進行描述、分析與預測。大部分的實驗、調查及觀察研究都依賴于統計分析。因此被廣泛地應用在各門學科,從自然科學、社會科學到人文學科。特別是在金融行業,通過統計分析以獲取最大的利益。
3.7跟最大化利益相關的是最優化,你試圖計算的是在一系列不同選擇或限制下的最佳選擇,也就是找到一個函數的最高或最低點。最優化問題是人類的第二天性,我們一直在都在進行最優化選擇,比如試圖最優化我們的快樂程度,購買的時候想要物有所值等等。
3.8另一個領域跟純數學有非常深的聯系,那就是計算機科學。計算機科學的規則事實上是從純數學中推導出來的。機器學習是實現人工智能的一個途徑,即以機器學習為手段解決人工智能中的問題。機器學習是一門多領域的交叉學科,利用了數學的許多領域,比如線性代數、最優化、動力系統和概率論等等。
3.9最后,密碼術也是非常重要且實用的一個數學分支,應用到了純粹數學研究,比如組合數學和數論等。
現在我們已經概括了純粹數學和應用數學的主要部分。但是,還沒有結束,我們不能夠忽略數學的基礎。
4.基礎
數學的基礎試圖理解數學本身的性質,并且追問所有數學規則的基礎是什么。是否存在著一套稱為公理的完整的基本規則?我們要如何證明它是否自洽?數理邏輯、集合論和范疇論就試圖回答這個問題。在數理邏輯中有一個非常著名的成果叫做哥德爾不完備定理,對大多數人來說,數學并沒有一套完整和自洽的公理,意味著它們都是由我們人類創造的。這聽起來很奇怪,因為數學如此完美的解釋了宇宙中的許多事物。為什么我們會認為由人類創造的東西可以做到如此地步?這是一個非常深奧的謎題。我們還有計算理論,它專注于研究不同的計算模型,基于這些模型如何能夠有效地解決問題。它包含了復雜性理論,其中P/NP問題是該領域中至今沒有解決的問題。數學是一個非常抽象和美妙的世界,如果要用一句話形容它的重要性,那么我會選擇伽利略曾經說過的:“如果一個人不懂得宇宙的語言,即數學的語言,他就不能夠閱讀宇宙這本偉大的書。”
四、如何學習
4.1適量做題
千萬千萬千萬不要狂做題。比如說你先花5年做完吉米諾維奇六本數學分析習題集,那么到時候你就30歲了,后面的二級課程還沒開始學呢。因此,做一些課后習題,幫助你復習、思考、維持大腦運轉就行,要不斷地向后學。如果完全學不懂了,返回來做習題幫自己理清頭緒。
4.2了解思想
數學的精髓不是做題的數量,而是掌握思想。每一個數學分支都有自己的主線思想和方法論,不同分支也有相互可供對比和借鑒的思維方式。留意它,模仿它,瑣碎的知識就串成了一條項鏈,你也就掌握了一門課。思想并不是讀一本教材就能輕易了解的,你要讀好幾本書,了解一些應用才能體會。舉兩個例子:
微積分的主線有這么幾條:認識到微觀和宏觀是有聯系的,微分用來刻畫事物如何變化,它把細節放大給你看,而積分用來刻畫事物的整體性質;微分和積分有時是描述一個現象的不同方式,這一點你在數學分析書中可能不容易發現,但是如果學點物理,就會發現麥克斯韋方程組同時有等價的微分形式和積分形式;積分變換能夠建立不同空間之間的的聯系,建立空間和空間邊界的聯系,這就是Stokes定理,這個公式最遲要在微分流形中你才能一窺全貌。
矩陣是空間中線性變換的抽象,線性代數這門課的全部意義在于研究如何表達、化簡、分類空間線性變換算子;SVD分解不僅在應用學科用有極為廣泛的亮相,也是你理解矩陣的有力工具;矩陣是有限維空間上的線性算子,對"空間"的理解不僅能讓你重新認識矩陣,更為泛函分析的學習開了個好頭。
4.3漸進式迂回式學習,對比學習
很多時候,只讀一本書,可能由于作者在某處思維跳躍了一下,以后你就再也跟不上了。學習數學的一個訣竅,就是你同時拿到好幾本國際知名教材,相互對比著看,或者看完一本然后再看同一主題的另一本書,已經熟悉的內容跳過去,如果看不懂了,停下來思考或者做做習題,還是不懂則往后退一退,從能看懂的部分向前推進,當你看的多了,就會發現一個東西出現在很多地方,對它的理解就加深了。舉兩個例子:
a.外微分這個東西,國內有的數學分析書里可能不介紹,我第一次遇到是在彭家貴的《微分幾何》里,覺得這是個方便巧妙的工具;后來讀卓里奇的《數學分析》和Rudin的《數學分析原理》,都講了這個東西,可見在西方外微分是一個基礎知識。你要讀懂它,可能要首先理解矩陣,明白行列式恰好是空間體積在矩陣的變換下拉伸的倍數,它是一種線性形式。最后,當你讀微分流形后,將發現外微分是獲得流形上的Stokes定理的工具。
b.點集拓撲學這個東西,搞應用用不到。但是但凡你想往深處學,這一門學科就必須要掌握,因為它提供對諸如開集、緊集、連續、完備等數學基本概念的精準刻畫。往后學泛函分析、微分流形,沒有這些概念你將寸步難行。首先你要讀芒克里斯的曠世名著《拓撲學》,接著在讀其他外國人寫的書時,或多或少都會接觸一些相關概念,你的理解就加深了,比如讀Rudin的《泛函分析》,開始就是介紹線性拓撲空間,前面的知識你就能用上了。
4.4建立不同學科的聯系
看到一個東西在很多地方用,你對它的理解就加深了,慢慢也就能體會到這個東西的精妙,最后你會發現所有的基礎學科相互交織,又在后續應用中相互幫助,切實體會到它們真的很基礎,很有用。這是一種體會數學樂趣的途徑。
4.5關注應用學科(上文介紹過一些)
沒有什么比應用更能激發你對新知識、新工具的渴望。找一些感興趣的應用學科教材,讀一讀,開闊眼界,為自己的未來積累資源。以下結合自己的專業(計算機視覺)和愛好說說一些優秀的專業書籍:
學了微積分,就可以無壓力閱讀《費恩曼物理學講義第一卷》,了解力、熱、光、時空的奧秘;學了偏微分方程,就可以無壓力閱讀《費恩曼物理學講義第二卷》,了解電的奧秘;學了矩陣論,可以買一本《計算機視覺中的多視圖幾何》,了解成像的奧秘,編程進行圖像序列的三維重建;學了概率論的同學應該會聽說過貝葉斯學派和頻率學派,這兩個學派的人把戰場拉到了機器學習領域,成就了兩本經典著作《Pattern Recognition And Machine Learning》和《TheElements of Statistical Learning》,讀了它們,我被基礎數學為機器學習領域提供的豐碩成果和深刻見解深深折服;讀了《Ray Tracing from the Ground Up》,自己寫了一個光線追蹤器渲染真實場景,它的基礎就是一點點微積分和矩陣......
高等數學的應用實在是太多了,如果你喜歡編程,自動化、機器人、計算機視覺、模式識別、數據挖掘、圖形圖像、信息論和密碼學......到處都有大量模型供你玩耍,而且只需要一點點高等數學。在這些領域,你可能能發現比數學書更有趣,也更容易找到工作的目標。
4.6找有趣的書看
數學家寫的書有時是比較死板的,但是總有一些教材,它們的作者有強烈的欲望想向你展示"這個東西其實很有趣","這個東西完全不是你想的那個樣子"等等,他們成功了;還有些作者,他們喜歡把一個東西在不同領域的應用,和不同東西在某一領域的應用集中展示給你看。這樣的書會提供給你充足的樂趣讀下去。典型代表就是國內出版的一套《圖靈數學統計學叢書》,這一套書實在是太棒了,比如《線性代數應該這樣學》《復分析:可視化方法》《微分方程、動力系統與混沌導論》,個人認為都是學數學必讀的經典教材,非常非常有趣。
五、多讀書,讀好書
如果只有一句話概括如何培養數學能力,那么就是這一句:多讀書,讀好書。因此這一步我想單獨拿出來多說兩句。
想必大家都十分精通并能熟練應用小學數學。想讀懂代數幾何,或者退一步,想讀懂信息論基礎,你就要挑幾本好的基礎教材,最好是外國人寫的,像掌握小學數學那樣掌握它。不要只看一本,找三本不同作者的書,對比著看,逐行逐字看。有的地方肯定看不懂,記下來,說不定在另一本書的某個地方就從另一個角度說到了這個東西。
如果你以后還要往后學,現在看到的每一個基礎定理,以后還會用到。每一本基礎書,你今天放棄,明天還要乖乖重頭再來。要像讀經文一樣,交叉閱讀對比不同教材內容的異同。
-
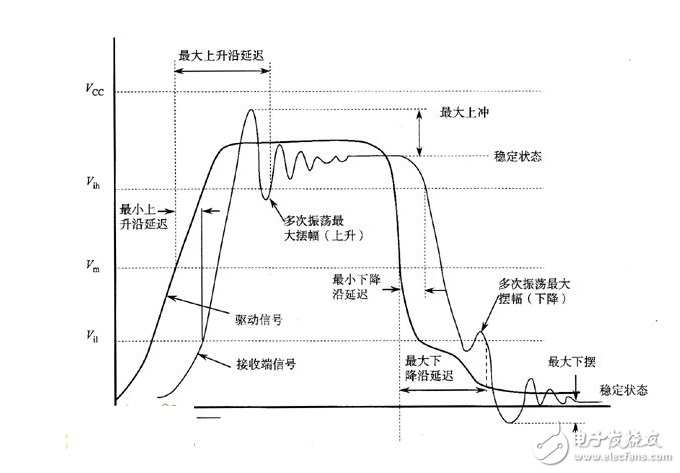
信號完整性
+關注
關注
68文章
1408瀏覽量
95496
原文標題:【充電】如何學好數學----轉給信號完整性工程師看看
文章出處:【微信號:SI_PI_EMC,微信公眾號:信號完整性】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




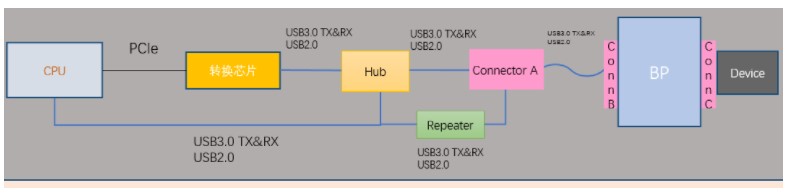
 學好數學幫工程師做信號完整性設計
學好數學幫工程師做信號完整性設計










評論