1 引言
永磁同步電機具有結構簡單、體積小、效率高、損耗小和功率體積比大等優點,目前被廣泛應用于新能源汽車的驅動系統。電機作為驅動系統電磁干擾流經的重要路徑,建立其高頻模型,對下一步搭建系統整體的傳導干擾和輻射干擾預測模型十分重要,因此,電機高頻模型的精度和準確度會對系統整體模型的精確性和正確性產生很大影響。然而,目前用于建立電機高頻模型的方法往往存在建模過程復雜、誤差大、通用性差及模型頻帶覆蓋窄等問題,因此,需要一種更為有效的建模方法。
本文首先介紹基于矢量匹配法的電路建模方法:闡述矢量匹配法的基本原理,描述高頻等效電路構建過程,推導其模型參數的計算方法。隨后用此方法建立星形和三角形兩種不同接線方式的永磁同步電機高頻電路模型,并進行實驗驗證。
2 矢量匹配法
2.1概述
矢量匹配法(Vector Fitting)[1]是Gusavsen和Semlyen于1999年提出的一種穩定、有效的擬合方法,該方法避免了有理逼近過程中出現的病態和不平衡加權問題,目前廣泛應用于電力系統和高速電路設備頻率特性擬合[2-4],矢量匹配法特別適用于有關頻變效應的建模,并在擬合過程中表現出良好的魯棒性、有效性和穩定性。
2.2矢量匹配法基本原理
電網絡理論中,線性電路的網絡函數可表達為一有理函數:
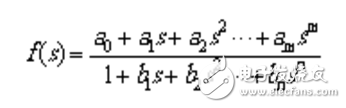
(1.1)
可將此函數寫成極點、留數形式,即
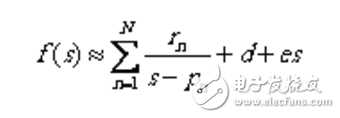
(1.2)
其中,留數和極點是實數或共軛復數對,d和e是實數。
① 矢量匹配法求解過程
給定一組測試數據 (k=1,2…。.P),當極點給定時,式(1.2)就變成關于待求參數、d和e的線性函數,采用矢量匹配法可解出式(3.2)中所有參數、、d和e,其求解過程如下:
設(n=1,2…。.N)是函數給定的一組初始極點,同時引入輔助函數,將與相乘,假設與有相同的極點,可得方程:
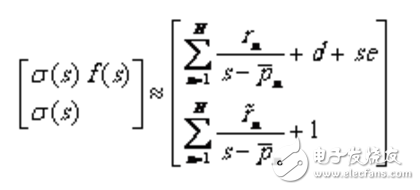
(1.3)
在上式中,有理函數和近似式具有相同的極點,是未知函數的留數,此外,函數的項被強制為1。將式(1.3)中第二行兩端同乘并與第一行進行減法運算,可得關于待求參數、、d和e的線性方程。
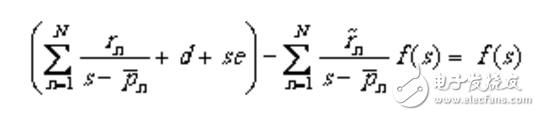
(1.4)
將一組測試數據(k=1,2,3…P)及其對應頻點代入(1.4)式,可得一組線性方程,其矩陣形式為
(1.5)
其中,系數矩陣的第k行元素為:

(1.6)
解向量x和已知向量b分別為:
(1.7) (1.8)
假設第和極點或留數為一組共軛復數對時,形式如下:
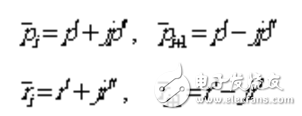
(1.9)
則矩陣中對應元素為:

(1.10)
此時矩陣相應的留數分別是和。
對于式(1.5)一般有,因此它是超定的,可以用最小二乘法求解得到、、和。但是,由給定的初始極點求解式(1.5)計算得到的、和并不準確,因此需要修正初始極點,求解下一次迭代過程中的初始值,使逐步逼近。
用表示式(1.3)第一個方程的右邊,將和寫成零極點形式有

(1.11)

(1.12)
式中,和分別是和的零點。由上式可得
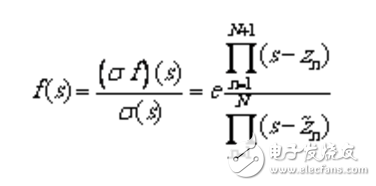
(1.13)
上式表明,的極點與的零點相等。由于有理函數和具有相同的極點,這樣,初始極點在運算的過程中相互抵消,求解得到的零點就是下一次迭代的極點。
由式(1.3)和(1.12)可得:
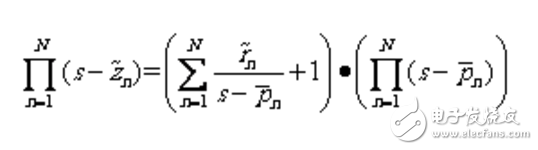
(1.14)
將上式右側寫為行列式形式有
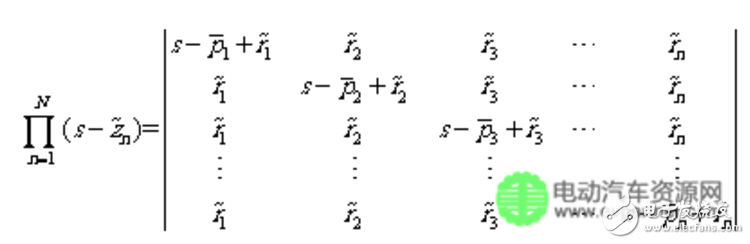
(1.15)
構建矩陣
(1.16)
式中,是包含初始極點的對角矩陣,是元素為1的列向量,是包含留數的行向量,即

(1.17) (1.18)
因此矩陣的特征多項式就是式(1.15),由此,的零點可通過求解矩陣的特征值得到。
當中極點和中對應留數是共軛復數時,各矩陣相應部分的子矩陣為
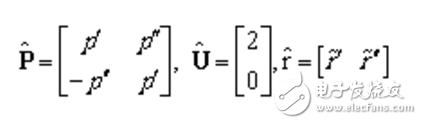
(1.19)
將計算得到的特征值替代式(3.4)的給定的初始極點,再求解式(1.5)。重復這一迭代過程數次,最后得到滿足精度要求的和。
3 永磁同步電機高頻建模
對三相永磁同步電機進行高頻建模,本文采用測量法,即把電機看成一個“黑盒子”,不需要知道電機結構和電磁參數,只需測量電機端部阻抗頻譜特性,結合矢量匹配法,即可模擬出電機高頻電路模型。
電動汽車使用的電機的定子繞組接線方式有兩種:星形和三角形,根據電機繞組的連接方式不同,分別對星形接線和三角形接線的永磁同步電機進行高頻建模。需要強調的是,在矢量法建模過程中,取為阻抗參數還是導納參數與定子繞組的接線方式無關,這兩個參數是可以相互轉換的。
3.1三角形接線電機建模
目前,針對永磁同步電機高頻模型研究對象大多數為星形聯結的電機,而對定子繞組為三角形聯結的電機研究很少。通常,大功率電機的定子繞組接線方式采用三角形聯結,這是因為在相同功率下三角形接線較星形接線下繞組中流過的電流較小,可以使繞組線圈制造和布線更為方便。而采用將三角形電機繞組拆卸獲取電路參數的方法通用性差,提取過程復雜。因此,有必要對三角形聯結的電機高頻模型進行研究。
①電機模型
圖1三角形接線電機模型
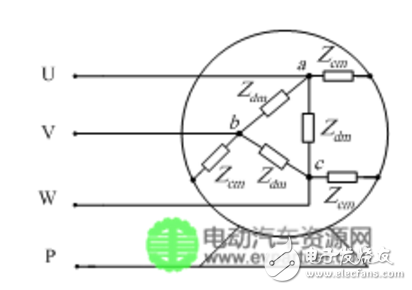
三角形接線電機的高頻阻抗網絡模型如圖1所示,圖中,表示三相繞組對地的阻抗,為共模阻抗,表示三相繞組之間的差模阻抗。永磁同步電機的轉子是永磁體,忽略其渦流損耗和磁飽和效應,因此在建模中同樣沒考慮轉子的影響。
② 抗測量
電機阻抗測量采用共模和差模測量兩種方式,測試設備Agilent4294A,測試頻段為100kHz-100MHz,測試頻點數201個。共模測量即測試電機三端口并聯后和機殼間的阻抗,其測試阻抗表示為,如圖2所示;差模測量即測試電機兩端口并聯后和第三端口間的阻抗,其測試阻抗表示為,如圖3所示。
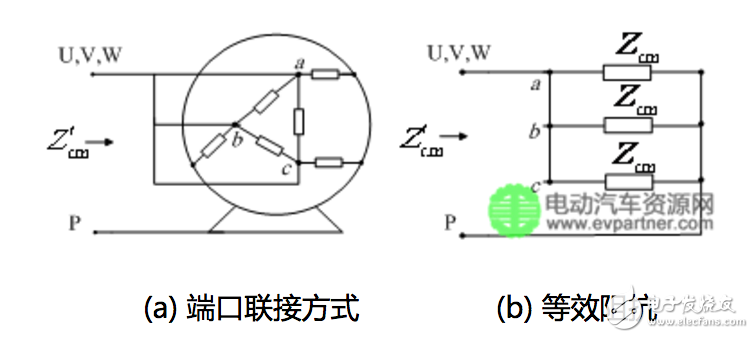
(a) 端口聯接方式 (b) 等效阻抗
(a) Motor terminal connections (b) Motor equivalent impedance
圖2共模阻抗
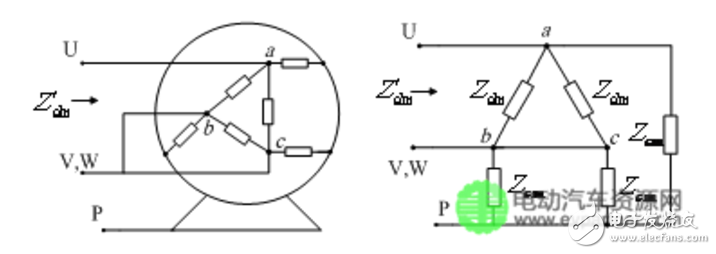
(a) 端口聯接方式 (b) 等效阻抗
(a) Motor terminal connections (b) Motor equivalent impedance
圖3差模阻抗
③數據處理
根據圖2(b)和2(b),測量阻抗和與繞組阻抗和的關系為:

(1.20)
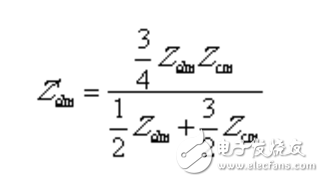
(1.21
通過式(1.20)和(1.21)可以求得繞組阻抗和的表達式:
(1.22)
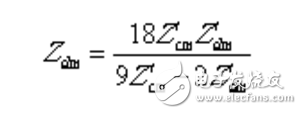
(1.23)
上節在建立星形聯結電機建模過程中,使用了基于阻抗函數的矢量匹配法,本節將采用基于導納函數的矢量匹配法擬合其等效電路。在此以求解的等效電路為例說明求解的整個過程。
表1 的矢量匹配法求解參數
Table.1 VF method for
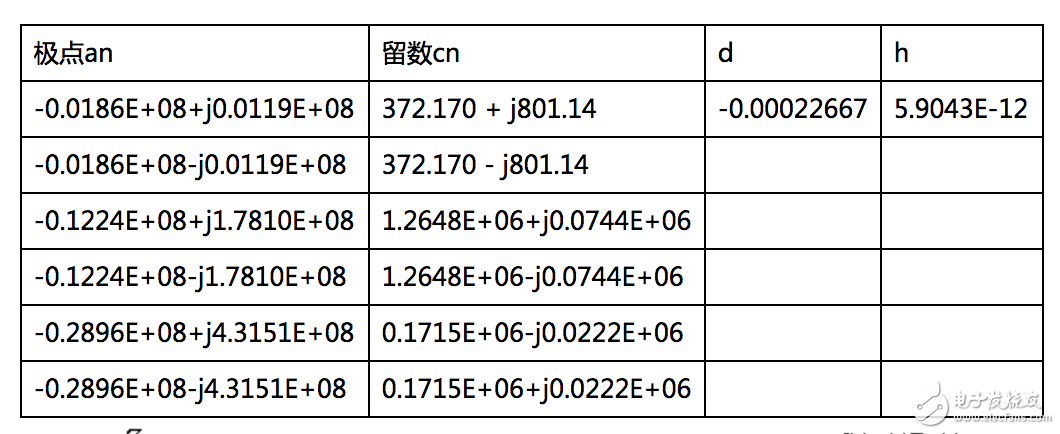
通過式(1.23)可得的阻抗特性數據,將獲得的阻抗數據轉換為導納,即后,代入矢量匹配法程序,進行6階擬合,得到導納函數的極點和留數,如表1所示。
在Saber搭建阻抗和的等效電路模型,和的仿真與實測結果對比如圖4所示。由圖可知,用基于導納函數的矢量匹配法擬合得到的電路參數能很好的吻合待建模阻抗的高頻特性。在求解求解和等效電路的過程中,原始數據中包含的阻抗的實部、虛步信息,其仿真數據在幅值和相位上都有很好的擬合效果。
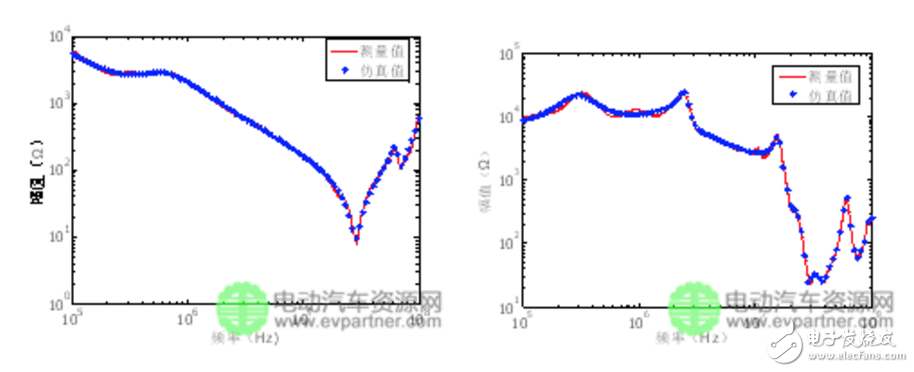
(a) 繞組共模阻抗 (b) 繞組差模阻抗
(a)The winding CM impedance (b) The winding DM impedance
圖4 阻抗對比
③ 模型驗證
將得到的和等效電路按圖1的連接方式在Saber軟件中搭建電機EMI高頻模型。計算和在100 kHz~100 MHz的阻抗特性曲線,并與實際測量結果進行對比。阻抗曲線仿真和實測對比如圖5、6所示,對比可以發現,測量阻抗的幅頻特性和相頻特性與仿真結果在整個頻段范圍內曲線吻合很好,進一步驗證了矢量匹配法的正確性和準確性。
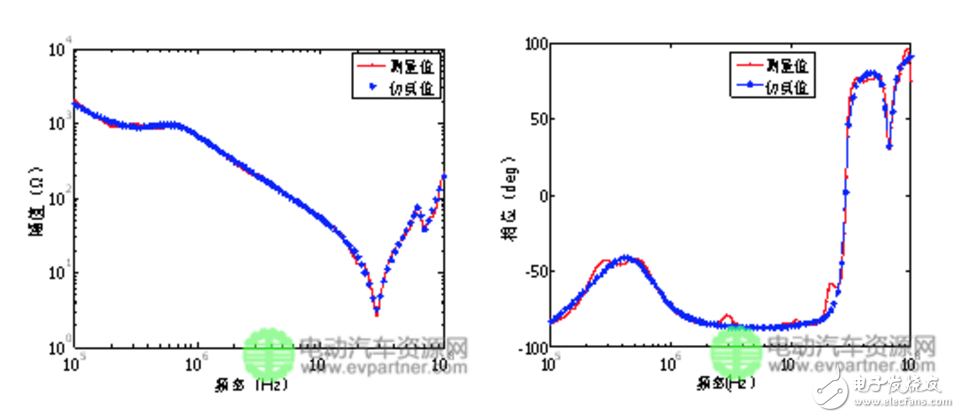
(a) 幅值 (b) 相位
(a) Amplitude (b) Phase
圖5 仿真與實測結果
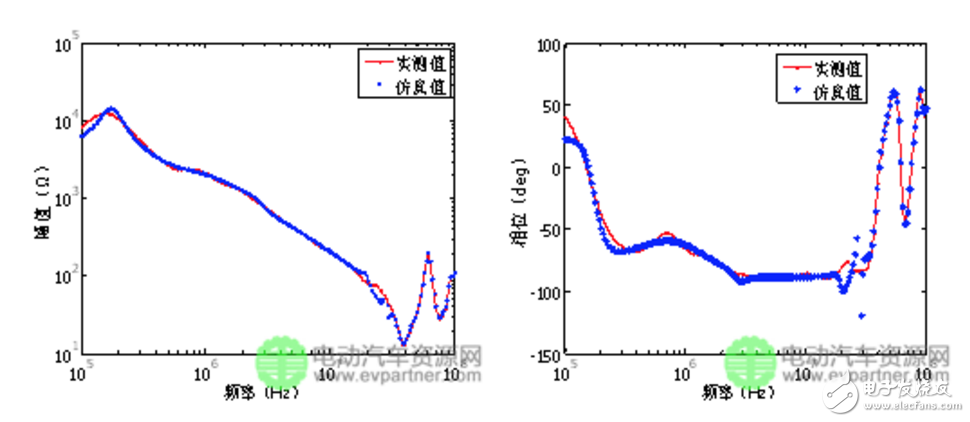
(a) 幅值 (b) 相位
(a) Amplitude (b) Phase
圖6 仿真與實測結果
4 小結
本文研究了建立永磁同步電機高頻電路模型的方法。介紹了矢量匹配法的基本原理,通過對網絡函數極點和留數等參數的分析,分別推導出基于阻抗函數和導納函數的等效電路建立過程,并應用于三角形聯結的永磁同步電機高頻電路的建模。永磁同步電機的建模過程歸納為:構建電機繞組高頻模型的電路拓撲,通過共模測量和差模測量獲得模型中共模阻抗和差模阻抗的頻率特性;使用矢量匹配法將測試數據進行處理,計算阻抗(導納)函數的極點留數等參數,隨后轉換為相應的等效電路。電機高頻電路模型的時頻域仿真結果和實測數據的對比,驗證了利用矢量匹配法建立永磁同步電機高頻模型的正確性和有效性。此外,該建模思路和方法同樣可以用于其他種類的交流電機高頻電路模型,具有一定的通用性。本研究內容為研究電機驅動傳導電磁干擾和輻射電磁干擾問題打下基礎,對建立驅動系統精確的傳導和輻射干擾模型有重要意義。
-
永磁同步電機
+關注
關注
28文章
875瀏覽量
49920 -
高頻電路
+關注
關注
12文章
235瀏覽量
35967
發布評論請先 登錄
相關推薦
太實用!永磁同步電機控制方案及MATLAB仿真模型大全
永磁同步電機HIL仿真系統
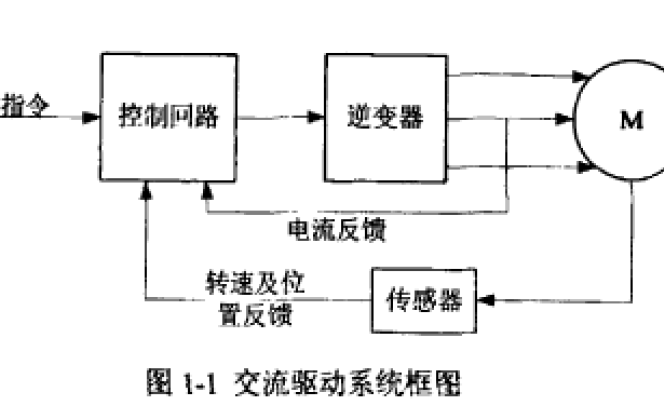
永磁同步電機控制系統的模型建立和仿真資料說明



















評論