今日正文
(1)占空比為50%的方波的傅里葉級數展開
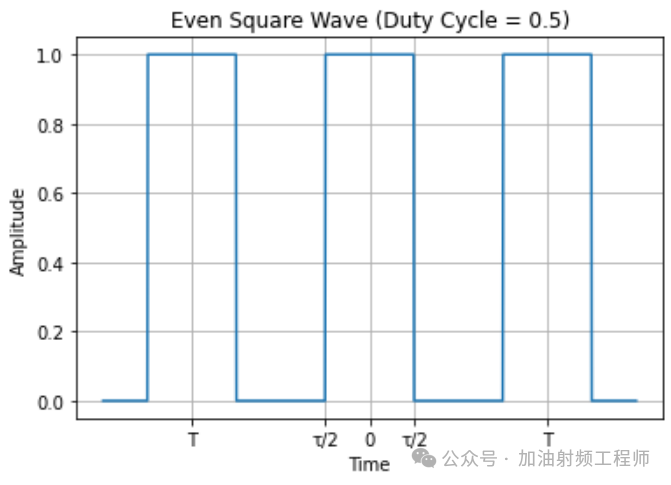
假設有一個方波,周期是T,占空比τ為0.5,幅度為1,如下圖所示。
周期信號的傅里葉級數為:
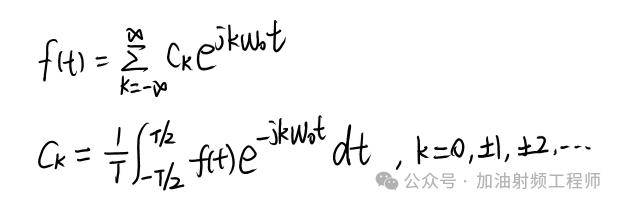
因此,可以求得,方波的各個頻率分量所對應的傅里葉系數Ck,分別為:
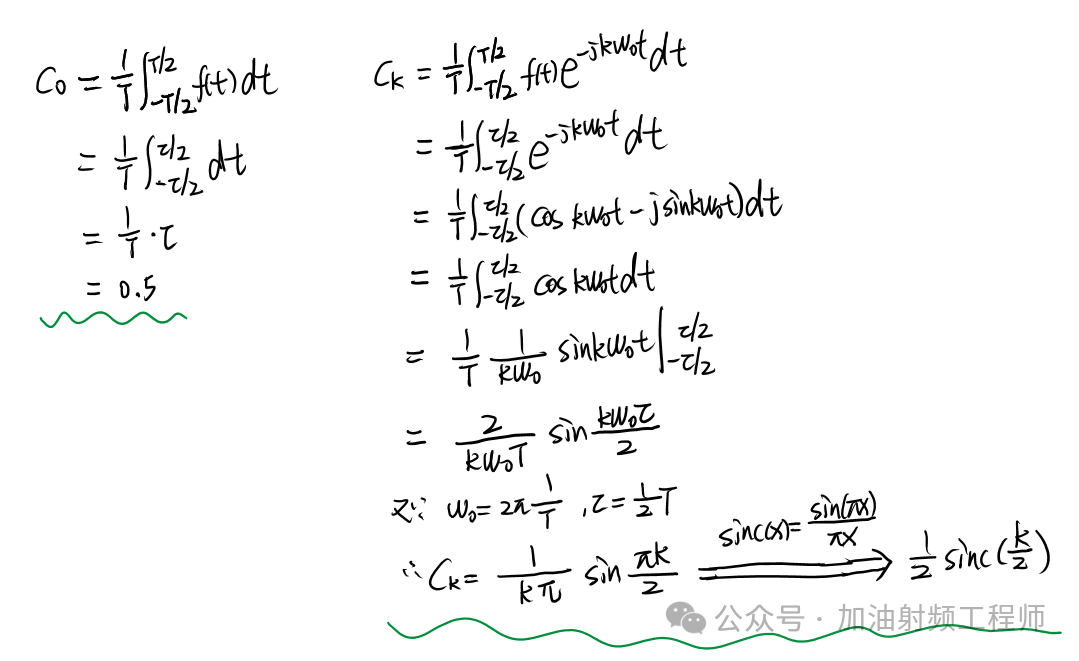
也就是說,方波用傅里葉級數暫開后,可以得到:

也就是說,上述圖示的方波是由直流和一系列不同幅度的余弦函數構成的。
(2)演示一下,用各個分量,慢慢疊加,形成方波。
當只有直流時,圖形為:
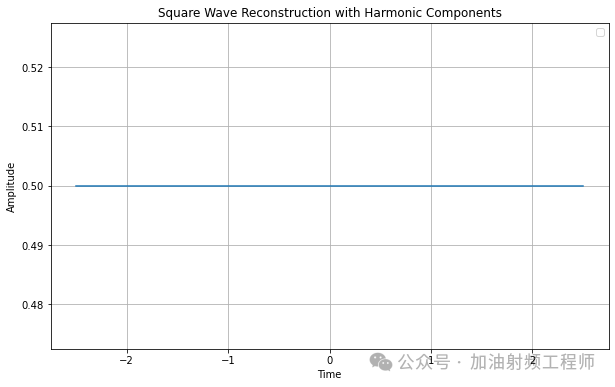
疊加上頻率為w0的余弦信號,圖形為:
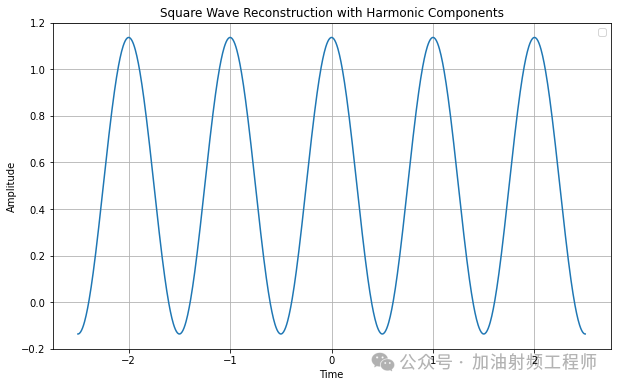
疊加上頻率為3w0的余弦信號,圖形為:
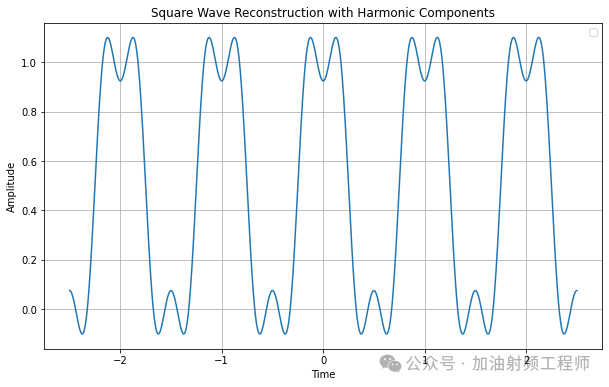
疊加上頻率為5w0的余弦信號,圖形為:
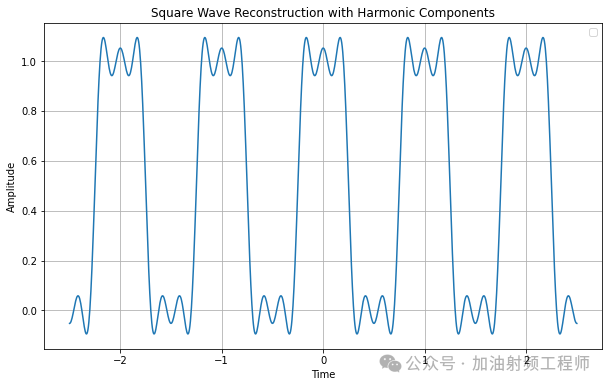
......
疊加上頻率為101w0的余弦信號,圖形為:
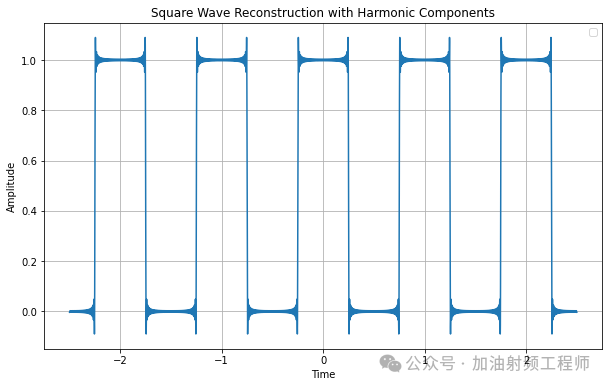
......
疊加上頻率為1001w0的余弦信號后,圖形為:
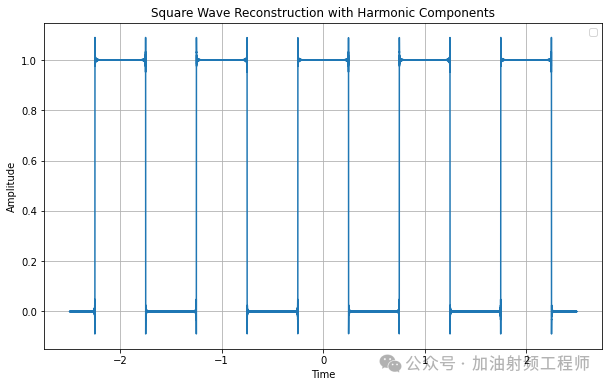
(3)吉布斯現象(Gibbs phenomenon)
由上面的疊加圖形可以看到,當用余弦波疊加去逼近方波信號時,所用的諧波次數N即使增加到1001后,在不連續點的附近,仍然會出現過沖。
N越大,過沖的最大值越接近不連續點,但其峰值并不下降,而是大約等于原函數在不連續點處跳變值的9%。
(4) 上面的圖形的Python程序
import numpy as np import matplotlib.pyplot as plt def square_wave(T, tau, num_periods): """Generate a square wave.""" t = np.linspace(-T * num_periods / 2, T * num_periods / 2, 100000) duty_cycle = tau / T waveform = np.zeros_like(t) waveform[((t+0.25*T) % T) < (duty_cycle * T )] = 1 waveform1=np.ones_like(t)*0.5 return t, waveform,waveform1 def harmonic_component(T, n, amplitude,num_periods): """Generate a harmonic component.""" t = np.linspace(-T * num_periods / 2, T * num_periods / 2, 100000) frequency = n / T component = amplitude * np.cos(2* np.pi * frequency*t) return t, component def main(): """Main function.""" T = 1 # Period tau = 0.5 * T # Pulse width num_periods = 5 # Number of periods to plot num_harmonics = 1001 # Number of harmonics to include # Generate the fundamental square wave t, waveform,waveform1 = square_wave(T, tau, num_periods) # Plot the fundamental square wave plt.figure(figsize=(10, 6)) # plt.plot(t, waveform, label='Fundamental') # Generate and add harmonic components for n in range(1, num_harmonics + 1): _, component = harmonic_component(T, n, np.sinc(n/2),num_periods) waveform1 += component plt.plot(t, waveform1) plt.xlabel('Time') plt.ylabel('Amplitude') plt.title('Square Wave Reconstruction with Harmonic Components') plt.legend() plt.grid(True) plt.show() if __name__ == "__main__": main()
-
python
+關注
關注
56文章
4800瀏覽量
84829 -
余弦函數
+關注
關注
0文章
2瀏覽量
5420 -
傅里葉級數
+關注
關注
1文章
11瀏覽量
2459
原文標題:方波的Gibbs現象
文章出處:【微信號:加油射頻工程師,微信公眾號:加油射頻工程師】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于ATM理念的UTRAN傳輸架構簡析
消除數字濾波器中Gibbs現象的研究
EPON技術簡析
簡析BGA封裝技術與質量控制
簡析比較器的原理及應用資料下載





 方波的Gibbs現象簡析
方波的Gibbs現象簡析










評論