在我們的電子設(shè)計中有一項逃不掉的干擾,那就是電子噪聲。這些電子噪聲通常包括:散彈噪聲(Shot noise),熱噪聲(Thermal Noise),閃變噪聲(Flicker Noise),突發(fā)噪聲(Burst Noise)和雪崩噪聲(Avalanche Noise)等。
電子噪聲的來源多種多樣,對電子設(shè)備的功能和性能產(chǎn)生了重大的影響。如何抑制和減少這些電子噪聲的影響,在如今的電子設(shè)計中尤為重要。
這些噪聲當中,有一項怎么也躲不過去的噪聲,這種噪聲幾乎以一個常數(shù)來影響這接收機的靈敏度,也構(gòu)成了接收機無法逾越的噪底極限—— -174dBm/Hz,它就是熱噪聲。
我們今天一起來認識一下它。
今天的我們都非常熟悉熱噪聲的來源——它是由導體中電子的布朗運動產(chǎn)生的電子噪聲,它是溫度變化的結(jié)果,存在于所有電子器件和傳輸介質(zhì)中,既不能被減小,更不能被忽略,而且在所有頻譜中都以相同的形態(tài)分布,構(gòu)成了所有無線通信系統(tǒng)的上限。
根據(jù)其分布特點,熱噪聲也稱為白噪聲;同時為了紀念它的發(fā)現(xiàn)者——J.B.Johnson 和 Harry Nyquist,也稱為約翰遜噪聲或者奈奎斯特噪聲,或者合稱為約翰遜—奈奎斯特噪聲。
熱噪聲的發(fā)現(xiàn)
奈奎斯特作為通信界大神級別的存在,相信每一個同學都不陌生,其最著名的奈奎斯特采樣定律,構(gòu)成了模擬信號數(shù)字化的理論基礎(chǔ)。但其實熱噪聲真正的發(fā)現(xiàn)者是約翰遜。
1926年,約翰遜在貝爾實驗室中首次發(fā)現(xiàn)并且第一次測量到熱噪聲,他把這個消息告訴了他的好朋友奈奎斯特,并且奈奎斯特也能夠解釋這種現(xiàn)象,于是就有了—— 約翰遜 —奈奎斯特噪聲。
可能有些同學會納悶,這次是不是又被奈奎斯特搶了功勞?畢竟前有香農(nóng)-奈奎斯特采樣定律,這次又有約翰遜-奈奎斯特噪聲。但是我想還是多慮了,這兩位大神的關(guān)系可能非同尋常,都來自瑞典,然后移民美國,并且都在北達科他州大學完成的本科學習,并且都在耶魯大學學習和做研究,之后輾轉(zhuǎn)又都成了貝爾實驗室的同事。在1928年又同時發(fā)表在物理雜志上的兩篇論文又奠定了熱噪聲的基礎(chǔ)。
|
Johnson, John B. “Thermal Agitation of Electricity in Conductors.”The Physical Review32, no. 1 (1928): 97-109. Nyquist, Harry. “Thermal Agitation of Electric Charge in Conductors.”The Physical Review32, no. 1 (1928): 110-113. |
熱噪聲的計算
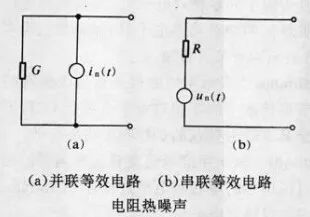
在通信中,電阻熱噪聲有兩種表示方法,一種是采用并聯(lián)等效電路,另一種是采用串聯(lián)等效電路,如下圖所示。并聯(lián)等效電路是由一個無噪聲電導G和一個功率 譜密度為2kTG的噪聲電流源in(t)并聯(lián),串聯(lián)等效電路則由一個無噪聲電阻R和一個噪聲電壓源un(t)串聯(lián)。兩者間可用戴維南等效電源定理轉(zhuǎn)換。
熱噪聲的單邊功率譜密度可以由下面公式計算
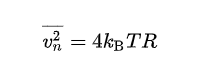
其中,KB是玻爾茲曼常數(shù),等于1.38*10^(-23)J/K ;
T是電阻的絕對溫度,單位為K 開爾文;
R是電阻值,單位為Ω 歐姆;
轉(zhuǎn)換成功率就是
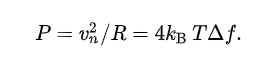
上式就是單位赫茲下的噪聲功率譜密度P。
電阻器所產(chǎn)生的噪聲可以傳遞至其余電路;最大的噪聲功率傳遞發(fā)生在噪聲產(chǎn)生阻抗與剩余電路的戴維南等效阻抗阻抗匹配時。在這種情況下兩部分阻抗中的任意一個的耗散噪聲均作用在其本身和其他電阻。由于其中的任何一個電阻只有一半的壓降,因此噪聲功率為:
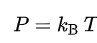
考慮到信號都有一定的帶寬,因此噪聲的功率譜公式又可以寫作:
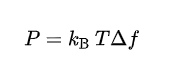
注意,上式中頻率的單位為Hz。
我們射頻人比較喜歡用dB來表示比較小或者大的數(shù)字,當然噪聲功率也不例外。
把上面公式轉(zhuǎn)換成dBm形式就是:
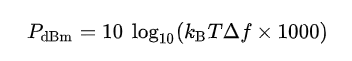
注意上面的1000是dBm中的m是毫瓦,毫瓦和瓦的換算系數(shù)是1000.
進一步化簡,上式可以表示為:
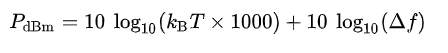
如果只考慮室溫情況下的噪聲功率的話,室溫下T0=294.15K,
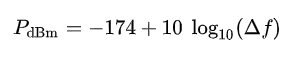
準確的說,第一項的值為-173.9155206 dBm, 約為-174dBm,這也就是-174dBm/Hz的由來了。
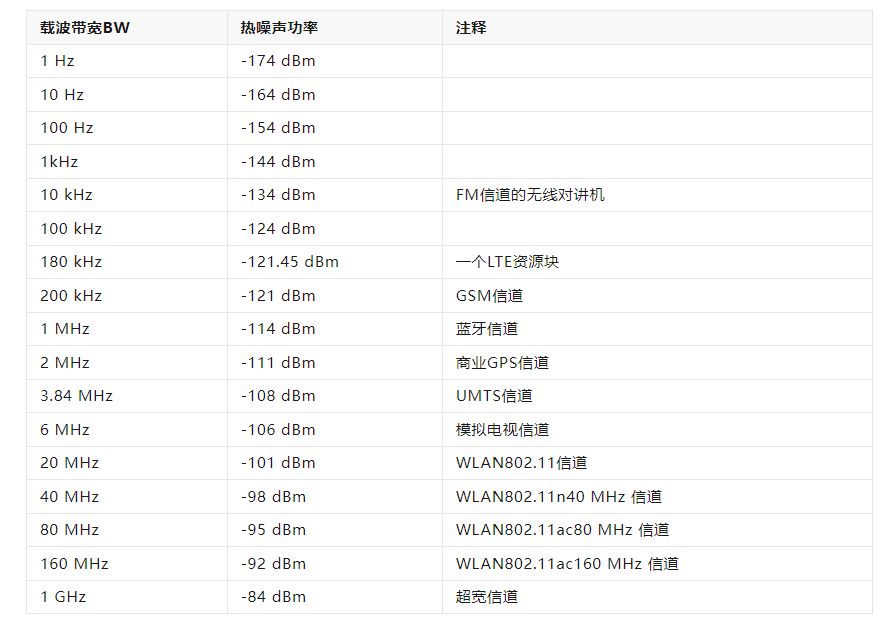
如果信號帶寬為1Hz的話,那么-174dBm,就是噪底了。如果信號帶寬越寬的話,這個噪底被抬升的越高。
如下表所示:
審核編輯:黃飛
-
電阻
+關(guān)注
關(guān)注
86文章
5575瀏覽量
173229 -
接收機
+關(guān)注
關(guān)注
8文章
1189瀏覽量
53797 -
電子設(shè)計
+關(guān)注
關(guān)注
40文章
807瀏覽量
48778 -
熱噪聲
+關(guān)注
關(guān)注
0文章
46瀏覽量
8227 -
等效阻抗
+關(guān)注
關(guān)注
0文章
7瀏覽量
3260
原文標題:什么是熱噪聲? 為什么底噪是-174dBm/Hz?
文章出處:【微信號:射頻學堂,微信公眾號:射頻學堂】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
電磁干擾噪聲抑制片應用介紹pdf
電磁噪聲的抑制方法
HDMI接口的噪聲抑制方法
如何抑制電子電路中噪聲的產(chǎn)生?
如何抑制開關(guān)電源的紋波噪聲
用EMIFIL抑制噪聲應用指南
驅(qū)動電子設(shè)備減少噪聲的設(shè)計
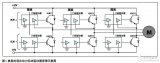
電力電子設(shè)備傳導噪聲抑制措施
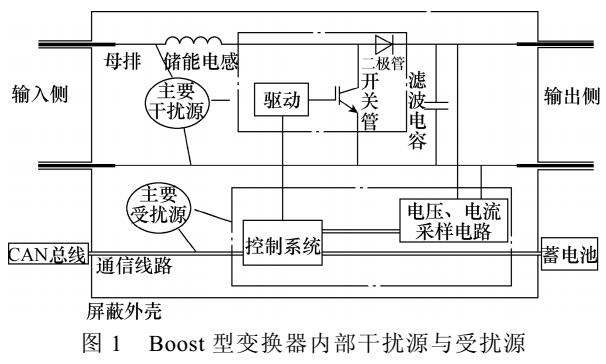
如何才能抑制電源的噪聲
噪聲抑制片的屏蔽性能測試





 如何抑制和減少電子噪聲影響?
如何抑制和減少電子噪聲影響?










評論