原文作者:張天蓉
經典計算機無法模擬量子力學,那就建造一個按照量子力學規律運行的計算機來直接模擬和計算量子世界。
你肯定見過上面這張著名的照片,在29人中有17位諾獎得主,包括愛因斯坦、玻爾、居里夫人等,被稱為是科學史上最牛的合照,照片中的大多數人物對量子力學做出了重要貢獻。
靈魂人物費曼
那是在1981年,歷經了80年風雨的量子理論已經是一門成熟又成功的物理理論。盡管玻爾和愛因斯坦世紀之爭的余波猶存,量子學者們仍舊在孜孜不倦地探究更好的理論詮釋,但是,1964年貝爾不等式的提出,以及之后多次實驗驗證貝爾不等式不成立的事實,已經足以證實量子論的正確,疊加態的存在,量子糾纏的存在。量子物理的實際應用更是無處不在,它曾經直接奠定了原子彈、核技術、光學、半導體等的理論基礎,讓人類贏得了戰爭,給社會帶來了偉大的技術革命。特別是以量子力學為基礎的半導體物理及其應用,促成了晶體管和集成電路兩項偉大的發明,使計算機技術在1970年代急速發展,如日中天。
那年的五月,美國波士頓MIT的校園里,鮮花盛開,綠草如茵。歷史悠久的恩迪科特大廈,正在進行為期三天的熱烈討論。大約 50 位科學家聚集在一起,召開了物理學中的“量子”,和計算機技術的第一次“聯姻”會議,從此揭開了研究發展量子計算機的新篇章[1]。
量子和計算,兩者聽起來似乎風馬牛不相及,為何要“聯姻”呢?
當然,其實兩者本來就有關,如前所述,沒有量子力學作為理論基礎,不可能有半導體工業,也就沒有晶體管,沒有集成電路,沒有如此發達的計算機產業。不過,這一次科學家們所提及的,是實質上的聯姻,是要讓計算機按照量子力學不同尋常的奇妙規律和方式來工作,來進行計算!
這次會議并不是由費曼召集或主持的,但費曼(在照片中標號為38)無疑地成為了那幾天討論的主角,會議的靈魂人物。這是由費曼無限的個人魅力形成的。費曼何許人也!他既是家喻戶曉的偉大科學家,又是極棒的演員和超群的教師。是他眉飛色舞的演講,將物理和計算機專家們的眼光匯聚到一起;是他精彩的辯論,讓與會人士深入理解了大會的主題:計算科學還有瑕疵,但也許能“吸取量子現象的運作方式”而從中受益。
費曼1918年生于紐約一個猶太人家庭。不同于一般理論物理學家在人們心目中的嚴謹刻板形象,費曼被人譽為“一個智慧超凡的科學鬼才”,其傳奇故事膾炙人口。他從小就是個科學頑童,后來不僅是著名的物理學家,也是一位開保險箱專家和經常演出的邦戈鼓手。此外,他還曾經像一位真正的畫家一樣賣掉過自己的好幾幅繪畫作品。他在MIT讀完大學本科后,到普林斯頓大學讀Ph.D.,師從約翰·惠勒。他參加了著名的曼哈頓計劃,開創量子物理中路徑積分的想法,建立了量子電動力學,被授予1965年的諾貝爾物理學獎。
除了量子之外,數學和計算,一直是費曼的樂趣所在。費曼曾經得過普特南數學競賽第一名,在曼哈頓計劃中,費曼負責了多項繁瑣的計算任務,還曾將年輕人組織成“人肉計算機”,流水線般地完成編程式的計算步驟。
現代電子計算機的計算能力,引起了費曼的注意。他與同行們一起鉆研用計算機模擬物理世界的方法,發現這個計算方法只適用于模擬經典的物理世界,對量子世界并不完全適用。
因此,費曼在會議上提出一個新穎的設問:經典計算機可以被用來模擬量子世界嗎?答案是否定的 。因為在模擬量子現象時,經典計算機的計算量,將隨著系統(粒子數N)的增大而指數增加。費曼認為微觀世界的本質是量子的,N非常大,是傳統計算機在有效時間內解決不了的問題。他緊接著就提出一個獨特的設想:能不能發明出一個更新式的計算機,一個按照量子力學規律運行的計算機,以此直接模擬和計算量子世界?
“量子計算機”的概念,從此出現在人們的視野。
第一張“明星照”
我們再回頭看看這張匯聚如此多的精英在同一張相框內的會議明星照。
這時候,距離第一張照片的1927年,已經過去了整整54年。不用仔細對照名字就能知道,兩張照片中不太可能有重疊的人物。大半個世紀過去了,照片1中的量子力學第一代創始人,大都已經駕鶴西去,少數僅存者也到了耄耋之年:德布羅意將近90歲,狄拉克也在準備過80大壽。他們都不在MIT的照片里!
我們能找到的,對量子理論發展作出過重要貢獻的知名人物,是弗里曼·戴森和約翰·惠勒,分別在照片中標號為1和12。這兩位都可以算作是諾貝爾物理獎的“漏網之魚”!戴森是生活在美國的英國人,著名的數學物理學家,戴森為量子電動力學的建立做出了決定性的貢獻,以他命名的物理術語很多,如:戴森球、戴森樹、戴森變換等。他后來一直是普林斯頓高等研究院的教授,直到2020年96歲高齡去世。惠勒是費曼(#38)的老師,現代物理學中有許多他創造的術語:量子泡沫、黑洞、蟲洞等。1980年,惠勒剛從普林斯頓到奧斯丁大學,正值他提出“延遲選擇雙縫思想實驗” 之時,該實驗巧妙地體現了量子力學與傳統實在觀之間的巨大分歧,他后來有一句名言:“萬物皆比特”!
照片中居然有一位大名鼎鼎的早期德國機械計算機發明家:康拉德·楚澤(#15)。但他生不逢時,在創造力最旺盛的年紀,碰到了第二次世界大戰。他制造出了Z-1、Z-2、Z-3、Z-4等一系列計算機,他1941年研制的Z-3,使用二進制和繼電器,是世界上第一個有圖靈完全功能的,可編程的通用圖靈機。戰爭時代的科學家難免悲劇命運,楚澤辛苦的研究和設計工作,被埋沒于戰火硝煙中。楚澤生于1910年,時年71歲,估計是照片中最年長者。
此外還有諸多量子界的、計算機領域的專家和后起之秀:列昂尼德·萊文(43)、諾曼·帕卡德(4)、 阿瑟·伯克斯(35)、大衛·萊因韋伯(14)、 卡爾·亞當·佩特里(17)、愛德華·弗雷德金(9)、湯姆·托弗里(10)、羅爾夫·蘭道爾(11)、保羅·貝尼奧夫(30)、丹尼·希利斯(34) ……還有查爾斯·貝內特,是拍照片的人,所以不在框內。
如今又是43年過去了,一代又一代的精英不斷涌現,眾多分支的物理學家、計算機科學家,都在量子計算的發展中,留下了他們的身影!雖然尚未迎來量子計算的春天,但黑暗漸消曙光微現。況且,科學之精神重在過程,科學家群星們的努力探索,值得記載和傳承。
因為:前人之經驗,后人可為鑒。
費曼提出的問題
那么,費曼到底提出了什么問題呢?
也許你會感到奇怪,計算機的能力已經如此強大,為什么還要研發量子計算機呢?是科學家們別出心裁多此一舉吧?其實是因為經典計算技術中,有一個難以解決的“復雜度”問題。
我們經常說到保密通訊的密碼,什么樣的密碼才是最安全的?當然應該是計算機破譯不了的,或者是說得更準確一些:是計算機在有效的時間內破譯不了的。所謂有效的時間,也就是足夠短的時間。你想想,在戰爭中,總不能花上幾年的時間來破解一條敵軍傳遞的信息吧。不要說幾年,幾天也太慢了啊。這就是說,這類問題的時間“復雜度”太大了。
“復雜度”表征的是所需計算量與問題涉及系統變量數N之間的關系。復雜度分時間和空間,時間復雜度指的是所需計算時間T與系統變量數N之間的關系;空間復雜度指所需比特數B與N之間的關系。兩者實際上互相關聯,我們以時間復雜度為例。
一般來說,計算時間將隨著系統增大而增加。但T的增大因問題而異,T與N可以成線性關系,也可能成平方關系,也有可能是隨著N指數增長。可以用函數 O(1)、O(N)等等來表示復雜度,即表示T隨N增加的快慢。
時間復雜度包括:線性關系O(N)、平方關系O(N2)、立方關系O(N3)等等,最困難的是指數關系:例如O(2N)[2],見圖4。
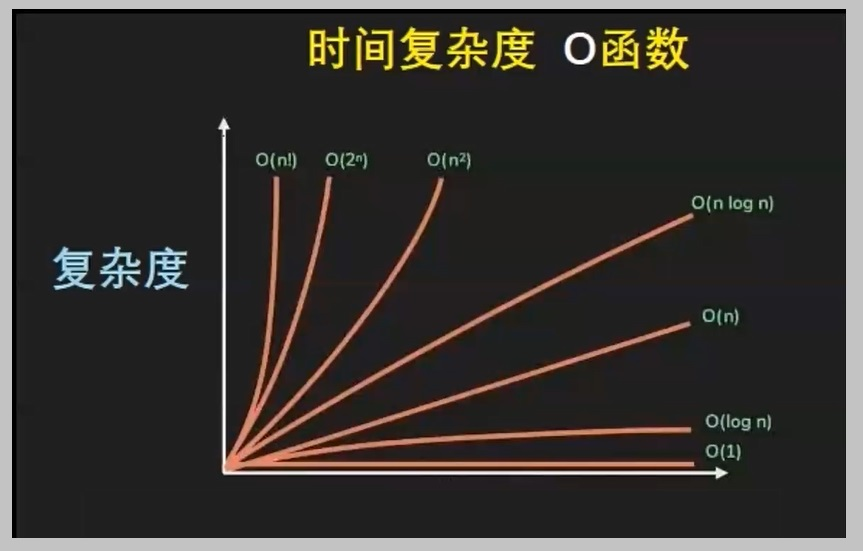
圖4不同問題的不同復雜度
需要注意的是,復雜度指的是,計算時間隨著參數大小變化的規律,并不是具體計算的實際時間。所以復雜度對應于計算機的“計算方式”,即計算機的類型,而非“速度快慢”。舉例來說吧,要破解某條指數關系密碼,1944年的機器計算時間是30年,1980年的機器只需10年,2020年需9年,但它們都是經典計算機,復雜度是一樣的,有限的方式提高速度,改變不了復雜度。
這也就是費曼說的,經典計算機無法模擬量子力學的原因。那么,既然經典的計算機不行,是否有其他的計算模式可以模擬量子世界呢?費曼的想法別出一格,卻又合情合理:他認為微觀世界的本質是量子的,想要模擬它,就得用和自然界的工作原理一樣的方式,也就是量子的方式才行。對此,費曼風趣地表示,既然這個該死的大自然不是經典的,你最好是“模擬它的方法來模擬它”,以其人之道,還治其人之身嘛!我們得做到和大自然做的一模一樣。那就是說,我們要想模擬這個量子行為的世界,就得研究微觀世界的量子是如何工作的,然后,建造一個按照量子力學的規律來運行的計算機,最后才能模擬它。不過,費曼最后又感嘆地說:“天哪,這是一個非常精彩的問題,但卻不是那么容易解決的!”
量子比特vs經典比特
量子計算的方法與經典計算是完全不同的,兩類計算機速度差異的原因是來自于量子現象和經典現象物理規律的不同。量子計算基于量子規律。量子規律的精髓是什么?其實可以用一句話來概括:種種奇怪的量子現象都是來自于量子“疊加態”[3]。
你也許聽過最奇怪的量子現象是“糾纏態”和雙縫實驗,不過實際上,糾纏態也是一種疊加態,是多粒子體系狀態疊加產生的效應,而各類“詭異”的雙縫實驗均可用疊加態解釋。
什么是疊加態呢?根據我們的日常經驗,一個物體在某一時刻總會處于某個固定的狀態。狀態可以用位置、速度、相位、能量等物理參數表示。比如我說,我現在在客廳里,或者說,我現在在房間里。要么在客廳要么在房間,這兩種位置狀態必居其一。然而,在微觀的量子世界中,情況卻有所不同!微觀粒子可以處于一種不確定的狀態中。例如電子可以同時位于兩個(甚至多個)不同的地點。也就是說,電子既在A又在B,電子的狀態是“A”和“B”兩種狀態按一定概率的疊加,物理學家們把電子的這種混合狀態叫做疊加態。
經典世界中的“波”可以是疊加態,但經典“粒子”(宏觀物體)不存在疊加態。比如說,我此時此刻不可能既在客廳又在房間;一只貓要么是死貓要么是活貓,不存在“既死又活”的貓!
微觀量子世界的粒子一般都處于“疊加態”,但是我們卻觀測不到疊加態!原因是因為“觀察測量”的宏觀行為將引起所謂“波函數塌縮”或者被詮釋為“退相干效應”,即觀測之前是疊加態,觀測之后疊加態不復存在,“坍縮” 成了一個確定的狀態!因此,我們只能“以某種概率“觀測到疊加的多個本征態之一。例如,如果盒子中的”薛定諤貓“化身微觀粒子,它的狀態可以被表示成“死貓”與“活貓”的疊加態(如圖5)。
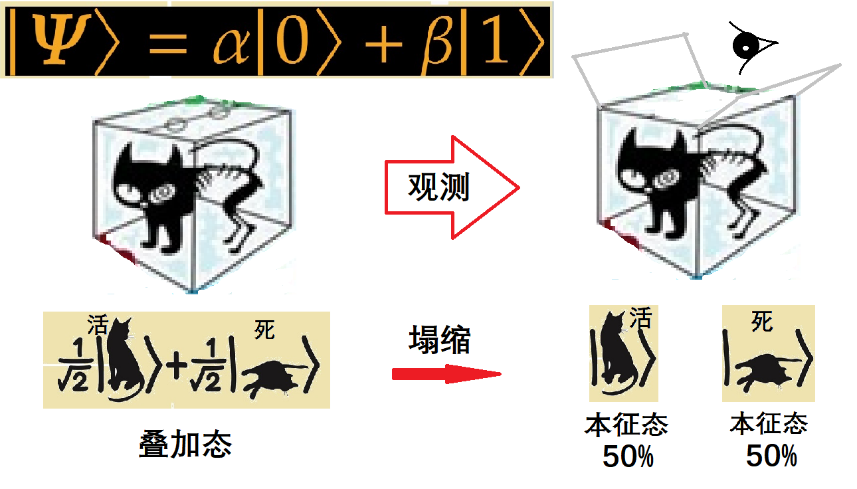
圖5疊加態和坍縮
然而,只要你打開盒子觀測,疊加態就塌縮了!你有50%的可能性看到“活貓”,50%的可能性看到“死貓”,但你看不到“既死又活”的貓,換言之,你觀測不到它們的疊加態!
有時稍微加點數學抽象,更能理解疊加態。因為事實上經典的宏觀物體(比如貓)是沒有疊加態的,完全不用數學便只想到宏觀的直觀經驗,總是試圖用經典概念來理解“疊加態”,這種經典現象又是不可能的。因此可以說,不放棄經典,永遠不可能真懂疊加態!所以,我們最好記住圖5左上角那個疊加態波函數的公式,也就是:|y>= a|0>+ b|1>。
疊加態通常用2分量量子系統來表示,上面公式中的|0>和|1>是系統的兩個本征態。
費曼正是因為對量子理論,對疊加態的深入理解,才能提出量子計算技術的設想。
審核編輯:黃飛
-
計算機
+關注
關注
19文章
7520瀏覽量
88221 -
量子計算
+關注
關注
4文章
1105瀏覽量
34971 -
量子糾纏
+關注
關注
0文章
35瀏覽量
10194
原文標題:費曼:經典計算機可以模擬量子世界嗎?
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 量子世界能否被經典計算機所模擬?
量子世界能否被經典計算機所模擬?











評論