大家好,這就為您獻(xiàn)上不知鴿了多久的Flash Attention V2原理解讀。
在V1的講解中,我們通過詳細(xì)的圖解和公式推導(dǎo),一起學(xué)習(xí)了Flash Attention的整體運(yùn)作流程。如果大家理解了V1的這塊內(nèi)容,就會(huì)發(fā)現(xiàn)V2的原理其實(shí)非常簡單:無非是將V1計(jì)算邏輯中的內(nèi)外循環(huán)相互交換,以此減少在shared memory上的讀寫次數(shù),實(shí)現(xiàn)進(jìn)一步提速。那當(dāng)你交換了循環(huán)位置之后,在cuda層面就可以配套做一些并行計(jì)算優(yōu)化。這就是V2的整體內(nèi)容。
總結(jié)起來一句話:“交換了循環(huán)位置“,雖是短短一句話,卻蘊(yùn)含著深深的人生哲理:只要基座選得好,回回都有迭代點(diǎn),年年勇破okr!
回歸正題,本文也分兩個(gè)部分進(jìn)行講解:原理與cuda層面的并行計(jì)算。
在閱讀本文前,需要先閱讀V1的講解,本文會(huì)沿用V1的表達(dá)符號(hào)及推演思路。
一、Flash Attention V2整體運(yùn)作流程
1.1 V1的運(yùn)作流程
我們先快速回顧一下V1的運(yùn)作流程:以K,V為外循環(huán),Q為內(nèi)循環(huán)。
,遍歷:
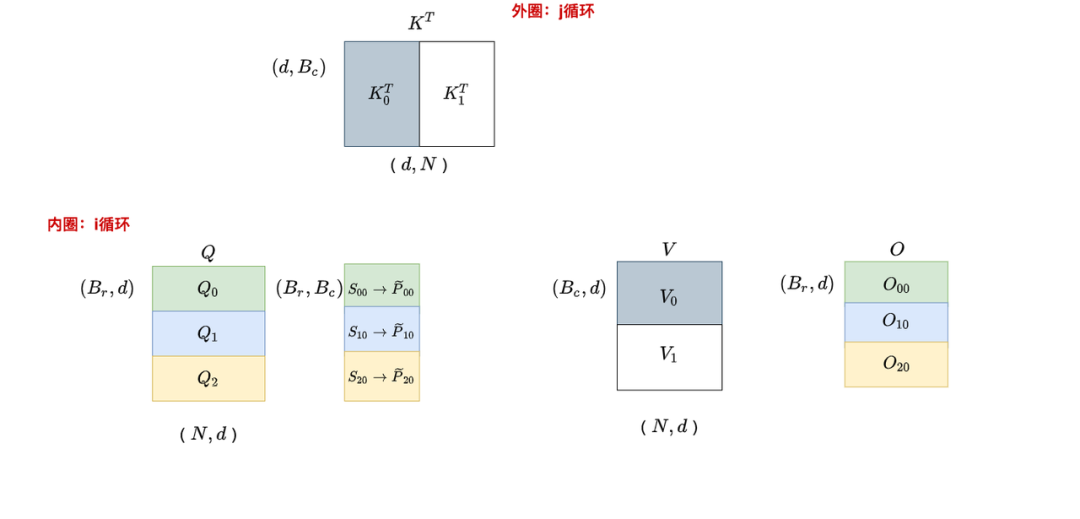
,遍歷:
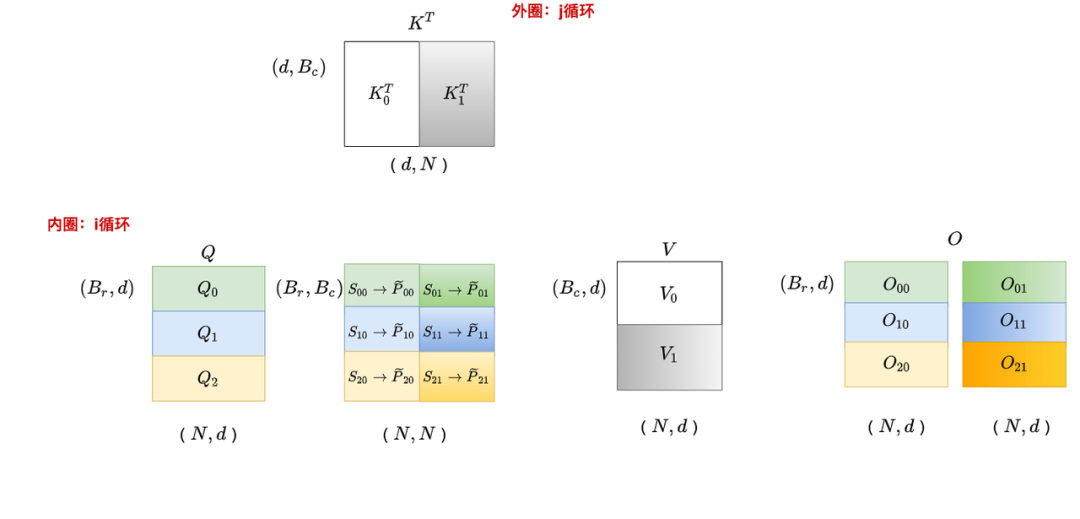
為了幫助大家更好理解v1中數(shù)據(jù)塊的流轉(zhuǎn)過程,在圖中我們畫了6塊O。但實(shí)際上最終只有三塊O:。
以為例,它可理解成是由經(jīng)過某些處理后匯總而來的。進(jìn)一步說,
我們?cè)谕庋h(huán)j = 0時(shí),先遍歷一次所有的i,在這個(gè)階段中我們產(chǎn)出,并將它和一些別的重要數(shù)據(jù)寫回HBM中
接下來我們進(jìn)行第二次外循環(huán),即j=1,在這個(gè)階段中我們產(chǎn)出。同時(shí)我們把和那些重要的數(shù)據(jù)從HBM傳入shared memory中,然后從shared memory中讀取它們,以配合產(chǎn)出最終的
(關(guān)于如何得到的細(xì)節(jié)我們?cè)赩1講解中詳細(xì)推導(dǎo)過,這里不再贅述)
在這個(gè)過程中,你是不是隱隱覺得有些別扭:
其實(shí)都和有關(guān)系,那我為什么不以Q為外循環(huán),以KV為內(nèi)循環(huán)做遍歷呢?這樣我不就能避免往shared memory上讀寫中間結(jié)果,從而一次性把乃至最終的給算出來?
同時(shí),softmax這個(gè)操作也是在row維度上的,所以我固定Q循環(huán)KV的方式,更天然符合softmax的特性。
1.2 V2的運(yùn)作流程
基于1.1中的思想,我們?cè)赩2中將原本的內(nèi)外循環(huán)置換了位置(示意圖就不畫了,基本可以對(duì)比V1示意圖想象出來)。我們直接來看V2的偽代碼(如果對(duì)以下偽代碼符號(hào)表示或解讀有疑惑的朋友,最好先看一下V1的講解)。
(1)V2 FWD

現(xiàn)在,想象自己固定住了一塊Q(i),依此循環(huán)K和V的分塊(j),在這個(gè)想象下我們來解讀這份FWD為代碼。
第8行,計(jì)算分塊
第9行:
表示截止到當(dāng)前分塊(包含當(dāng)前分塊)為止的rowmax
表示使用當(dāng)前每行最大值計(jì)算歸一化前的(我們?cè)赩1中說過,不帶波浪號(hào)的P表示(s-rowmax)/rowsum的結(jié)果,帶波浪號(hào)表示(s-rowmax))
表示截止到當(dāng)前分塊(包含當(dāng)前分塊為止)的rowsum
第10行:表示截止到當(dāng)前分塊(包含當(dāng)前分塊)為止計(jì)算出的O值。由第9和第10行知,當(dāng)我們固定Q循環(huán)KV時(shí),我們每個(gè)分塊都是用當(dāng)前最新的rowmax和rowsum計(jì)算的,同理對(duì)應(yīng)的也是用當(dāng)前最新的rowmax和rowsum計(jì)算的。這樣當(dāng)我們遍歷完所有的KV時(shí),得到的就等于最終全局的結(jié)果。相關(guān)的證明我們?cè)赩1講解中給過,這里不再贅述,只額外提兩點(diǎn):
可能在有些朋友下載的V2論文中,第十行這里O前面的因子項(xiàng)是,這個(gè)公式應(yīng)該是錯(cuò)誤的(大家動(dòng)手推一下就可知,初次看到時(shí)讓我困擾了很久)。在作者個(gè)人主頁的論文鏈接中,這個(gè)typo已經(jīng)被修正。
你可能已發(fā)現(xiàn)這個(gè)O的計(jì)算中缺少歸一化的一項(xiàng),這一項(xiàng)其實(shí)放到了第12行做統(tǒng)一計(jì)算。這也是V2優(yōu)化的一個(gè)點(diǎn):盡量減少非矩陣的計(jì)算,因?yàn)樵?a href="http://m.1cnz.cn/tags/gpu/" target="_blank">GPU中,非矩陣計(jì)算比矩陣計(jì)算慢16倍。
比起V1,V2中不用再存每一Q分塊對(duì)應(yīng)的和了。但是在BWD的過程中,我們?nèi)孕枰?/strong>來做和的重計(jì)算,這樣才能用鏈?zhǔn)角髮?dǎo)法則把dQ,dK,dV正常算出來。V2在這里用了一個(gè)很巧妙的方法,它只存一個(gè)東西(代碼13行,這樣又能進(jìn)一步減少shared memory的讀寫):,這個(gè)等式中小寫的m和l可以理解成是全局的rowmax和rowsum。在接下來BWD的講解中,我們會(huì)來看到這一項(xiàng)的妙用。
(2)V2 BWD
一個(gè)建議:如果你在閱讀本節(jié)中覺得很困惑,一定記得先去看V1的BWD部分,有非常詳細(xì)的推導(dǎo)介紹。看完再來看本節(jié)就很順暢了。

我們觀察到,在V2 BWD中,內(nèi)外循環(huán)的位置又換回來了,即還是KV外循環(huán),Q內(nèi)循環(huán),這是為什么呢?
我們知道在BWD的過程中,我們主要是求(為了求它們還需要求中間結(jié)果,我們來總結(jié)一下這些梯度都需要沿著哪些方向AllReduce:
:沿著i方向做AllReduce,也就是需要每行的結(jié)果加總
:沿著i方向做AllReduce,也就是需要每行的結(jié)果加總
:沿著j方向做AllReduce,也就是需要每列的結(jié)果加總
:只與當(dāng)前i,j相關(guān)
基于此,如果你還是保持Q外循環(huán),KV外循環(huán)不變的話,這種操作其實(shí)是固定行,遍歷列的,那么在這些梯度中,只有從中受益了,K和V的梯度則進(jìn)入了別扭的循環(huán)(也意味著要往shared memory上寫更多的中間結(jié)果);但如果你采用KV外循環(huán),Q內(nèi)循環(huán),這樣K和V都受益,只有Q獨(dú)自別扭,因此是一種更好的選擇。(S和P的計(jì)算不受循環(huán)變動(dòng)影響)。
前面說過,在BWD過程中讀寫我們要用全局的重新計(jì)算,計(jì)算公式如下:
但如此一來,我們就要從shared memory上同時(shí)讀取,似乎有點(diǎn)消耗讀寫。所以在V2中,我們只存儲(chǔ),然后計(jì)算:
很容易發(fā)現(xiàn)這兩個(gè)計(jì)算是等價(jià)的,但V2的做法節(jié)省了讀寫量
好,現(xiàn)在我們就把V2相對(duì)于V1在計(jì)算原理上的改進(jìn)介紹完了。接下來我們總結(jié)一下V2相對(duì)于V1所有的改進(jìn)點(diǎn)。
二、V2相對(duì)V1的改進(jìn)點(diǎn)
之所以把這塊內(nèi)容放到“V2整體流程介紹”之后,是想讓大家在先理解V2是怎么做的基礎(chǔ)上,更好體會(huì)V2的優(yōu)點(diǎn)。
總體來說,V2從以下三個(gè)方面做了改進(jìn):
置換內(nèi)外循環(huán)位置,同時(shí)減少非矩陣的計(jì)算量。(這兩點(diǎn)我們?cè)诘谝徊糠种幸呀o出詳細(xì)說明)
優(yōu)化Attention部分thread blocks的并行化計(jì)算,新增seq_len維度的并行,使SM的利用率盡量打滿。這其實(shí)也是內(nèi)外循環(huán)置換這個(gè)總體思想配套的改進(jìn)措施
優(yōu)化thread blocks內(nèi)部warp級(jí)別的工作模式,盡量減少warp間的通訊和讀取shared memory的次數(shù)。
第二和第三點(diǎn)都可以歸結(jié)為是cuda gemm層面的優(yōu)化,我們馬上來細(xì)看這兩點(diǎn)。
三、V2中的thread blocks排布
//gridDiminV1 //params.b=batch_size,params.h=num_heads dim3grid(params.b,params.h); //gridDiminV2 constintnum_m_block=(params.seqlen_q+Kernel_traits::kBlockM-1)/Kernel_traits::kBlockM; dim3grid(num_m_block,params.b,params.h);
這段代碼整合自flash attention github下的cutlass實(shí)現(xiàn),為了方便講解做了一點(diǎn)改寫。
這段代碼告訴我們:
在V1中,我們是按batch_size和num_heads來劃分block的,也就是說一共有batch_size * num_heads個(gè)block,每個(gè)block負(fù)責(zé)計(jì)算O矩陣的一部分
在V2中,我們是按batch_size,num_heads和num_m_block來劃分block的,其中num_m_block可理解成是沿著Q矩陣行方向做的切分。例如Q矩陣行方向長度為seqlen_q(其實(shí)就是我們熟悉的輸入序列長度seq_len,也就是圖例中的N),我們將其劃分成num_m_block份,每份長度為kBlockM(也就是每份維護(hù)kBlockM個(gè)token)。這樣就一共有batch_size * num_heads * num_m_block個(gè)block,每個(gè)block負(fù)責(zé)計(jì)算矩陣O的一部分。
為什么相比于V1,V2在劃分thread block時(shí),要新增Q的seq_len維度上的劃分呢?
先說結(jié)論,這樣做的目的是盡量讓SM打滿。我們知道block是會(huì)被發(fā)去SM上執(zhí)行的。以1塊A100 GPU為例,它有108個(gè)SM,如果此時(shí)我們的block數(shù)量比較大(例如論文中所說>=80時(shí)),我們就認(rèn)為GPU的計(jì)算資源得到了很好的利用。現(xiàn)在回到我們的輸入數(shù)據(jù)上來,當(dāng)batch_size和num_heads都比較大時(shí),block也比較多,此時(shí)SM利用率比較高。但是如果我們的數(shù)據(jù)seq_len比較長,此時(shí)往往對(duì)應(yīng)著較小的batch_size和num_heads,這是就會(huì)有SM在空轉(zhuǎn)了。而為了解決這個(gè)問題,我們就可以引入在Q的seq_len上的劃分。
看到這里你可能還是有點(diǎn)懵,沒關(guān)系,我們通過圖解的方式,來一起看看V1和V2上的thread block到底長什么樣。
3.1 V1 thread block
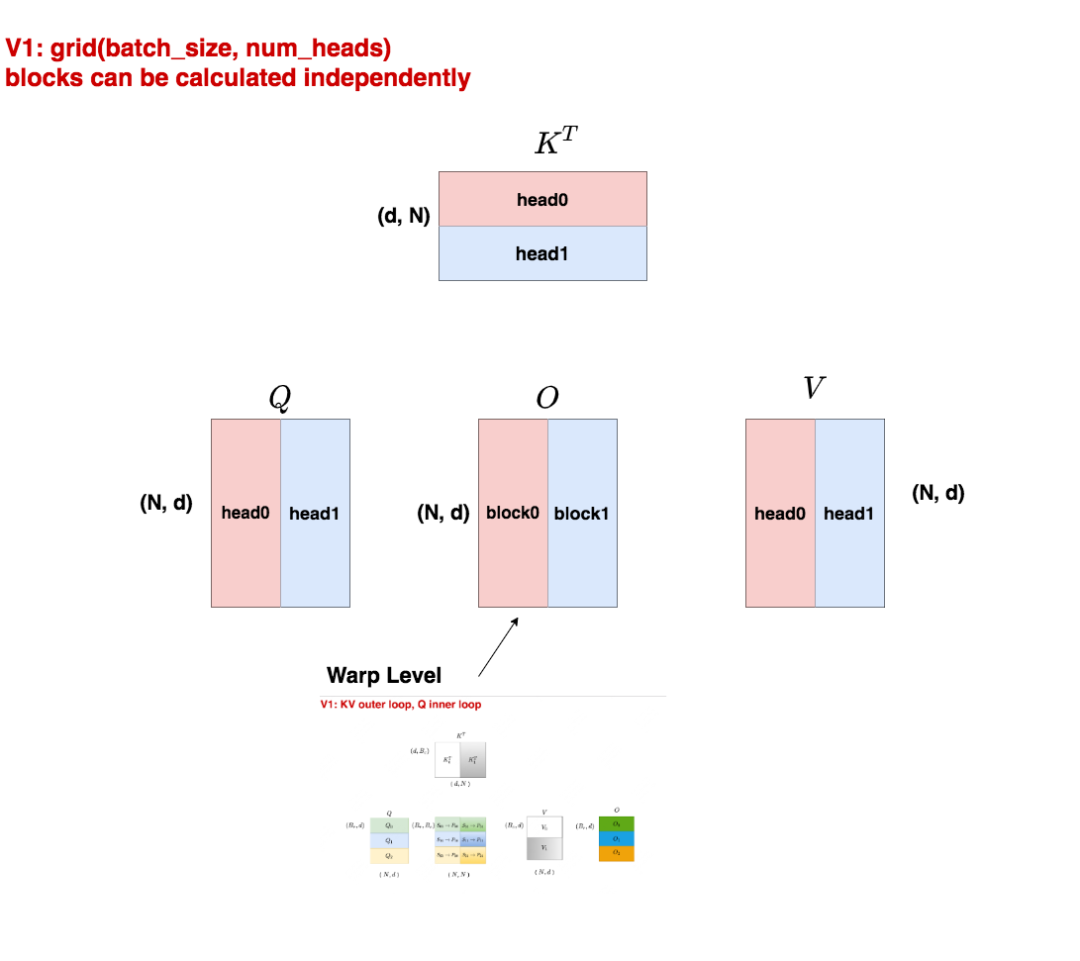
假設(shè)batch_size = 1,num_heads = 2,我們用不同的顏色來表示不同的head。
我們知道在Multihead Attention中,各個(gè)head是可以獨(dú)立進(jìn)行計(jì)算的,在計(jì)算完畢后將結(jié)果拼接起來即可。所以我們將1個(gè)head劃分給1個(gè)block,這樣就能實(shí)現(xiàn)block間的并行計(jì)算,如此每個(gè)block只要在計(jì)算完畢后把結(jié)果寫入自己所維護(hù)的O的對(duì)應(yīng)位置即可。
而每個(gè)block內(nèi),就能執(zhí)行V1中的"KV外循環(huán),Q內(nèi)循環(huán)”的過程了,這個(gè)過程是由block的再下級(jí)warp level層面進(jìn)行組織,thread實(shí)行計(jì)算的。這塊我們放在第四部分中講解。
3.2 V2 thread block
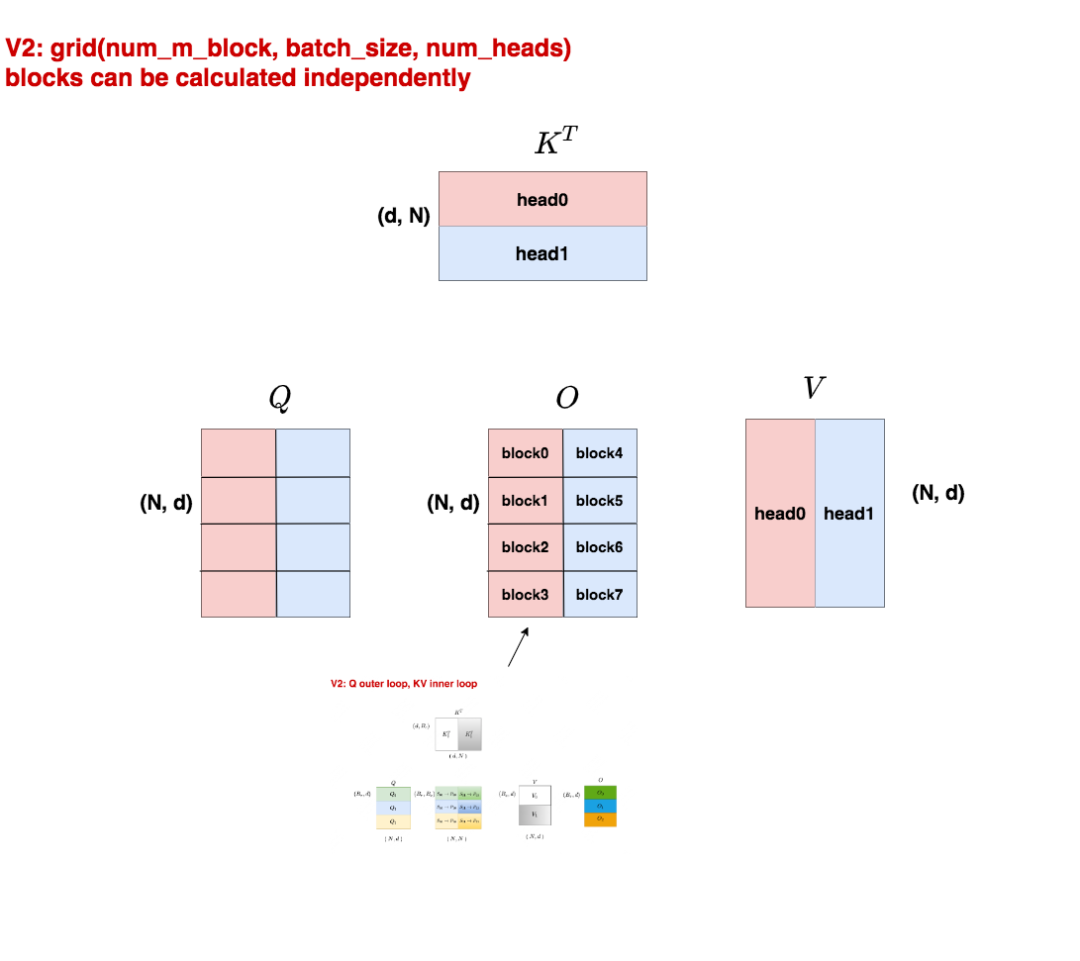
現(xiàn)在我們繼續(xù)假設(shè)batch_size = 1,num_heads = 2。
與V1不同的是,我們?cè)赒的seq_len維度上也做了切分,將其分成四份,即num_m_block = 4。所以現(xiàn)在我們共有124 = 8個(gè)block在跑。這些block之間的運(yùn)算也是獨(dú)立的,因?yàn)椋?/p>
head的計(jì)算是獨(dú)立的,所以紅色block和藍(lán)色block互不干擾
采用Q做外循環(huán),KV做內(nèi)循環(huán)時(shí),行與行之間的block是獨(dú)立的,因此不同行的block互相不干擾。
每個(gè)block從Q上加載對(duì)應(yīng)位置的切塊,同時(shí)從KV上加載head0的切塊,計(jì)算出自己所維護(hù)的那部分O,然后寫入O的對(duì)應(yīng)位置。
在這里你可能想問,為什么只對(duì)Q的seq_len做了切分,而不對(duì)KV的seq_len做切分呢?
在V2的cutlass實(shí)現(xiàn)中,確實(shí)也提供了對(duì)KV的seq_len做切分的方法。但除非你認(rèn)為SM真得打不滿,否則盡量不要在KV維度上做切分,因?yàn)槿绱艘粊恚煌腷lock之間是沒法獨(dú)立計(jì)算的(比如對(duì)于O的某一行,它的各個(gè)部分來自不同的block,為了得到全局的softmax結(jié)果,這些block的結(jié)果還需要匯總做一次計(jì)算)。
3.3 seq parallel不是V2特有
如果你看過V1的代碼,你會(huì)發(fā)現(xiàn),其實(shí)在V1后期的版本中,也出現(xiàn)了seq維度的并行:
//V1seqparallel:csrc/flash_attn/src/fmha_fwd_launch_template.h dim3grid(launch_params.params.b,launch_params.params.h,launch_params.params.num_splits); //nums_splits計(jì)算方法 //Findthenumberofsplitsthatmaximizestheoccupancy.Forexample,ifwehave //batch*n_heads=48andwehave108SMs,having2splits(efficiency=0.89)is //betterthanhaving3splits(efficiency=0.67).However,wealsodon'twanttoomany //splitsasthatwouldincurmoreHBMreads/writes. //Sowefindthebestefficiency,thenfindthesmallestnumberofsplitsthatgets95% //ofthebestefficiency. //[2022-11-25]TD:Markthisas"inline"otherwiseweget"multipledefinition"error. inlineintnum_splits_heuristic_fwd(intbatch_nheads,intnum_SMs,intctas_per_sm,intmax_splits){ floatmax_efficiency=0.f; std::vectorefficiency; efficiency.reserve(max_splits); for(intnum_splits=1;num_splits<=?max_splits;?num_splits++)?{ ????????float?n_waves?=?float(batch_nheads?*?num_splits)?/?(num_SMs?*?ctas_per_sm); ????????float?eff?=?n_waves?/?ceil(n_waves); ????????//?printf("num_splits?=?%d,?eff?=?%f ",?num_splits,?eff); ????????if?(eff?>max_efficiency){max_efficiency=eff;} efficiency.push_back(eff); } for(intnum_splits=1;num_splits<=?max_splits;?num_splits++)?{ ????????if?(efficiency[num_splits?-?1]?>0.95*max_efficiency){ //printf("num_splitschosen=%d ",num_splits); returnnum_splits; } } return1; } .... //可以發(fā)現(xiàn)num_splits也是由Q的seq_len維度切分來的 launch_params.params.num_splits=num_splits_heuristic_fwd( launch_params.params.b*launch_params.params.h,dprops->multiProcessorCount, ctas_per_sm, /*max_splits=*/std::min(30,(launch_params.params.seqlen_q+M-1/M)) );
上圖代碼中的num_splits也是在由Q的seq_len維度切分來的。通過這段代碼,我猜想作者在V1后期引入seq_len維度切分的原因是:V1也需要解決seq_len過長時(shí),batch_size和num_heads較小而造成SM打不滿的問題。
num_splits_heuristic_fwd這個(gè)函數(shù)的作用概括起來就是,我先提供一連串num_splits值的備選,然后由這個(gè)函數(shù)計(jì)算出每個(gè)備選值下SM的利用率。計(jì)算完之后,我先找到最高的利用率,然后再找出滿足利用率>=0.95 * max(利用率)的那個(gè)最小的num_split值,作為最終的選擇。
細(xì)心的你此時(shí)可能已經(jīng)觀察到了,雖然V1也引進(jìn)過seq parallel,但是它的grid組織形式時(shí)(batch_size, num_heads, num_m_blocks),但V2的組織形式是(num_m_blocks, batch_size, num_heads),這種順序調(diào)換的意義是什么呢?
直接說結(jié)論,這樣的調(diào)換是為了提升L2 cache hit rate。大家可以看下3.2中的圖(雖然block實(shí)際執(zhí)行時(shí)不一定按照?qǐng)D中的序號(hào)),對(duì)于同一列的block,它們讀的是KV的相同部分,因此同一列block在讀取數(shù)據(jù)時(shí),有很大概率可以直接從L2 cache上讀到自己要的數(shù)據(jù)(別的block之前取過的)。
3.4 FWD和BWD過程中的thread block劃分
在3.1~3.3中,我們其實(shí)給出的是FWD過程中thread block的劃分方式,我們知道V2中FWD和BWD的內(nèi)外循環(huán)不一致,所以對(duì)應(yīng)來說,thread block的劃分也會(huì)有所不同,我們?cè)敿?xì)來看:

在圖中:
worker表示thread block,不同的thread block用不同顏色表示
整個(gè)大方框表示輸出矩陣O
我們先看左圖,它表示FWD下thread block的結(jié)構(gòu)。每一行都有一個(gè)worker,它表示O矩陣的每一行都是由一個(gè)thread block計(jì)算出來的(假設(shè)num_heads = 1),這就對(duì)應(yīng)到我們3.1~3.3中說的劃分方式。那么白色的部分表示什么呢?我們知道如果采用的是casual attention,那么有一部分是會(huì)被mask掉的,所以這里用白色來表示。但這不意味著thread block不需要加載白色部分?jǐn)?shù)據(jù)對(duì)應(yīng)的KV塊,只是說在計(jì)算的過程中它們會(huì)因被mask掉而免于計(jì)算(論文中的casual mask一節(jié)有提過)。
我們?cè)倏从覉D,它表示BWD下thread block的結(jié)構(gòu),每一列對(duì)應(yīng)一個(gè)worker,這是因?yàn)锽WD中我們是KV做外循環(huán),Q做內(nèi)循環(huán),這種情況下dK, dV都是按行累加的,而dQ是按列累加的,少數(shù)服從多數(shù),因此這里thread_block是按的列劃分的。
四、Warp級(jí)別并行
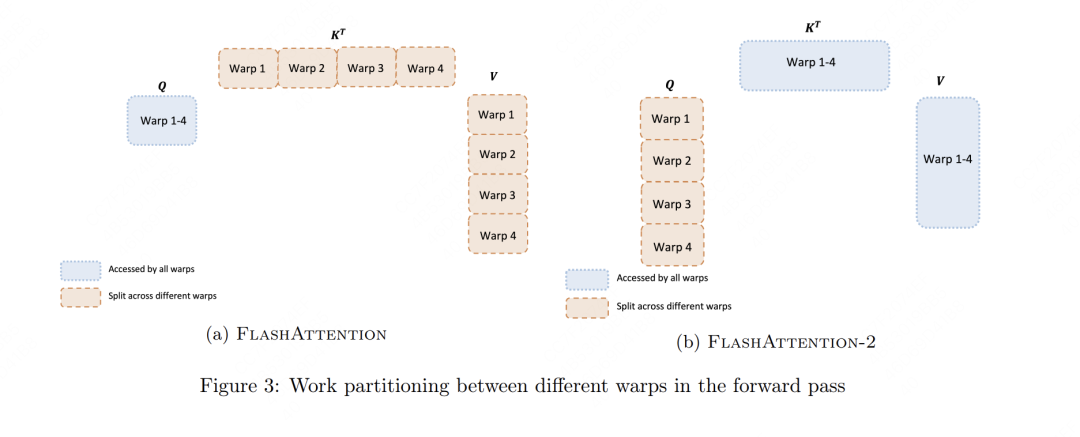
講完了thread block,我們就可以再下一級(jí),看到warp level級(jí)別的并行了。左圖表示V1,右圖表示V2。不管是V1還是V2,在Ampere架構(gòu)下,每個(gè)block內(nèi)進(jìn)一步被劃分為4個(gè)warp,在Hopper架構(gòu)下則是8個(gè)warp。
在左圖(V1)中,每個(gè)warp都從shared memory上讀取相同的Q塊以及自己所負(fù)責(zé)計(jì)算的KV塊。在V1中,每個(gè)warp只是計(jì)算出了列方向上的結(jié)果,這些列方向上的結(jié)果必須匯總起來,才能得到最終O矩陣行方向上的對(duì)應(yīng)結(jié)果。所以每個(gè)warp需要把自己算出來的中間結(jié)果寫到shared memory上,再由一個(gè)warp(例如warp1)進(jìn)行統(tǒng)一的整合。所以各個(gè)warp間需要通訊、需要寫中間結(jié)果,這就影響了計(jì)算效率。
在左圖(V2)中,每個(gè)warp都從shared memory上讀取相同的KV塊以及自己所負(fù)責(zé)計(jì)算的Q塊。在V2中,行方向上的計(jì)算是完全獨(dú)立的,即每個(gè)warp把自己計(jì)算出的結(jié)果寫到O的對(duì)應(yīng)位置即可,warp間不需要再做通訊,通過這種方式提升了計(jì)算效率。不過這種warp并行方式在V2的BWD過程中就有缺陷了:由于bwd中dK和dV是在行方向上的AllReduce,所以這種切分方式會(huì)導(dǎo)致warp間需要通訊。
針對(duì)V2 warp切分影響B(tài)WD這點(diǎn),作者在論文中依然給出了“BWD過程相比V1也有提升”的結(jié)論,針對(duì)這點(diǎn),我在github issue上找到了一條作者的回復(fù)(在“安裝報(bào)錯(cuò)”組成的issue海洋里撈出的寶貴一條):
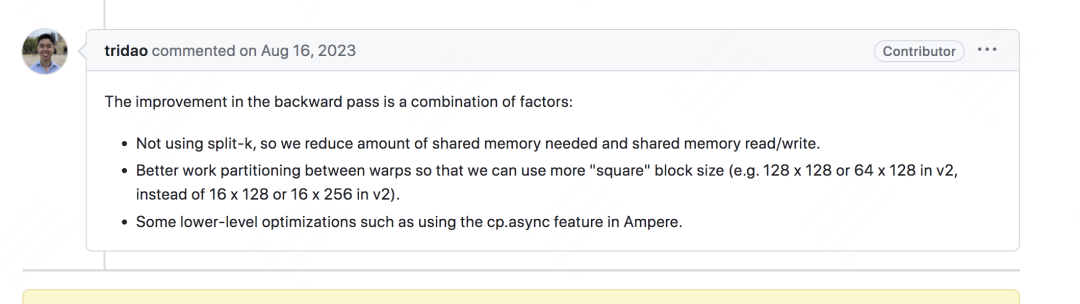
最關(guān)鍵的可能是第1和第2點(diǎn),關(guān)于第1點(diǎn),我想作者應(yīng)該是說,之前需要反復(fù)讀取KV的數(shù)據(jù),現(xiàn)在只用反復(fù)讀取Q的數(shù)據(jù),因此從一定程度上節(jié)省了shared memory的讀寫次數(shù)。第2點(diǎn)理解起來有點(diǎn)復(fù)雜,個(gè)人覺得是將warp處理的tile劃分得更像方形。這樣做的好處是在做casual mask的時(shí)候可以方便寫代碼大塊丟掉被mask掉的tile(見論文casual masking部分),進(jìn)一步加速計(jì)算。第3點(diǎn)是關(guān)于一些底層的優(yōu)化,就不提了。
好!關(guān)于V2我們就介紹到這了,寫這篇文章的時(shí)候,我剛粗過了一遍triton的flash attention實(shí)現(xiàn),以及掃了一下cutlass實(shí)現(xiàn)的入口。如果后續(xù)有時(shí)間,我會(huì)出一些源碼解讀的文章(從cuda gemm -> triton gemm -> triton flash attention,看,又給自己挖了一個(gè)坑)。如果出不了,那一定不是我鴿人,那肯定是我不會(huì)(沒錯(cuò),就是這樣)。
審核編輯:黃飛
-
gpu
+關(guān)注
關(guān)注
28文章
4861瀏覽量
130201 -
并行計(jì)算
+關(guān)注
關(guān)注
0文章
28瀏覽量
9527 -
大模型
+關(guān)注
關(guān)注
2文章
2873瀏覽量
3607
原文標(biāo)題:圖解大模型計(jì)算加速系列:Flash Attention V2,從原理到并行計(jì)算
文章出處:【微信號(hào):zenRRan,微信公眾號(hào):深度學(xué)習(xí)自然語言處理】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
我可以使用ST-LINK/V2為STM8S系列編程閃存嗎?
ST-LINK/V2 ST-LINK/V2ST-LINK / V2在調(diào)試器/編程器STM8和STM32
Kinect v2(Microsoft Kinect for Windows v2 )配置移動(dòng)電源解決方案

Kinect v2(Microsoft Kinect for Windows v2 )配置移動(dòng)電源解決方案

學(xué)習(xí)V2更新板開源分享

智能BMS V2開源設(shè)計(jì)

NodeMCU V2 Amica V3 Lolin的盾牌




















評(píng)論