脈沖信號用于電子和無線電的各個領域。一個特殊的例子是在雷達信號中,但還存在許多其他應用。
鑒于它們的使用,通常需要使用頻譜分析儀來測量信號的特性。然而,它們被脈沖的事實提出了一些有趣的挑戰。
傳統上,脈沖頻譜分析技術和方法通常針對穩定的模擬射頻信號。然而,脈沖頻譜分析需要對所分析的信號有一點了解,這可以獲得額外的信息。
射頻脈沖信號或任何形式的脈沖信號有多種形式,但盡管種類繁多,但它們具有許多共同特征。這意味著可以應用常見的脈沖頻譜分析技術。
要了解用于脈沖信號頻譜分析的技術,首先需要了解脈沖波形的基本性質。它的重復時間為 T,脈沖持續時間為 t。
使用傅里葉分析可以看出,該波形由基波和諧波組成。方波的基本波形可以由與方波重復率相同的基波正弦波組成,然后是奇次諧波,諧波幅度與其數量成反比。
矩形脈沖只是這一基本原理的延伸。通過改變諧波的相對幅度和相位(奇數和偶數)來獲得不同的波形形狀。
脈沖波形由基波及其諧波組成
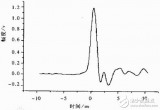
然后可以繪制這些基帶信號,并繪制無限次諧波的幅度和相位,包括奇數和偶數,從而產生如下所示的平滑包絡。
完美矩形脈沖的頻譜
然后可以將該單波調制到射頻波形上以提供頻譜。隨著基帶信號的諧波延伸到無窮大,調制信號的邊帶也延伸到無窮大。然而,在現實中,帶寬永遠不會是無限的,諧波,尤其是高階諧波會衰減。雖然這會導致信號失真,但電平通常是可以接受的。
調制到具有相位反轉的射頻載波上的脈沖波形頻譜
脈沖頻譜分析
已經可以看到脈沖信號是如何產生的,以及由此產生的光譜。雖然邊帶的相位在上圖中得到了調整,但頻譜分析儀是標量測試儀器,通常不會指示信號的相位。因此,頻譜分析儀的繪圖僅顯示“在線上方”。
調制到射頻載波上的脈沖波
形的標量頻譜,即僅包括幅度。
為此,可以注意以下幾點:
光譜線:調制波形圖上顯示的各個頻譜線之間相隔的頻率等于 1/T。
信封中的空值:光譜包絡或整體形狀中的零點以 1/t 的間隔出現。在n / t處出現進一步的零點
包絡零清晰度:由于調制信號的上升和下降時間有限,并且存在由此產生的不對稱性,因此脈沖頻譜形狀中的零點并不總是特別明顯。
脈沖脫敏
有時,脈沖脫敏問題在脈沖頻譜分析中會提到。問題在于,當調制施加到載波時,包絡的峰值電平會降低,似乎信號的總功率已經降低。
峰值幅度明顯降低是因為將脈沖添加到信號中并用方波調制會導致功率在載波和邊帶之間分配。隨著調制電平的增加,邊帶電平也會增加。由于可用的功率有限,并且每個頻譜分量(即載波和邊帶)僅包含總功率的一小部分。
在頻譜分析儀上看到的總體效果是峰值功率降低,但它分布在更寬的帶寬上。
可以α定義脈沖脫敏因子。這可以用等式來描述:
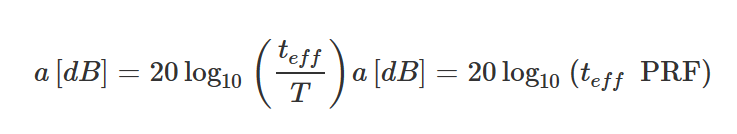
應該注意的是,這種關系只對真正的傅里葉線譜有效。為此,分析儀的分辨率帶寬應<0.3 PRF。
信號的平均功率還取決于占空比,因為只有當信號處于可以粗略地稱為“ON”狀態時,才能輻射功率。這可以通過以下公式定義:
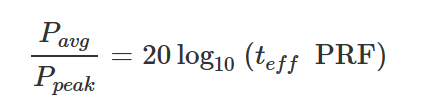
其中:
α = 脈沖“衰退因子
T = 脈沖重復率
PRF = 脈沖重復頻率 (1 / T)
t = 脈沖長度 teff = 有效脈沖長度
,考慮上升和下降時間
Pavg = 脈沖周期
內的平均功率 Ppeak = 峰值功率
三角形和梯形波形
雖然脈沖頻譜分析通常應用于方波或矩形波形,但類似的原理也適用于三角形和梯形波形。
波形的格式與脈沖波形具有許多相似的特征,但具有不同組成信號的電平,因此具有不同的邊帶。
因此,可以以類似的方式分析這些波形。
脈沖頻譜分析測量技巧
當使用頻譜分析儀查看脈沖信號時,有必要采用技術來確保顯示信號以揭示所需的方面。
一些主要方面是:
小于行距的測量帶寬:為了分辨單個譜線,測量帶寬必須相對于譜線的偏移量很小,即帶寬< 1 / T。如果測量帶寬進一步降低,它們譜線將保留其值(如預期的那樣),但噪聲水平將降低,盡管測量時間會更長。
行距和零點間距之間的測量帶寬:當測量帶寬大于光譜線間距但小于零點間距時,將發生下一階段。在這種情況下,譜線無法分辨,包絡的振幅高度取決于帶寬。這是因為更多的光譜線,每條都有自己的功率貢獻,包含在測量帶寬內。對于這種情況,1 / t > B > 1 / T。
大于零點間距的測量帶寬:對于測量帶寬大于信號頻譜包絡上的零點間距(即 B > 1 / T)的情況,無法識別信號的幅度分布。
隨著脈沖傳輸的廣泛應用,脈沖頻譜分析是表征和測試任何開發的設備及其產生的信號的重要元素。
審核編輯:黃飛
-
射頻
+關注
關注
104文章
5588瀏覽量
167779 -
無線電
+關注
關注
60文章
2144瀏覽量
116501 -
頻譜
+關注
關注
7文章
882瀏覽量
45638 -
傅里葉
+關注
關注
0文章
59瀏覽量
20475 -
脈沖信號
+關注
關注
6文章
399瀏覽量
36979
發布評論請先 登錄
相關推薦
頻譜分析儀入門指南:基礎知識詳解
Chirp脈沖波形的性能參數對脈沖頻譜的影響介紹
如何用泰克高端示波器和頻譜分析儀,來分析雷達脈沖信號
脈沖激光器對金屬中激光超聲信號的頻譜分析




 脈沖信號頻譜分析基礎知識:脈沖波形的基本性質
脈沖信號頻譜分析基礎知識:脈沖波形的基本性質
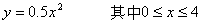











評論