來源:德思特測量測試德思特干貨丨如何使用SBench6軟件對數字化儀采集信號進行處理?(一)——波形算術運算與直方圖功能
歡迎關注虹科,為您提供最新資訊!
1****前言
板卡式數字化儀可以實現準確、高分辨率的數據采集,并能快速傳輸到計算機主機。在計算機主機中應用的信號處理程序,可以幫助用戶獲得更多的數據,或從簡單的測量中提取出極為有用的信息。
現代板卡式數字化儀,會有一系列軟件為其提供功能增強支持。比如德思特SBench 6和許多第三方程序,都包含多種信號處理功能。這些功能包括波形算術運算、分組和滑動平均、快速傅立葉變換(FFT)、高級濾波功能和直方圖。本文將展開介紹上述這些功能,并提供這些處理工具的典型應用示例。
2****模擬量運算(波形算術運算)
模擬量運算包括對獲取到的波形進行加減乘除四則運算。這些應用于波形的運算可以改善信號質量,或推導出其它更多有用的信息。其中一例子是使用減法運算,將差分信號組合成具有更低共模噪聲和拾取水平的差分波形。而另一個例子則是將電流和電壓波形進行乘積,計算瞬時功率曲線。
所有這些算術函數都應用于波形的上的每一個采樣點數據。首先,我們假設要合成的波形具有相同的采樣點長度。我們按照圖1顯示的路徑,在SBench 6軟件中找到“Analog Calculation(模擬運算)”設置項的位置。
圖1:SBench 6中針對每個信號的運算處理選項
右鍵單擊需要參與運算的原始通道,在彈出的選擇框中選擇“Simple Measurements(采樣點測量)”、“Signal Calculations(信號計算)”、“Signal Conversion(信號轉換)”和“Signal Averaging(信號平均)”會展示額外的選項。例如,信號計算選擇提供了模擬運算、快速傅立葉變換(FFT)、直方圖、濾波和其他幾種函數運算。如果選擇了模擬預算,運算對話框會彈出,允許設置所需的算術運算。在圖中例子中,AI-Ch0和AI-Ch1兩個原始信號將被相加。其他選項包括減法(SUB)、乘法(MULTI)和除法(DIV)。其他剛才提到的信號處理函數也可以用類似的方式進行選擇和設置。
接下來,我們會展示將波形算術運算應用于實際問題的第一個示例,那就是將一個信號組件從另一個信號中減去,以計算差分信號,如圖2所示。
圖2:使用減法功能,從兩個差分通道信號中得出差分信號
差分技術通常用于改善信號的完整性。在圖2所示的示例中,1 MHz時鐘的“P”和“N”成分(在兩個右側窗格中顯示)使用減法運算進行合并。得到的差分信號在中間窗格中顯示。而左側中部的“Info”窗格,則使用峰峰值和平均值兩個指標對每個波形進行了測量。我們很容易看出,差分信號的峰峰值接近原來的兩倍,并且平均值接近零。此外,差分成分中的共模噪聲已被消除。
第二個示例是將電壓波形與電流波形相乘,以獲得如圖3所示的瞬時功率。
圖3:使用乘法函數從開關電源的電流及電壓波形計出算瞬時功率
原始波形是功率場效應晶體管(FET)上的電壓和在開關電源的Flyback模式下FET的通過電流。這些波形的乘積表示FET瞬時消耗的功率。電流波形(右上窗格)在FET導通期間線性增加,峰值約為600 mA。FET上的電壓在導通期間則最小,但在關斷時升至260V的峰值。這兩個波形的乘積在左側窗格中顯示,這就是瞬時功率波形。波形體現了在導通和關斷狀態之間的轉換時出現顯著的功率尖峰。而平均值(5.111 W)和峰值功率(44.25 W)則顯示在左側中部的“Info”窗格中。
這些示例展現了使用模擬運算從原始波形中獲取出其他重要的波形的能力和方法。
3****直方圖
我們還可以在統計域中查看數據。這通常用于獲知某些幅度值發生的概率,而實現的方式則是繪制波形幅值與其出現頻次的直方圖。所得的直方圖就是信號概率分布的有限記錄長度估計。在德思特SBench 6軟件中,我們提供了創建已獲取波形直方圖的能力。圖4中顯示了一系列示例,包括正弦波,三角波和噪聲波形以及它們對應的直方圖分布。
圖4:一些常見波形示例,以及它們對應的直方圖
上面一行窗格顯示了正弦波、三角波和噪聲波的原始波形,下面一行則是對應的直方圖。其中,直方圖的水平軸表示信號的幅度。垂直軸顯示在小范圍內(分組)的值的數量。
每個波形的直方圖分布都是獨特的,差異與信號本身的特性有關。正弦波的直方圖分布顯示在兩端上有高峰,而中部呈鞍形。形成這種形狀的原因是正弦波的幅值在整個周期內都在變化,且變化率(導數)在零交點處最高,在峰值處最低。如果將正弦波以均勻的時間間隔切割成小片段,那么在正峰值(直方圖的最右側峰值)和負峰值(直方圖的最左側峰值)處會有更多的樣本片段,在零交點(在直方圖的水平中心)處樣本最少。
三角波則具有恒定的斜率絕對值,只是斜率正負在發生變化。結果就是其直方圖具有均勻的分布,除了在兩側最極端處。峰值存在是因為信號發生器具有有限的帶寬,這會使得峰值波形變圓,從而使得在這一段上獲取的樣本更多。
眾所周知,噪聲信號的直方圖一般呈現高斯或正態分布,其原因不再贅述。高斯分布的特征在于它沒有邊界。其他分布一般有幅度限制,水平范圍是固定的。而高斯分布有很長的“尾部”,理論上是可以向兩側延伸到無窮大的,但在實際儀器操作中,其“尾部”會被數字化儀的采集電平范圍所限制。
因此,直方圖也能一定程度上反映信號的問題。它們尤其適用于顯示波形的不對稱性(失真)和小概率發生瑕疵。圖5展示了一個帶有過零失真的正弦波信號對應的直方圖。
圖5:帶有過零失真的正弦波信號,及其對應的直方圖
審核編輯 黃宇
-
信號
+關注
關注
11文章
2804瀏覽量
77007 -
波形
+關注
關注
3文章
379瀏覽量
31624 -
數字化
+關注
關注
8文章
8846瀏覽量
62050 -
數字化儀
+關注
關注
0文章
144瀏覽量
17986
發布評論請先 登錄
相關推薦

簡儀科技高速PXIe數字化儀產品亮點
TLV990-13完整的CCD信號處理器/數字化儀數據表

TLV990-21完整的CCD信號處理器/數字化儀數據表

TLV990-40完整的CCD和視頻信號處理器/數字化儀數據表

TLV990-28完整的CCD信號處理器/數字化儀數據表

德思特Spectrum控制中心為數字化儀提供強大的軟件支持
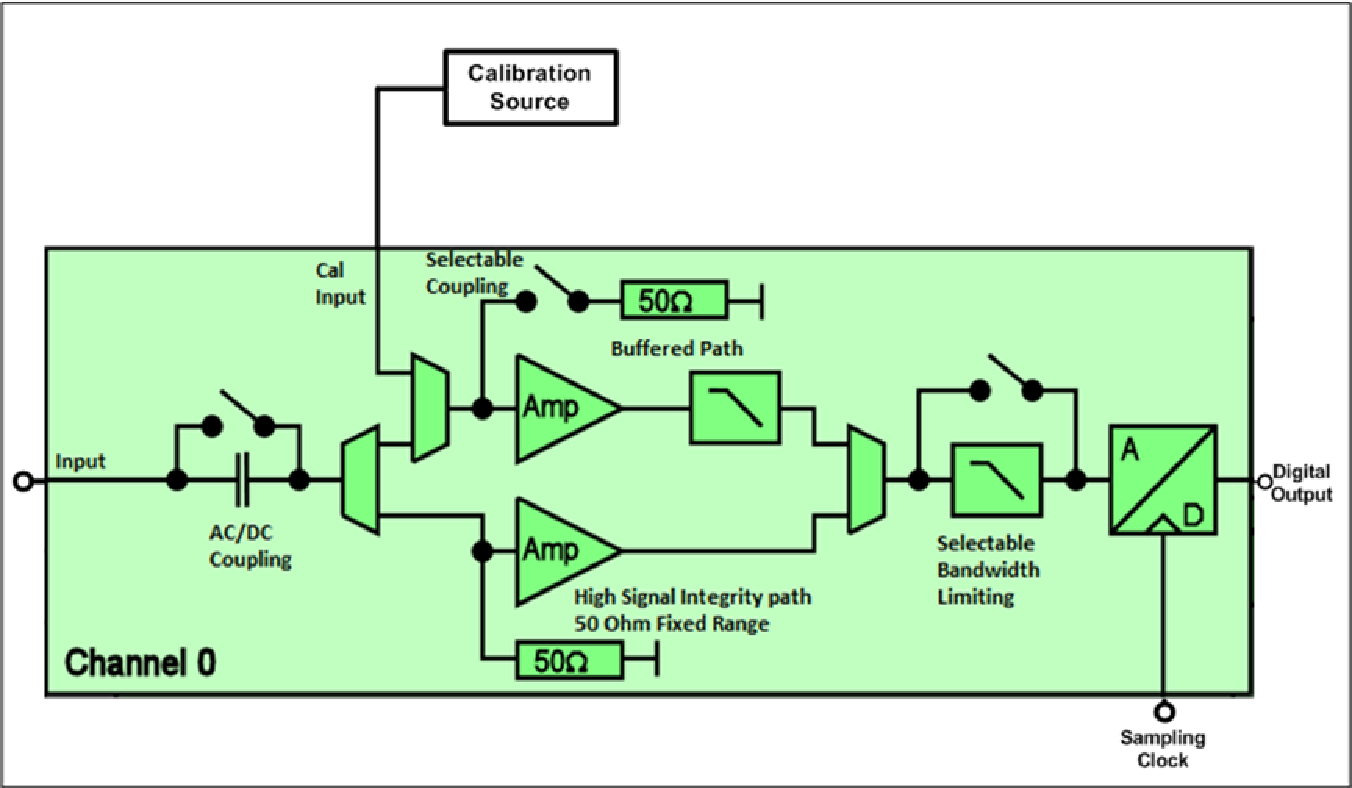
如何正確使用數字化儀前端信號調理?(一)





 如何使用SBench6軟件對數字化儀采集信號進行處理?(一)——波形算術運算與直方圖功能
如何使用SBench6軟件對數字化儀采集信號進行處理?(一)——波形算術運算與直方圖功能











評論