卡爾曼濾波(Kalman Filter)是一種遞歸的、自適應的濾波算法,廣泛應用于估計系統狀態和觀測過程中的噪聲。它最初在1960年被提出,被認為是控制理論和信號處理領域中最重要的發展之一。卡爾曼濾波器在許多領域,包括導航、機器人、金融和通信系統中都有廣泛的應用。
1,基本原理:
卡爾曼濾波器的核心思想是融合系統的動態模型和實際的觀測數據,通過對過程和測量噪聲的估計,提供對系統狀態的最優估計。其基本原理可以分為兩個步驟:預測(Predict)和更新(Update)。
預測(Predict):
在預測階段,卡爾曼濾波器使用系統的動態模型,以及先前的狀態估計來預測系統的下一個狀態。這一過程基于系統的狀態方程和控制輸入,考慮系統的動態演變。預測的結果是對系統狀態的先驗估計,其中考慮了系統的動態行為。卡爾曼濾波的狀態方程通常表示為:
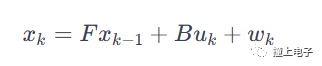
其中,Xk是系統狀態向量,F 是狀態轉移矩陣,B 是輸入矩陣,Uk是控制輸入向量,Wk是過程噪聲。
更新(Update):
在更新階段,卡爾曼濾波器使用實際的測量數據來校正先前的狀態估計。這一過程基于測量方程和測量噪聲,考慮了觀測到的系統輸出。更新的結果是對系統狀態的后驗估計,其中融合了測量信息。
卡爾曼濾波的測量方程通常表示為:
??=???+??
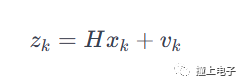
其中,Zk是測量向量,H是測量矩陣,Vk測量噪聲。
2,狀態估計的迭代過程:
卡爾曼濾波是一個迭代的過程,其更新步驟依賴于預測和測量的相互作用。以下是卡爾曼濾波的迭代過程:
初始化: 首先,需要初始化卡爾曼濾波器的狀態估計(X0)和協方差矩陣(P0)
預測: 使用系統的狀態方程進行狀態的預測,并更新狀態的協方差矩陣。這一步考慮了系統的動態演變和過程噪聲。其中,Xk是先驗狀態估計,Pk是先驗協方差矩陣,Q是過程噪聲協方差矩陣。
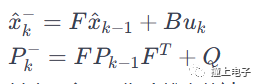
測量更新: 使用測量方程將預測的狀態與實際的測量數據進行比較,從而校正狀態估計,并更新協方差矩陣。這一步考慮了觀測到的系統輸出和測量噪聲。其中,Kk是卡爾曼增益,R是測量噪聲協方差矩陣,Xk是后驗狀態估計,Pk是后驗協方差矩陣。
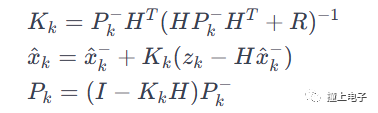
重復: 重復預測和測量更新步驟,將后驗狀態估計作為下一步的先驗狀態估計,持續迭代。
3,關鍵概念:
卡爾曼增益: 卡爾曼增益是一個關鍵的概念,它決定了預測和測量更新之間的相對權重。卡爾曼增益越大,系統對測量數據的依賴性越強,反之亦然。
協方差矩陣: 協方差矩陣描述了狀態估計的不確定性。通過在迭代過程中更新協方差矩陣,卡爾曼濾波器能夠動態調整對狀態估計的信任程度。
過程噪聲和測量噪聲: 過程噪聲和測量噪聲是卡爾曼濾波中的兩個關鍵參數,它們用于描述系統動態模型和測量過程中的不確定性。適當估計和調整這些噪聲是卡爾曼濾波器性能的關鍵。
4,示例代碼:
#include // 定義狀態向量的維度#define STATE_DIM 2// 定義測量向量的維度#defineMEASURE_DIM1
// 定義卡爾曼濾波器結構體typedef struct { // 狀態估計向量 float x[STATE_DIM]; // 狀態協方差矩陣 float P[STATE_DIM][STATE_DIM]; // 過程噪聲協方差矩陣 float Q[STATE_DIM][STATE_DIM]; // 測量噪聲協方差矩陣 float R[MEASURE_DIM][MEASURE_DIM]; // 狀態轉移矩陣 float F[STATE_DIM][STATE_DIM]; // 測量矩陣 float H[MEASURE_DIM][STATE_DIM];} KalmanFilter;
// 初始化卡爾曼濾波器void kalmanFilterInit(KalmanFilter *kf, float initialX, float initialP);// 卡爾曼濾波預測步驟voidkalmanPredict(KalmanFilter*kf,floatcontrolInput);// 卡爾曼濾波更新步驟void kalmanUpdate(KalmanFilter *kf, float measurement);
int main() { // 初始化卡爾曼濾波器 KalmanFilter kf;kalmanFilterInit(&kf,0.0,1.0);
// 模擬輸入數據 float controlInput = 0.1;floatmeasurementNoise=0.5;
// 模擬10次迭代 for (int i = 0; i < 10; ++i) { // 預測步驟 kalmanPredict(&kf, controlInput); // 模擬測量 float trueMeasurement = 2.0 * kf.x[0] + measurementNoise; // 更新步驟????????kalmanUpdate(&kf,?trueMeasurement);
// 打印結果 printf("Iteration %d - True Value: %f, Estimated Value: %f\n", i + 1, trueMeasurement, kf.x[0]); }
return 0;}
// 初始化卡爾曼濾波器void kalmanFilterInit(KalmanFilter *kf, float initialX, float initialP) { // 初始化狀態估計向量 kf->x[0] = initialX; kf->x[1] = 0.0; // 初始化狀態協方差矩陣 kf->P[0][0] = initialP; kf->P[0][1] = 0.0; kf->P[1][0] = 0.0; kf->P[1][1] = initialP; // 初始化過程噪聲協方差矩陣 kf->Q[0][0] = 0.001; kf->Q[0][1] = 0.0; kf->Q[1][0] = 0.0; kf->Q[1][1] = 0.001; // 初始化測量噪聲協方差矩陣kf->R[0][0]=0.01;
// 初始化狀態轉移矩陣 kf->F[0][0] = 1.0; kf->F[0][1] = 1.0; kf->F[1][0] = 0.0; kf->F[1][1] = 1.0; // 初始化測量矩陣 kf->H[0][0] = 1.0; kf->H[0][1] = 0.0;}
// 卡爾曼濾波預測步驟void kalmanPredict(KalmanFilter *kf, float controlInput) { // 預測狀態估計 kf->x[0] = kf->F[0][0] * kf->x[0] + kf->F[0][1] * kf->x[1] + controlInput; // 預測狀態協方差矩陣 kf->P[0][0] = kf->F[0][0] * kf->P[0][0] * kf->F[0][0] + kf->F[0][1] * kf->P[1][0]; kf->P[0][1] = kf->F[0][0] * kf->P[0][1] * kf->F[0][1] + kf->F[0][1] * kf->P[1][1]; kf->P[1][0] = kf->F[1][0] * kf->P[0][0] * kf->F[0][0] + kf->F[1][1] * kf->P[1][0]; kf->P[1][1] = kf->F[1][0] * kf->P[0][1] * kf->F[0][1] + kf->F[1][1] * kf->P[1][1] + kf->Q[1][1];}// 卡爾曼濾波更新步驟void kalmanUpdate(KalmanFilter *kf, float measurement) { // 計算卡爾曼增益 float K[STATE_DIM][MEASURE_DIM];floatS;
// 計算卡爾曼增益 S = kf->H[0][0] * kf->P[0][0] * kf->H[0][0] + kf->R[0][0]; K[0][0] = kf->P[0][0] * kf->H[0][0] / S;K[1][0]=kf->P[1][0]*kf->H[0][0]/S;
// 更新狀態估計 kf->x[0] = kf->x[0] + K[0][0] * (measurement - kf->H[0][0] * kf->x[0]);kf->x[1]=kf->x[1]+K[1][0]*(measurement-kf->H[0][0]*kf->x[0]);
// 更新狀態協方差矩陣 kf->P[0][0] = (1 - K[0][0] * kf->H[0][0]) * kf->P[0][0]; kf->P[0][1] = (1 - K[0][0] * kf->H[0][0]) * kf->P[0][1]; kf->P[1][0] = -K[1][0] * kf->H[0][0] * kf->P[0][0] + kf->P[1][0]; kf->P[1][1] = -K[1][0] * kf->H[0][0] * kf->P[0][1] + kf->P[1][1];}
卡爾曼濾波的優勢在于它能夠提供對系統狀態的最優估計,同時適應于線性和高斯噪聲的系統。然而,卡爾曼濾波也有一些限制,例如對非線性系統的適應性較差,且需要對系統動態模型和噪聲參數進行良好的估計。
-
濾波
+關注
關注
10文章
667瀏覽量
56683 -
信號處理
+關注
關注
48文章
1032瀏覽量
103316 -
C代碼
+關注
關注
1文章
89瀏覽量
14321
發布評論請先 登錄
相關推薦




 卡爾曼濾波的原理和C代碼
卡爾曼濾波的原理和C代碼
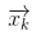
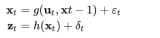










評論