1. 圖像梯度

首先我們來看看什么是圖像梯度：圖像梯度可以把圖像看作二維離散函數，圖像梯度就是這個二維函數的求導，圖像邊緣一般都是通過對圖像進行梯度運算來實現的

在圖像梯度這一部分我們會接觸查找圖像梯度、邊緣等，這一部分涉及了三個主要函數：cv.Sobel()，cv.Scharr()，cv.Laplacian()，相對應的，OpenCV提供的三種類型的梯度濾波器（高通濾波器），即Sobel、Scharr和Laplacian

在上一部分2D卷積即圖像過濾內容中我們說了低通濾波器（LPF）與高通濾波器（HPF）的主要應用方向，LPF用于消除噪聲，HPF用于找到邊緣，在圖像梯度這一部分我們使用三個高通濾波器來找到圖像中的邊緣

1.1 Sobel和Scharr算子

Sobel算子是高斯平滑與微分操作的結合體，所以其抗噪聲能力很好，我們可以設定求導方向（xorder或yorder），還可以設定使用的卷積核大小ksize

當我們設定的卷積核的大小為-1時，會默認使用3x3的Scharr濾波器，它的效果比3x3的Sobel效果更好，并且處理速度相同，所以在使用3x3Sobel濾波器時應使用Scharr濾波器代替

從上面所說的概念我們可以理解為：使用3x3內核的Sobel濾波器并不等于Scharr濾波器，但Scharr濾波器是一種3x3內核的高效濾波器，若我們需要3x3內核的Sobel濾波器，那我們建議使用Scharr濾波器，即在使用Sobel濾波器時設定其內核大小為-1

了解了Sobel和Scharr高通濾波器的內核，我們再來看看cv.Sobel()和cv.Scharr()函數的參數，cv.Sobel(img,cv.CV_64F,dx,dy,ksize)函數需要傳遞的參數分別是原圖像，cv.CV_64F是圖像深度，一般寫作-1就可以了，dx和dy分別表示x軸方向和y軸方向的算子，ksize就是內核

而Scharr高通濾波器是3x3的內核，所以cv.Scharr()的參數與cv.Sobel()函數對比少傳遞一個ksize參數即可

1.2 Laplacian算子

Laplace其實利用Sobel算子的運算，它通過Sobel算子運算出圖像在x方向和y方向的導數，得出拉普拉斯變換結果，它就像Sobel算子的升級版

下面我們上倆例子方便大家理解

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread(r'E:image	est06.png', 0)
laplacian = cv.Laplacian(img, cv.CV_64F)
sobelx = cv.Sobel(img, cv.CV_64F, 1, 0, ksize=5)
sobely = cv.Sobel(img, cv.CV_64F, 0, 1, ksize=5)
plt.subplot(2, 2, 1), plt.imshow(img, cmap='gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 2), plt.imshow(laplacian, cmap='gray')
plt.title('Laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 3), plt.imshow(sobelx, cmap='gray')
plt.title('Sobel X'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 4), plt.imshow(sobely, cmap='gray')
plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])
plt.show()

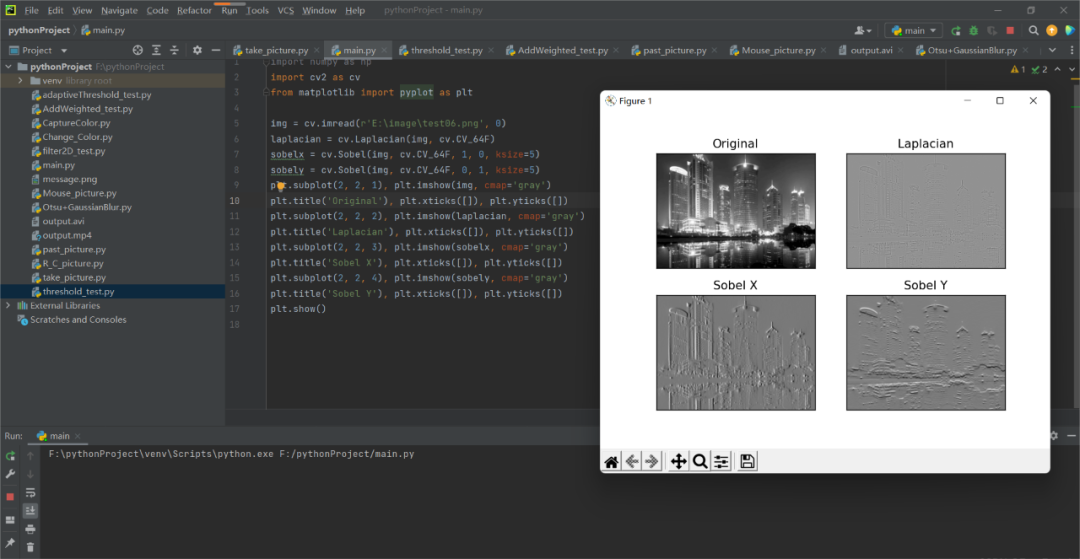
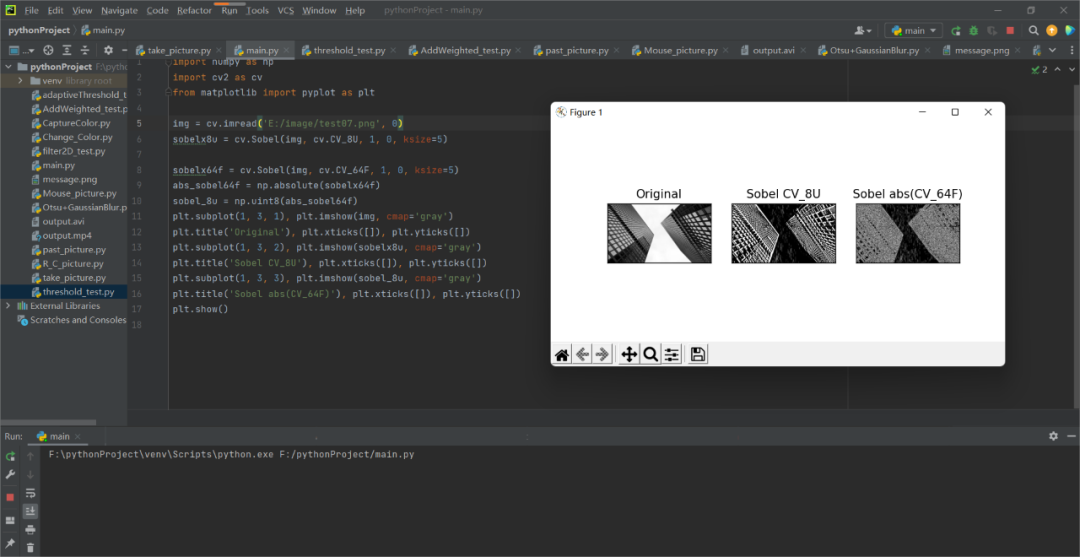
注意：在上面的實例中，輸出的數據類型為cv.CV_8U或np.uint8，問題就出在這里，黑色到白色的過渡被視為正斜率（具有正值），而白色到黑色的過渡被視為負斜率（具有負值），當我們將數據轉換為np.uint8時，所有負斜率均設為零，意思就是我們會錯過這一邊緣信息

當要檢測兩個邊緣，更好的選擇是將輸出數據類型保留為更高的形式，取其絕對值然后再轉回cv.CV_8U

這是一個必較重要且不容忽略的問題，所以我們再通過一個例子來看看

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('E:/image/test07.png', 0)
sobelx8u = cv.Sobel(img, cv.CV_8U, 1, 0, ksize=5)

sobelx64f = cv.Sobel(img, cv.CV_64F, 1, 0, ksize=5)
abs_sobel64f = np.absolute(sobelx64f)
sobel_8u = np.uint8(abs_sobel64f)
plt.subplot(1, 3, 1), plt.imshow(img, cmap='gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 3, 2), plt.imshow(sobelx8u, cmap='gray')
plt.title('Sobel CV_8U'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 3, 3), plt.imshow(sobel_8u, cmap='gray')
plt.title('Sobel abs(CV_64F)'), plt.xticks([]), plt.yticks([])
plt.show()

2. Canny邊緣檢測

Canny Edge Detection是由John F. Canny發明的一種流行的邊緣檢測算法，這是一個多階段，主要分為：高斯濾波、梯度計算、非極大值抑制和雙閾值檢測

2.1 多階段的Canny邊緣檢測算法

高斯濾波（降噪）

由于邊緣檢測很容易收到圖像中噪聲的影響，因此我們通過Canny邊緣檢測算法進行圖像處理時第一步是使用5x5高斯濾波器消除圖像中的噪聲

高斯濾波的具體方法是生成一個高斯模板，使用卷積進行時進行時域濾波

梯度計算

使用Sobel核在水平和垂直方向上對平滑圖像進行濾波，以在水平和垂直方向得到一階導數

非極大值抑制

在獲得梯度大小和方向后，將對圖像進行全面掃描，以去除可能不構成邊緣的所有不需要的像素，為此在每個像素處檢查像素是都是在其梯度方向上附近的局部最大值

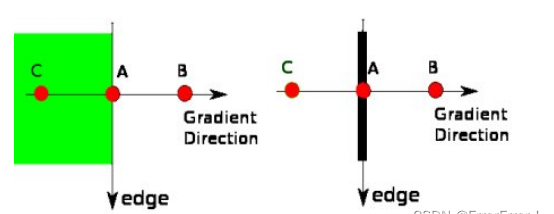
點A在邊緣（垂直方向）上。漸變方向垂直于邊緣。點B和C在梯度方向上。因此，將A點與B點和C點進行檢查，看是否形成局部最大值。如果是這樣，則考慮將其用于下一階段，否則將其抑制（置為零）。簡而言之，你得到的結果是帶有“細邊”的二進制圖像

磁滯閾值（雙閾值檢測）

在這個階段會確定哪些邊緣是真正的邊緣，為此我們需要提供兩個閾值minVal和maxVal，強度梯度大于maxVal的任何邊緣必定是邊緣，而小于minVal的任何邊緣必定不是邊緣，如果講他們連接到邊緣像素。則將他們視為邊緣的一部分否則將被丟棄

邊緣A在maxVal上，因此被視為“確定邊緣”，盡管C低于minVal但它連接到A，因此被視為有效便，我們得到了完整的曲線

但是盡管B在minVal上并且與C處于統一區域，但是它沒有連接到任何確保邊緣，因此它也會丟棄

注意：我們必須選擇相應的minVal和maxVal才能獲取正確的結果

2.2 OpenCV中的Canny Edge檢測

OpenCV將Canny邊緣檢測算法的四個階段放在了一個單數cv.Canny()中，我們只需要去正確使用它就能獲取我們的邊緣檢測需求

我們看看cv.Canny()這個函數的傳參，第一個參數是圖像資源，第二、三個參數分別是用于磁滯閾值（雙閾值檢測）階段的兩個閾值minVal和maxVal，第四個參數是picture_size，它用于查找圖像漸變的Sobel內核的大小，默認為3，第五個參數是L2gradient，它指定用于查找梯度的方程式，若為True會使用更精確的公式，若為False則用默認

我們通過一個例子來看看

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('E:/image/test08.png', 0)
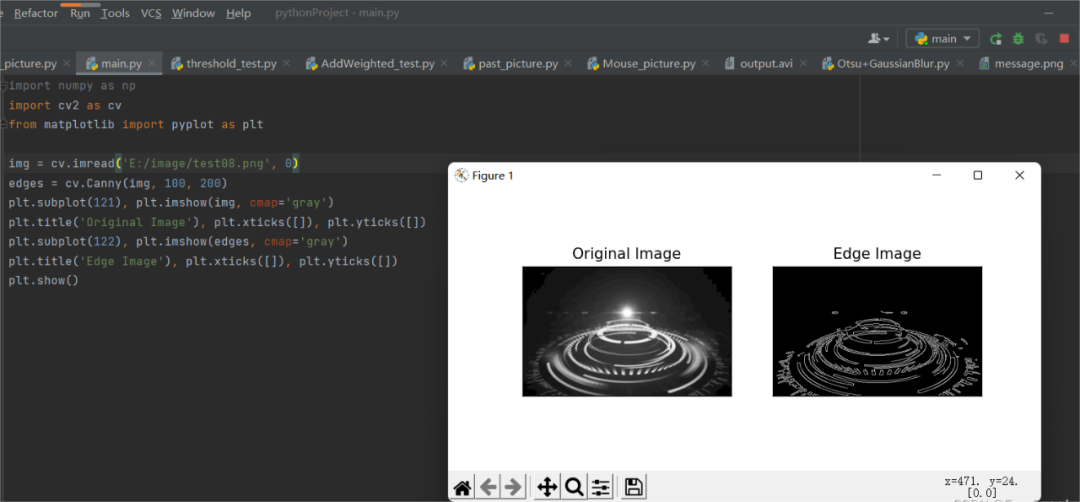
edges = cv.Canny(img, 100, 200)
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(edges, cmap='gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([])
plt.show()

3. 圖像金字塔

3.1 金字塔理論基礎

在之前我們學習的內容中，使用的都是像素大小恒定不變的圖像，但是在一些情況下，我們在處理圖像時不知道我們所需要的物體的具體尺寸（或物體是以什么樣的尺寸出現在圖像中）

在這種情況下我們需要創建一組具有不同分辨率的相同圖像，并在這些圖像中搜索目標對象，這些具有不同像素大小的圖像集就是我們的圖像金字塔

因為當它們堆疊在底部時，最高分辨率的圖像位于頂部，最低分辨率的圖像位于頂部時，看起來像金字塔

一般來說有兩種金字塔：高斯金字塔和拉普拉斯金字塔

3.1.1 高斯金字塔

高斯金字塔中的較高級別（低分辨率）是通過先用高斯核對圖像進行卷積再刪除偶數行和列，然后較高級別的每個像素由基礎級別的5個像素的貢獻與高斯權重形成，通過這樣的操作M x N的圖像變為M/2 x N/2圖像,因此面積減少到原來的四分之一，我們稱之為Octave，當我們的金字塔越靠上時這種模式就越繼續。

向下采樣方法：1.對圖像進行高斯內核卷積；2.將所有偶數行和列去除

圖像的較低級別（高分辨率）是通過較高級別（低分辨率）在每個維度上擴大為原來的兩倍，新增的行和列（偶數行和列）以0填充，然后使用指定的濾波器進行卷積去估計丟失像素的近似值。

向上采樣方法：1.將圖像在每個維度擴大到原來的兩倍，以新增的行和列以0填充；2.使用原先同樣的內核（x4）與方法后的圖像卷積，獲得新增像素的近似值在縮放過程中已經丟失了一些信息，如果想在縮放過程中減少信息的丟失，就需要用到拉普拉斯金字塔

cv.pyrUp(src)函數：其中只需要傳入一個參數，代表圖像資源，用于對圖像做向上采樣

cv.pyrDown()函數：參數傳遞與cv.pyrUp()一致，用于對圖像做向下采樣，通常也可以做圖像模糊化處理

3.1.2 拉普拉斯金字塔

拉普拉斯金字塔由高斯金字塔形成，沒有專用的功能，拉普拉斯金字塔圖像僅表示邊緣圖像，它的大多數元素為0，它們通常用于圖像壓縮

拉普拉斯金字塔的層由高斯金字塔的層與高斯金字塔的高層的擴展版本之間的差形成

我們通過一個例子來展示拉普拉斯金字塔

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread(r'E:image	est06.png', )
loser_reso = cv.pyrDown(img)
higher_reso = cv.pyrUp(loser_reso)
lapPyr = img - higher_reso
test = higher_reso
loser_reso2 = cv.pyrDown(test)
higher_reso2 = cv.pyrUp(loser_reso2)
lapPyr2 = test - higher_reso2
cv.imshow('lapPyr', lapPyr)
cv.imshow('lapPyr2', lapPyr2)
cv.waitKey(0)
cv.destroyAllWindows()

3.2 使用圖像金字塔進制圖像融合

圖像金字塔的一個應用是圖像融合，如果進行簡單的圖像拼接，我們將兩個圖片堆疊在一起，會因為圖像之間的不連續性看起來效果不好，在這種情況下金字塔混合圖像可以無縫混合，而不會在圖像中保留大量數據

想要達到圖像混合的效果，需要完成以下步驟：

加載兩個需要進行混合的圖像

查找兩張圖像的高斯金字塔，然后在其高斯金字塔中找到其拉普拉斯金字塔

在每個拉普拉斯金字塔級別中加入兩張圖片的各一半

最后從此聯合圖像金字塔中重建原始圖像

import cv2 as cv
import numpy as np, sys

A = cv.imread('E:/image/horse.png')
B = cv.imread('E:/image/cow.png')
# 生成A的高斯金字塔
G = A.copy()
gpA = [G]
for i in range(6):
    G = cv.pyrDown(G)
    gpA.append(G)
# 生成B的高斯金字塔
G = B.copy()
gpB = [G]
for i in range(6):
    G = cv.pyrDown(G)
    gpB.append(G)
# 生成A的拉普拉斯金字塔
lpA = [gpA[5]]
for i in range(5, 0, -1):
    GE = cv.pyrUp(gpA[i])
    L = cv.subtract(gpA[i - 1], GE)
    lpA.append(L)
# 生成B的拉普拉斯金字塔
lpB = [gpB[5]]
for i in range(5, 0, -1):
    GE = cv.pyrUp(gpB[i])
    L = cv.subtract(gpB[i - 1], GE)
    lpB.append(L)
# 現在在每個級別中添加左右兩半圖像
LS = []
for la, lb in zip(lpA, lpB):
    rows, cols, dpt = la.shape
    ls = np.hstack((la[:, 0:cols / 2], lb[:, cols / 2:]))
    LS.append(ls)
# 現在重建
ls_ = LS[0]
for i in range(1, 6):
    ls_ = cv.pyrUp(ls_)
    ls_ = cv.add(ls_, LS[i])
# 圖像與直接連接的每一半
real = np.hstack((A[:, :cols / 2], B[:, cols / 2:]))
cv.imwrite('Pyramid_blending2.jpg', ls_)
cv.imwrite('Direct_blending.jpg', real)

編輯：黃飛