什么是一致性模型?
在分布式系統(tǒng)中,C(一致性) 和 A(可用性)始終存在矛盾。若想保證可用性,就必須通過(guò)復(fù)制、分片等方式冗余存儲(chǔ)。而一旦進(jìn)行復(fù)制,又來(lái)帶多副本數(shù)據(jù)一致性的問(wèn)題——一個(gè)副本的數(shù)據(jù)更新之后,其他副本必須要保持同步,否則數(shù)據(jù)不一致就可能導(dǎo)致業(yè)務(wù)出現(xiàn)問(wèn)題。
因此,每次更新數(shù)據(jù)對(duì)所有副本進(jìn)行修改的時(shí)間以及方式?jīng)Q定了復(fù)制代價(jià)的大小。全局同步與性能實(shí)際上是矛盾的,而為了提高性能,往往會(huì)采用放寬一致性要求的方法。因此,我們需要用一致性模型來(lái)理解和推理在分布式系統(tǒng)中數(shù)據(jù)復(fù)制需要考慮的問(wèn)題和基本假設(shè)。
那么什么是一致性模型呢?
一致性模型本質(zhì)上是進(jìn)程與數(shù)據(jù)存儲(chǔ)的約定:如果進(jìn)程遵循某些規(guī)則,那么進(jìn)程對(duì)數(shù)據(jù)的讀寫操作都是可預(yù)期的。
下圖即為 Jepsen 概括的常見(jiàn)的一致性模型:
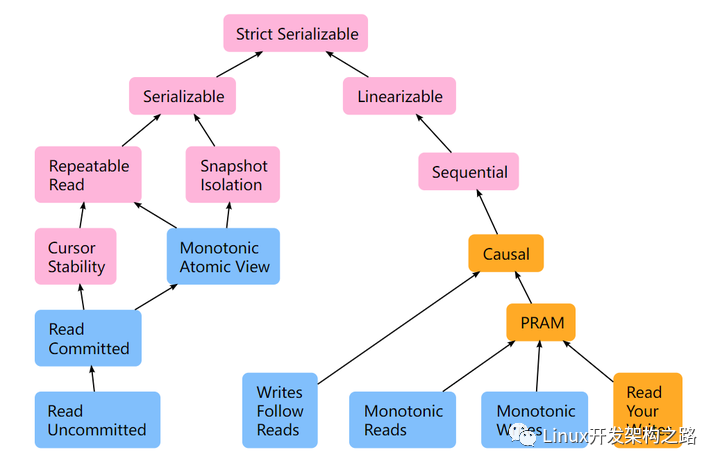
不可用(Unavailable):粉色代表網(wǎng)絡(luò)分區(qū)后完全不可用。當(dāng)出現(xiàn)網(wǎng)絡(luò)隔離等問(wèn)題的時(shí)候,為了保證數(shù)據(jù)的一致性,不提供服務(wù)。熟悉 CAP 理論的同學(xué)應(yīng)該清楚,這就是典型的 CP 系統(tǒng)了。
- 嚴(yán)格可用 (Sticky Available):黃色代表嚴(yán)格可用。即使一些節(jié)點(diǎn)出現(xiàn)問(wèn)題,在一些還沒(méi)出現(xiàn)故障的節(jié)點(diǎn),仍然保證可用,但需要保證 client 的操作是一致的。
- 完全可用(Highly Available):藍(lán)色代表完全可用。就是網(wǎng)絡(luò)全掛掉,在沒(méi)有出現(xiàn)問(wèn)題的節(jié)點(diǎn)上面,仍然可用。
一致性模型主要可以分為兩類:能夠保證所有進(jìn)程對(duì)數(shù)據(jù)的讀寫順序都保持一致的一致性模型稱為強(qiáng)一致性模型,而不能保證的一致性模型稱為弱一致性模型。
強(qiáng)一致性模型
強(qiáng)一致性包含線性一致性和順序一致性,其中前者對(duì)安全性的約束更強(qiáng),也是分布式系統(tǒng)中能保證的最好的一致性。
線性一致性(Linearizable Consistency)
線性一致性是最嚴(yán)格的且可實(shí)現(xiàn)的單對(duì)象單操作一致性模型。在這種模型下,寫入的值在調(diào)用和完成之間的某個(gè)時(shí)間點(diǎn)可以被其他節(jié)點(diǎn)讀取出來(lái)。且所有節(jié)點(diǎn)讀到數(shù)據(jù)都是原子的,即不會(huì)讀到數(shù)據(jù)轉(zhuǎn)換的過(guò)程和中間未完成的狀態(tài)。
要想達(dá)到線性一致,需要滿足以下條件:
- 任何一次讀都能讀取到某個(gè)數(shù)據(jù)最近的一次寫的數(shù)據(jù)。
- 所有進(jìn)程看到的操作順序都跟全局時(shí)鐘下的順序一致。
- 所有進(jìn)程都按照全局時(shí)鐘的時(shí)間戳來(lái)區(qū)分事件的先后,那么必然所有進(jìn)程看到的數(shù)據(jù)讀寫操作順序一定是一樣的
我們發(fā)現(xiàn),這個(gè)要求十分苛刻,難以在現(xiàn)實(shí)中實(shí)現(xiàn)。因?yàn)楦鞣N物理限制使分布式數(shù)據(jù)不可能一瞬間去同步這種變化。(通信是必然有延遲的,一旦有延遲,時(shí)鐘的同步就沒(méi)法做到一致。)
順序一致性(Sequential Consistency)
由于線性一致的代價(jià)高昂,因此人們想到,既然全局時(shí)鐘導(dǎo)致嚴(yán)格一致性很難實(shí)現(xiàn),那么我們能否放棄了全局時(shí)鐘的約束,改為分布式邏輯時(shí)鐘實(shí)現(xiàn)呢?
Lamport 在 1979 年就提出的順序一致性正是基于上述原理。順序一致性中所有的進(jìn)程以相同的順序看到所有的修改。讀操作未必能及時(shí)得到此前其他進(jìn)程對(duì)同一數(shù)據(jù)的寫更新,但是每個(gè)進(jìn)程讀到的該數(shù)據(jù)的不同值的順序是一致的。
其需要滿足以下條件:
- 任何一次讀寫操作都是按照某種特定的順序。
- 所有進(jìn)程看到的讀寫操作順序都保持一致。
我們發(fā)現(xiàn)他們都能夠保證所有進(jìn)程對(duì)數(shù)據(jù)的讀寫順序保持一致。那么它與線性一致性有什么不同呢?
盡管順序一致性通過(guò)邏輯時(shí)鐘保證所有進(jìn)程保持一致的讀寫操作順序,但這些讀寫操作的順序跟實(shí)際上發(fā)生的順序并不一定一致。而線性一致性是嚴(yán)格保證跟實(shí)際發(fā)生的順序一致的。
我們以下圖為例:

例子1:線性一致性與順序一致性的區(qū)別
圖 a 滿足了順序一致性,但未滿足線性一致性。 從全局時(shí)鐘來(lái)看,p2 的 read(x,0) 在 p1 的 write(x,4) 之后,但是 p1 卻讀出了舊的數(shù)據(jù)。因此不滿足線性一致性。但是兩個(gè)進(jìn)程各自的讀寫順序卻是合理的,進(jìn)程之間也沒(méi)有產(chǎn)生沖突,因此從這兩個(gè)進(jìn)程的視角來(lái)看,執(zhí)行流程是這樣的 write(y,2)、read(x,0)、 write(x,4)、read(y,2)。此時(shí)滿足順序一致性。
- 圖 b 滿足線性一致性。 因?yàn)槊總€(gè)讀操作都讀到了該變量的最新寫的結(jié)果,同時(shí)兩個(gè)進(jìn)程看到的操作順序與全局時(shí)鐘的順序一樣。
- 圖 c 不滿足順序一致性。 因?yàn)閺倪M(jìn)程 P1 的角度看,它對(duì)變量 y 的讀操作返回了結(jié)果 0。那么就是說(shuō),P1 進(jìn)程的對(duì)變量 y 的讀操作在 P2 進(jìn)程對(duì)變量 y 的寫操作之前,x 變量也如此。此時(shí)兩個(gè)進(jìn)程存在沖突,因此這個(gè)順序不滿足順序一致性。
弱一致性模型
弱一致性是指系統(tǒng)在數(shù)據(jù)成功寫入之后,不承諾立即可以讀到最新寫入的值,也不會(huì)具體承諾多久讀到,但是會(huì)盡可能保證在某個(gè)時(shí)間級(jí)別之后,可以讓數(shù)據(jù)達(dá)到一致性狀態(tài)。其中包含因果一致性和最終一致性、客戶端一致性。
因果一致性(Causal Consistency)
什么是因果關(guān)系呢?
如果事件 B 是由事件 A 引起的或者受事件 A 的影響,那么這兩個(gè)事件就具有因果關(guān)系。
因果一致性是一種弱化的順序一致性模型,它僅要求有因果關(guān)系的操作順序是一致的,沒(méi)有因果關(guān)系的操作順序是隨機(jī)的。
因果一致性的條件包括:
- 所有進(jìn)程必須以相同的順序看到具有因果關(guān)系的讀寫操作。
- 不同進(jìn)程可以以不同的順序看到并發(fā)的讀寫操作。
我們?nèi)绾未_定是否具有因果關(guān)系呢?如何傳播這些因果關(guān)系呢?
即通過(guò)邏輯時(shí)鐘來(lái)保證兩個(gè)寫入是有因果關(guān)系的。而實(shí)現(xiàn)這個(gè)邏輯時(shí)鐘的一種主要方式就是向量時(shí)鐘。向量時(shí)鐘算法利用了向量這種數(shù)據(jù)結(jié)構(gòu),將全局各個(gè)進(jìn)程的邏輯時(shí)間戳廣播給所有進(jìn)程,每個(gè)進(jìn)程發(fā)送事件時(shí)都會(huì)將當(dāng)前進(jìn)程已知的所有進(jìn)程時(shí)間寫入到一個(gè)向量中,而后進(jìn)行傳播。
最終一致性(Eventual Consistency)
最終一致性是更加弱化的一致性模型,它被表述為副本之間的數(shù)據(jù)復(fù)制完全是異步的,如果數(shù)據(jù)停止修改,那么副本之間最終會(huì)完全一致。而這個(gè)最終可能是數(shù)毫秒到數(shù)天,乃至數(shù)月,甚至是“永遠(yuǎn)”。
對(duì)于最終一致性,我們主要關(guān)注以下兩點(diǎn):
- **最終是多久。**通常來(lái)說(shuō),實(shí)際運(yùn)行的系統(tǒng)需要能夠保證提供一個(gè)有下限的時(shí)間范圍。
- **并發(fā)沖突如何解決。**一段時(shí)間內(nèi)可能數(shù)據(jù)可能多次更新,到底以哪個(gè)數(shù)據(jù)為準(zhǔn)?通常采用最后寫入成功或向量時(shí)鐘等策略。
因?yàn)樵跀?shù)據(jù)寫入與讀取完全不考慮別的約束條件,因此最終一致性具有最高的并發(fā)度,經(jīng)常被應(yīng)用于對(duì)性能要求高的場(chǎng)景中。
客戶端一致性(Client-centric Consistency)
在最終一致性的模型中,如果客戶端在數(shù)據(jù)不同步的時(shí)間窗口內(nèi)訪問(wèn)不同的副本的同一個(gè)數(shù)據(jù),會(huì)出現(xiàn)讀取同一個(gè)數(shù)據(jù)卻得到不同的值的情況。為了解決這個(gè)問(wèn)題,有人提出了以客戶端為中心的一致性模型。
客戶端一致性是站在一個(gè)客戶端的角度來(lái)觀察系統(tǒng)的一致性。其保證該客戶端對(duì)數(shù)據(jù)存儲(chǔ)的訪問(wèn)的一致性,但是它不為不同客戶端的并發(fā)訪問(wèn)提供任何一致性保證。
分布式數(shù)據(jù)庫(kù)中,一個(gè)節(jié)點(diǎn)很可能同時(shí)連接到多個(gè)副本中,復(fù)制的延遲性會(huì)造成它從不同副本讀取數(shù)據(jù)是不一致的。而客戶端一致性就是為了定義并解決這個(gè)問(wèn)題而存在的,這其中包含了寫跟隨讀、管道隨機(jī)訪問(wèn)存儲(chǔ)兩大類別。
寫跟隨讀(Writes-Follow-Reads Consistency)
寫跟隨讀的另一個(gè)名字是回話因果(session causal)。可以看到它與因果一致的區(qū)別是,它只針對(duì)一個(gè)客戶端。 即對(duì)于一個(gè)客戶端,如果一次讀取到了寫入的值 V1,那么這次讀取之后寫入了 V2。從其他節(jié)點(diǎn)看,寫入順序一定是 V1、V2。
管道隨機(jī)訪問(wèn)存儲(chǔ)(PRAM,Pipeline Random Access Memory)
管道隨機(jī)訪問(wèn)存儲(chǔ)的名字來(lái)源于共享內(nèi)存訪問(wèn)模型。其對(duì)于單個(gè)進(jìn)程的寫操作都被觀察到是順序的,但不同的進(jìn)程寫會(huì)觀察到不同的順序。
其可拆解為以下三種一致性:
- 單調(diào)讀一致性(Monotonic-read Consistency):它強(qiáng)調(diào)一個(gè)值被讀取出來(lái),那么后續(xù)任何讀取都會(huì)讀到該值,或該值之后的值,而不會(huì)讀取到舊值。
- 單調(diào)寫一致性(Monotonic-write Consistency):如果從一個(gè)節(jié)點(diǎn)寫入兩個(gè)值,它們的執(zhí)行順序是 V1、V2。那么從任何節(jié)點(diǎn)觀察它們的執(zhí)行順序都應(yīng)該是 V1、V2。
- 讀你所寫一致性(Read-your-writes Consistency):一個(gè)節(jié)點(diǎn)寫入數(shù)據(jù)后,在該節(jié)點(diǎn)或其他節(jié)點(diǎn)上是一定能讀取到這個(gè)數(shù)據(jù)的。
能夠同時(shí)滿足以上三種一致性的即為滿足 PRAM。
PRAM、因果一致、線性一致到底有什么區(qū)別呢?

例子2:因果一致、順序一致、PRAM 的區(qū)別
圖 a 滿足了順序一致性與因果一致性。 圖上的進(jìn)程都滿足相同的順序與因果關(guān)系,因此滿足順序一致性與因果一致性。
- 圖 b 滿足了因果一致性,但未滿足順序一致性。 對(duì)于進(jìn)程 p3 和 p4 其看到的 p1 和 p2 的執(zhí)行順序不一致,因此不滿足順序一致性。但是由于 p1 與 p2 的寫入沒(méi)有任何因果關(guān)系,所以此時(shí)滿足因果一致性。
- 圖 c 滿足了 PRAM,但未滿足因果一致性。 由于 p2 的 r(x,4) 依賴于 p1 的 w(x,4),此時(shí)兩者存在因果關(guān)系。然而對(duì)于進(jìn)程 p3 和 p4 而言,其看到的 p1 和 p2 執(zhí)行順序不同,因此此時(shí)并不滿足因果一致性。但此時(shí)我們?cè)賮?lái)分析它們的觀察順序,此時(shí) p4 觀察的到順序是 w(x.7)、w(x,2)、w(x,4)。而 p3 觀察到的是 w(x,2)、w(x,4)、w(x,7)。盡管此時(shí)它們對(duì)不同進(jìn)程寫操作觀察的順序不同,但是對(duì)于同一個(gè)進(jìn)程的寫操作觀察順序是一致的,因此其滿足 PRAM 一致性。
下圖即為上面討論的幾種一致性模型的關(guān)系:

一致性模型之間的關(guān)系
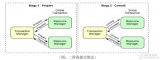
事務(wù)隔離性
在一開始那張一致性模型圖中,其實(shí)是有兩個(gè)分支的,一個(gè)對(duì)應(yīng)的就是數(shù)據(jù)庫(kù)里面的隔離性(Isolation),另一個(gè)其實(shí)對(duì)應(yīng)的是分布式系統(tǒng)的一致性(Consistency)。
事務(wù)隔離是描述并行事務(wù)之間的行為,而一致性是描述非并行事務(wù)之間的行為。其實(shí)廣義的事務(wù)隔離應(yīng)該是經(jīng)典隔離理論與一致性模型的一種混合。
潛在問(wèn)題
如下即數(shù)據(jù)庫(kù)實(shí)現(xiàn)中遇到的各種各樣的 isolation 問(wèn)題。
- P0 Dirty Write(臟寫):一個(gè)事務(wù)修改了另一個(gè)尚未提交的事務(wù)已經(jīng)修改的值。
- P1 Dirty Read(臟讀):一個(gè)事務(wù)讀取到了另一個(gè)執(zhí)行到一半的事務(wù)中修改的值。
- P2 Non-Repeatable Read(不可重復(fù)讀):一個(gè)事務(wù)讀取過(guò)程中讀到了另一個(gè)事務(wù)更新后的結(jié)果。
- P3 Phantom(幻讀):某一事務(wù) A 先挑選出了符合一定條件的數(shù)據(jù),之后另一個(gè)事務(wù) B 修改了符合該條件的數(shù)據(jù),此時(shí) A 再進(jìn)行的操作都是基于舊的數(shù)據(jù),從而產(chǎn)生不一致。
- P4 Lost Update(丟失更新):更新被另一個(gè)事務(wù)覆蓋。
- P4C Cursor Lost Update(游標(biāo)丟失更新):與 Lost Update 類似,只是發(fā)生于 cursor 的操作過(guò)程之中。
- A5A Read Skew(讀傾斜):由于事務(wù)的交叉導(dǎo)致讀取到了不一致的數(shù)據(jù)。
- A5B Write Skew(寫傾斜):兩個(gè)事務(wù)同時(shí)讀取到了一致的數(shù)據(jù),然后分別進(jìn)行了滿足條件的修改,但最終結(jié)果破壞了一致性。
隔離級(jí)別
對(duì)于分布式數(shù)據(jù)庫(kù)來(lái)說(shuō),原始的隔離級(jí)別并沒(méi)有舍棄,而是引入了一致性模型后,擴(kuò)寬數(shù)據(jù)庫(kù)隔離級(jí)別的內(nèi)涵。其中共有如下數(shù)種隔離級(jí)別:
- Read Uncommitted(讀未提交):事務(wù)執(zhí)行過(guò)程中能夠讀到未提交的修改。
- Read Committed(讀已提交):事務(wù)執(zhí)行過(guò)程中能夠讀到已提交的修改。
- Monotonic Atomic View(單調(diào)原子視圖):在 Read Committed 的基礎(chǔ)上加上了原子性的約束,觀測(cè)到其他事務(wù)的修改時(shí)會(huì)觀察到完整的修改。
- Cursor Stability(穩(wěn)定游標(biāo)):使用 cursor 讀取某個(gè)數(shù)據(jù)時(shí),這個(gè)不能被其他事務(wù)修改直至 cursor 釋放或事務(wù)結(jié)束。
- Snapshot Isolation(快照隔離級(jí)別):即使其他事務(wù)修改了數(shù)據(jù),重復(fù)讀取都會(huì)讀到一樣的數(shù)據(jù)。
- Repeatable Read(可重復(fù)讀):每個(gè)事務(wù)在獨(dú)立、一致的 snapshot 上進(jìn)行操作,直至提交后其他事務(wù)才可見(jiàn)。
- Serializable(串行化):事務(wù)按照一定的次序順序執(zhí)行。
對(duì)應(yīng)的可能發(fā)生的問(wèn)題如下

P(Possible):會(huì)發(fā)生。
- SP(Sometimes Possible):有時(shí)候可能發(fā)生。
- NP(Not Possible):不可能發(fā)生。
-
數(shù)據(jù)存儲(chǔ)
+關(guān)注
關(guān)注
5文章
977瀏覽量
50959 -
模型
+關(guān)注
關(guān)注
1文章
3268瀏覽量
48924 -
分布式系統(tǒng)
+關(guān)注
關(guān)注
0文章
146瀏覽量
19276
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
一致性測(cè)試系統(tǒng)的技術(shù)原理和也應(yīng)用場(chǎng)景
一行代碼,保障分布式事務(wù)一致性—GTS:微服務(wù)架構(gòu)下分布式事務(wù)解決方案
順序一致性和TSO一致性分別是什么?SC和TSO到底哪個(gè)好?
藍(lán)鯨集群文件系統(tǒng)中資源交互一致性協(xié)議
分布式一致性算法Yac
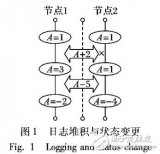
基于消息通信的分布式系統(tǒng)最終一致性平臺(tái)

DSA系統(tǒng)的全局一致性需求分析
分布式大數(shù)據(jù)不一致性檢測(cè)
一致性哈希是什么?為什么它是可擴(kuò)展的分布式系統(tǒng)架構(gòu)的一個(gè)必要工具
分布式系統(tǒng)的CAP和數(shù)據(jù)一致性模型
基于自觸發(fā)一致性算法的分布式分層控制策略
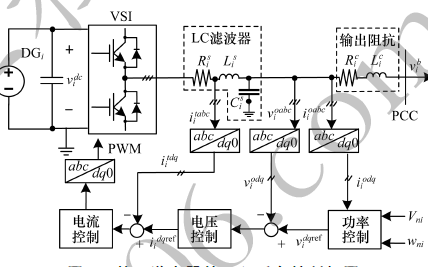
一種更安全的分布式一致性算法選舉機(jī)制





 分布式系統(tǒng)中常見(jiàn)的一致性模型
分布式系統(tǒng)中常見(jiàn)的一致性模型










評(píng)論