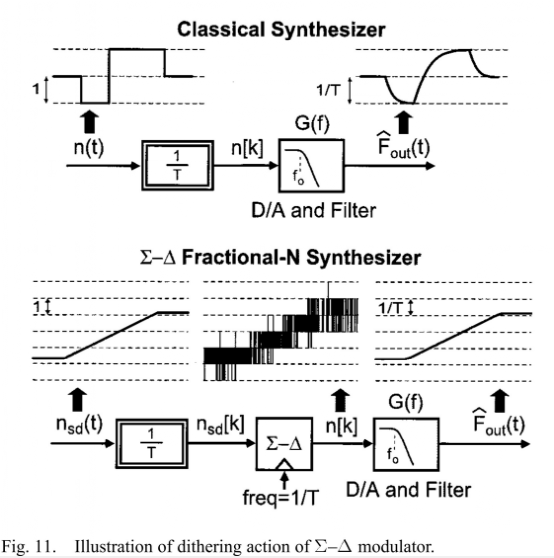
為了理解Σ-Δ調(diào)制器在頻率綜合器中究竟引起了啥影響,圖11可以比較好的說明。需要指出的是,圖11中把分頻比的變化看作一個(gè)連續(xù)信號(hào),這樣的話能夠比較好的在1/T的采樣情況下,實(shí)現(xiàn)一個(gè)單位的輸入變化(單位是分頻比的code),反映到1/T的輸出變化(范圍是Hz)(1/T的縮放因子是采樣導(dǎo)致的),以便使模型與真實(shí)情況一致。
在經(jīng)典情況中,分頻比是不變的,除非輸出頻率變化。而當(dāng)分頻比變化時(shí),由于pll本征的低通特性,所以輸出頻率的變化相比于分頻比變化的輸入而言就好像經(jīng)過了低通濾波器一樣。
然而對(duì)于Σ-Δ小數(shù)N分頻的頻率綜合器而言,分頻比的變化頻率非常高,而環(huán)路傳輸函數(shù)會(huì)提取出其中的低頻成分,與Σ-Δ的輸入信號(hào)nsd(t)一致(幾乎可以達(dá)到任意高的精度)。
所以,頻率調(diào)制精度與ref的頻率無關(guān),不過ref的頻率越高,其達(dá)到指定頻率精度的速度越快。
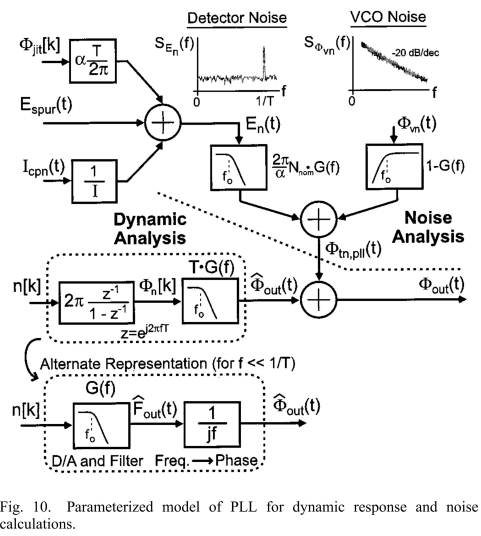
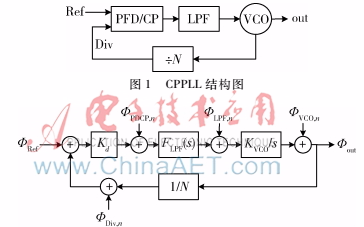
基于圖10的頻域模型(是根據(jù)前一篇推文中的時(shí)域模型轉(zhuǎn)化而來:Z變換,S變換),我們添加上Σ-Δ的影響。量化噪聲我們認(rèn)為是白色的。
*Comments:圖10中,G(f)T中的T從哪里來?這里fig表達(dá)的是分頻比序列n[k]到輸出的影響,所以從離散域進(jìn)入連續(xù)域需要乘一個(gè)采樣周期T,具體法則可以看下圖:

首先,我們可以看到Σ-Δ的量化噪聲逐次通過數(shù)字累加器、pll環(huán)路傳遞函數(shù)到pll的相位輸出。數(shù)字累加器模型來源于分頻器的積分效果,將Σ-Δ的噪聲整形階數(shù)降低了一階(?可以認(rèn)為Σ-Δ僅僅是提供了一個(gè)分頻比上的一個(gè)抖動(dòng),分頻比如果想要影響到相位,必然是要經(jīng)過一個(gè)積分的)
Pll的傳遞函數(shù)的效果主要是作為一個(gè)低通濾波器,濾掉了高頻的量化噪聲。Σ-Δ的量化噪聲在環(huán)路中提供了一個(gè)額外的噪聲源。
不過他的出現(xiàn)并沒有影響原有的各個(gè)噪聲源到輸出的影響并沒有改變。(僅取決于環(huán)路傳遞函數(shù)和歸一化分頻數(shù)Nnorminal)
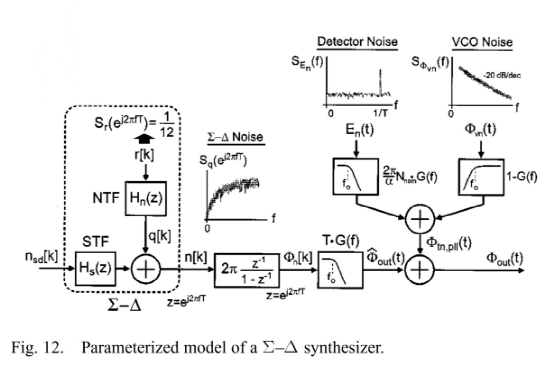
現(xiàn)在,pll輸出的相位噪聲貢獻(xiàn)可以分為三部分:pfd+cp、VCO、Σ-Δ量化噪聲(分頻器對(duì)pn影響很小,假設(shè)不會(huì)引入噪聲)根據(jù)圖12,我們可以直接寫出量化噪聲與pll輸出位置相位噪聲的關(guān)系式:
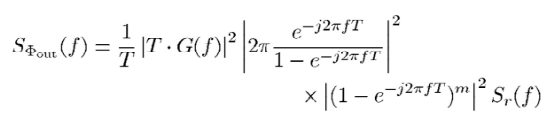
整理得到
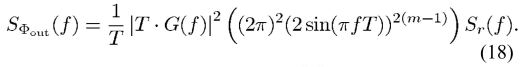
(事實(shí)上,對(duì)于一些輸入而言,量化噪聲并不是白色的,之后的深入理解Σ-Δ系列推送會(huì)有說明)如果量化噪聲是白色的,那么其譜密度應(yīng)當(dāng)是1/12,這里量化臺(tái)階認(rèn)為是1。(量化臺(tái)階為1在這里的意思就是實(shí)際控制分頻器進(jìn)行分頻,分頻比僅有兩種選擇)
事實(shí)上,18式已經(jīng)可以觀察到,Σ-Δ的NTF被削弱了一級(jí),原因是分頻器的積分效果。如果量化噪聲真的可以被認(rèn)為是白色的,那么量化噪聲譜密度體現(xiàn)在pll的輸出應(yīng)當(dāng)為(m-1)*20dB/dec的斜率上升。(當(dāng)然前提是頻率遠(yuǎn)小于采樣頻率)
所以這里就是為什么很多設(shè)計(jì)中使Σ-Δ的階數(shù)與pll的階數(shù)相同,因?yàn)閜ll的階數(shù)事實(shí)上體現(xiàn)在g(f)的分母上,這樣就可以抵消掉后面的Σ-Δ調(diào)制因式,還能多出來一個(gè)次數(shù),換句話說,能夠有效抑制高頻的量化噪聲。
具體在輸出應(yīng)當(dāng)體現(xiàn)為-20dB/dec的滾降。這個(gè)滾降特性和VCO是一樣的,能夠不浪費(fèi),又夠用,是比較恰當(dāng)?shù)脑O(shè)計(jì)考慮。
Comments:這里Σ-Δ的采樣頻率認(rèn)為跟ref一樣,如果不一樣的,能否提高Σ-Δ的采樣頻率?收益如何?

-
低通濾波器
+關(guān)注
關(guān)注
14文章
486瀏覽量
47808 -
分頻器
+關(guān)注
關(guān)注
43文章
452瀏覽量
50513 -
調(diào)制器
+關(guān)注
關(guān)注
3文章
880瀏覽量
45719 -
累加器
+關(guān)注
關(guān)注
0文章
50瀏覽量
9568 -
PLL電路
+關(guān)注
關(guān)注
0文章
92瀏覽量
6622
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
全數(shù)字鎖相環(huán)的設(shè)計(jì)及分析
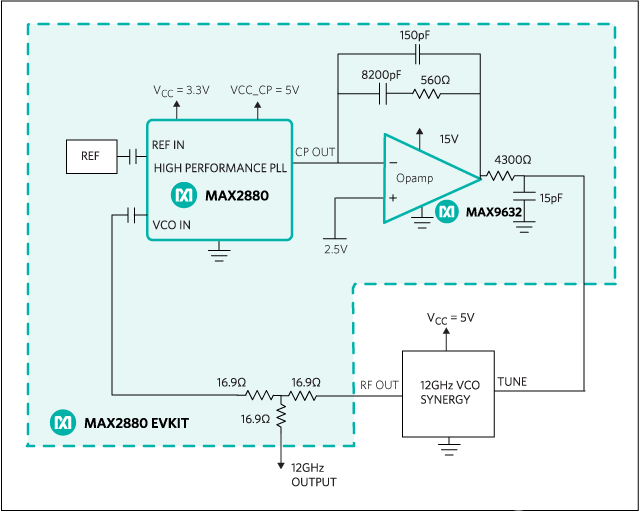
怎么設(shè)計(jì)低噪聲12 GHz微波小數(shù)N分頻鎖相環(huán)?
鎖相環(huán)相位噪聲與環(huán)路帶寬的關(guān)系是什么
小數(shù)分頻鎖相環(huán)的工作原理
低噪聲小數(shù)N分頻鎖相環(huán)實(shí)現(xiàn)方案
小數(shù)N分頻鎖相環(huán)應(yīng)用優(yōu)缺點(diǎn)分析
鎖相環(huán)相位噪聲與環(huán)路帶寬的關(guān)系分析
低噪聲12 GHz微波小數(shù)N分頻鎖相環(huán)的設(shè)計(jì)

關(guān)于2.4 GHz的低噪聲亞采樣鎖相環(huán)設(shè)計(jì)
Delta-Sigma小數(shù)鎖相環(huán)的邏輯及特性
新型的采用電流轉(zhuǎn)向電荷泵的快速鎖定小數(shù)分頻鎖相環(huán)
12GHz、超低相位噪聲小數(shù)N分頻鎖相環(huán)的設(shè)計(jì)


















評(píng)論