一、重溫一下系統結構
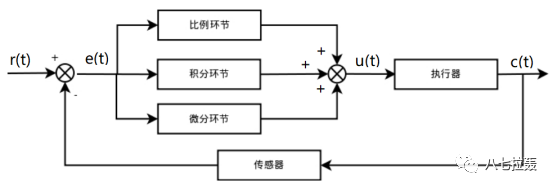
以爐溫控制系統為例,仔細觀察一下其原理圖及框圖。思考一下:哪些環節可以隨時更改或者說容易調整?
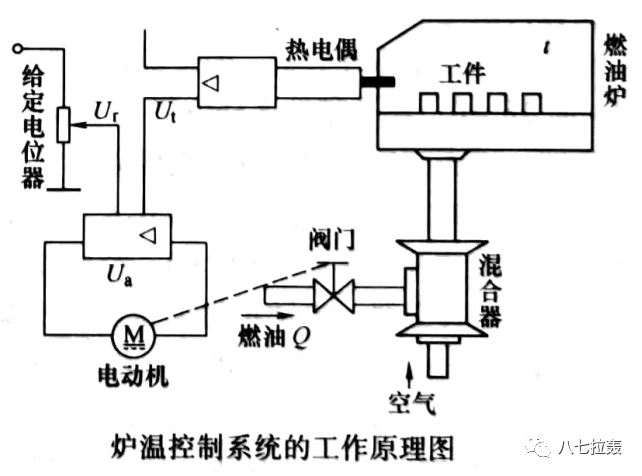
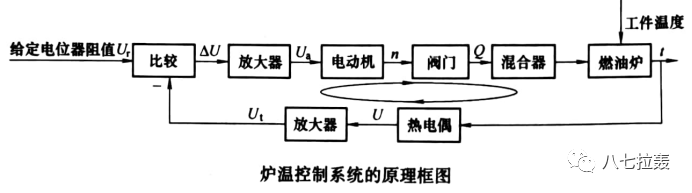
應該容易理解:對于一個已經搭建成型的系統,其中某些模塊或者環節基本上就難以再修改了,除非重建。例如上面這個爐溫控制系統,其中的燃油爐、混合器、已鋪設好的各個管路、閥門及驅動閥門的電機等,更換或者重建的成本是比較高的。
再換一個角度,對于一個控制工程師,不可能所有東西都是自己設計制作的,例如上面爐溫控制系統中,傳感器、電機、閥門、管道、混合器、燃油爐等基本都是在市場上選購的。這些模塊的特性是相對固定的,較難改動。
但是放大器電路(可能包含軟、硬件)是控制工程師設計的,那么是可以根據系統整體性能要求去調整改變的。我們一般把方便調節且能夠由此控制系統性能的部分稱為系統的控制器。
系統校正(即調整系統性能)如果需要增加裝置,一般是在控制器里實現的。
一般增加的校正裝置或環節,主要通過串聯或者反饋的方式接入系統。還有前饋或復合等方式。
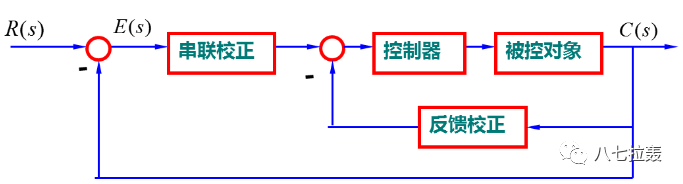
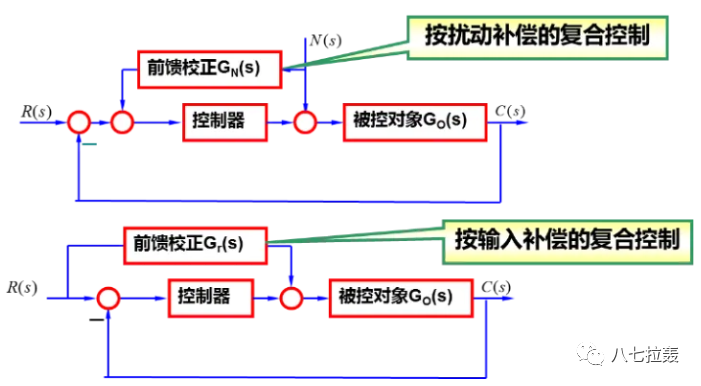
二、系統校正方法簡介
- 串聯“滯后、超前”校正裝置來改善系統性能
利用校正裝置改變原系統頻率特性曲線的形狀,使其具有合適的低中高頻特性,從而獲得滿意的穩態和暫態響應特性。
一般是根據性能指標要求,有針對性的選擇“滯后”、“超前”或“滯后——超前”裝置,再通過分析和計算求出校正裝置的參數。最后驗算或驗證設計結果,如不能滿足全部性能指標要求,需重新調整參數甚至結構,直至全部滿足。
該方法校正裝置結構簡單,容易實現。 如果希望校正后系統的穿越頻率明顯高于原系統的穿越頻率,一般采用“超前”校正,在新的穿越頻率處提供一定的相角超前量;如果希望校正后系統的穿越頻率明顯低于原系統的穿越頻率,一般采用“滯后”校正;如果希望校正后系統的穿越頻率與原系統接近,則采用“滯后——超前”,主要提供合適的相角超前量。 本方法需要充分了解原系統的頻率特性,對于大型或者復雜的系統,這是一件比較困難的事情。
- PID串聯校正
PID控制理念最早提出是在1932年,出生于瑞典后移民美國的物理學家哈利奈奎斯特(H Nyquist),在他的一篇論文當中提出了采用圖形的方法來判斷系統的穩定性。在他的基礎上,荷蘭裔科學家亨伯德(H W Bode)(“伯德圖/波特圖”創始人)等人建立了一整套在頻域范圍設計反饋放大器的方法,后被用于自動控制系統的分析和設計,這也是PID算法最早從書面走向實踐。與此同時,反饋控制原理開始應用于工業過程中。1936年英國的考倫德(A Callender)和斯蒂文森(A Stevenson)等人給出了 PID控制器的方法,自此PID算法正式形成了,并且后來在自動控制技術中占有非常重要的地位。
PID校正裝置是用比例(Proportional)、積分(Integral)和微分(Derivative)控制規律組成的串聯校正裝置,使用方便,適應性強,易于工程實現。而且根據需要,可以變形為P、PI或PID等類型調節器。目前在理論上已經證明,對于過程控制的典型對象——“一階滯后+純滯后”與“二階滯后+純滯后”的控制對象,PID控制器是一種最優控制。

在時域內,PID連續公式如下:
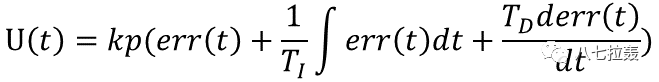
離散公式如下:
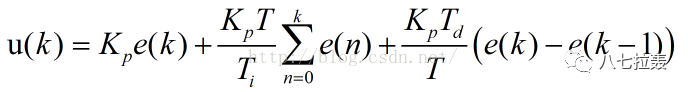
采用PID調節器,往往并不需要知道于控制對象的精確數學模型,這是它的優點,但也正因如此,其參數通常也都是根據經驗在線整定,以便得到滿意的控制效果 。隨著計算機技術的發展,PID控制算法已能用電腦或者嵌入式設備簡單實現,由于軟件系統的靈活性,PID算法可得到修正而更加完善。比如平衡小車,倒立擺,四軸飛行器,溫度調節都用到了PID,可以說一切控制系統都可以應用PID。
- 反饋校正
有時由于系統本身的特性,在局部反饋支路中添加校正裝置可能更有效,特別是針對有重大妨礙作用的某些環節。采用反饋控制,不僅能得到與串聯校正相同的效果,還能起到改善系統整體控制性能的特殊效果。
采用反饋校正后,系統對其所包圍的原系統各環節的特性參數變化不敏感,因此對這部分元件的要求可以降低,但對反饋環節中的元件要求較高。
三、如何理解P、I、D
- 首先理解控制——需要將某一個物理量“保持穩定”的場合,比如維持平衡、穩定溫度、轉速等,那么就需要控制這個物理量。
- 開關式控制
例一 :控制一個“熱得快”,讓一鍋水的溫度保持在50℃。控制策略——小于50度就打開加熱,大于50度就斷電。這就是開關式控制,方法很簡單,在要求不高的情況下,確實可以這么干。
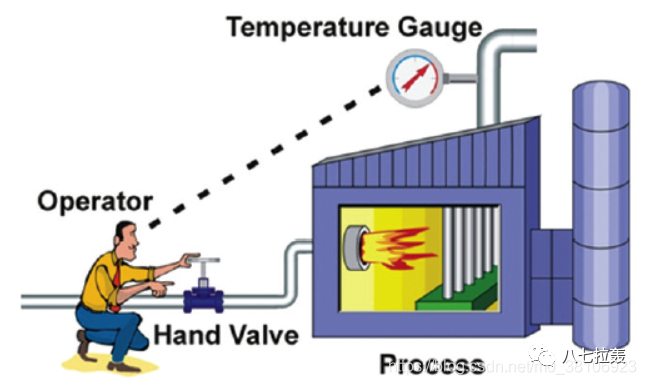
例二 :如果控制對象是一輛汽車,希望車速保持在50km/h不動。如果還是采用開關式控制策略,假如汽車的定速巡航電腦在某一時間測到車速是45km/h。它立刻命令發動機:加速!然后發動機那邊就100%全油門,嗡的一下,汽車急加速到了60km/h。這時電腦又發出命令:踩死剎車!很容易想象到,這樣的策略是肯定不行的。
如果考慮到實際器件均存在一定的延遲或慣性,那簡單粗暴的開關式控制甚至可能都不能讓系統穩定下來。
- PID控制
PID調節器各增益參數增加對系統時域指標的影響如下:

但是表中的關系并非絕對的,只是表示一定范圍內的相對關系,而且各參數之間還會相互影響,因此本表僅供定性輔助分析。下面對各參數的實際物理意義做一些探討。
①比例系數KP
P就是比例的意思。它的作用最明顯,原理也最簡單。當實際值比較接近目標時,P的控制作用就比較小。越接近目標,P的作用越溫柔。
例一 :控制水溫,將它現在的『當前溫度值』與我們期望的『目標溫度值』比較。當兩者差距不大時,就讓加熱器“輕輕地”加熱一下;要是因為某些原因,溫度降低了很多,就讓加熱器“稍稍用力”加熱一下;要是當前溫度比目標溫度低得多,就讓加熱器“開足馬力”加熱,盡快讓水溫到達目標附近,這便是P的作用。
也就是讓調節裝置的“調節力度”與偏差(目標值減去當前值)成比例關系,就可以實現最基本的“比例”控制了——KP越大,調節作用越激進,KP調小會讓調節作用更保守。
例二 :對于一個平衡車,僅有P的作用,你會發現,平衡車在平衡角度附近可能會出現來回“狂抖”的現象,比較難穩住。
例三: 控制目的是要保證某個水缸里的水位永遠的維持在1米的高度。假設初始時刻,水缸里的水位是0.2米,那么當前時刻的水位和目標水位之間是存在一個偏差error,且error為0.8。此時,假設旁邊站著一個人,通過人工往缸里加水的方式來控制水位。如果單純用比例控制算法,就是指加入的水量u和偏差error是成正比的,即u=KP*error。
假設KP取0.5,那么t=1時(表示第1次加水,也就是第一次對系統施加控制),那么u=0.5*0.8=0.4,所以這一次加入的水量會使水位在0.2的基礎上上升0.4,達到0.6。接著,t=2時刻(第2次施加控制),當前水位是0.6,所以error是0.4。u=0.5*0.4=0.2,會使水位再次上升0.2,達到0.8......如此這么循環下去,就是比例控制算法的運行方法。可以想到,最終水位會達到我們需要的1米。
但是,單單比例控制存在著一些不足,其中一點就是可能存在穩態誤差!
像上述水缸水位控制,根據KP取值不同,系統最后都會達到1米,只不過KP大了到達的快,KP小了到達的慢一些,看起來不會有穩態誤差。
但是,考慮另外一種情況,假設這個水缸在加水的過程中,存在漏水的情況!例如每次加水的過程,都會漏掉0.1米高度的水。仍設KP取0.5,那么會存在著某種情況,假設經過幾次加水,水缸中的水位到0.8時,水位將不會再變換!!!因為,水位為0.8,則誤差error=0.2. 所以每次往水缸中加水的量為u=0.5*0.2=0.1,同時,每次加水,缸里又會流出去0.1米的水!!!加入的水和漏水相抵消,水位將不再變化!!
也就是說,我的目標是1米,但是最后系統達到0.8米的水位就不再變化了,且系統已經達到穩定。由此產生的誤差就是穩態誤差了。
在實際情況中,這種類似水缸漏水的情況往往更加常見,比如控制汽車運動,摩擦阻力就相當于是“漏水”,控制機械臂、無人機的飛行,各類阻力和消耗都可以理解為本例中的“漏水”。
所以,單獨的比例控制,在很多時候并不能滿足要求。
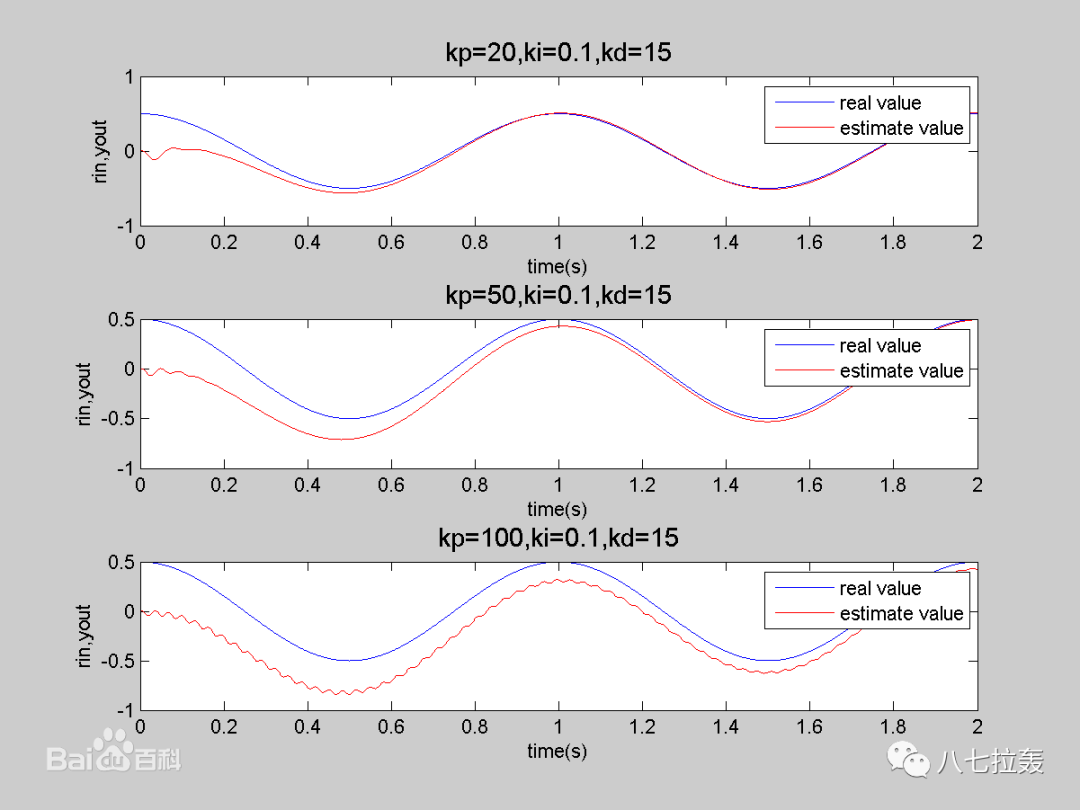
改變比例作用的效果
②微分系數KD
微分D的作用更好理解一些,所以先說D,最后再說I。
不難發現,僅有P的作用,水溫控制得上上下下,而平衡車甚至都不能穩定站起來,整個系統不是特別穩定,總是在“抖動”。
例一: 我們思考一個彈簧:在平衡位置上拉它一下,然后松手,這時它會震蕩起來。如果阻力很小,它可能會震蕩很長時間,才會重新停在平衡位置。但如果把彈簧系統浸沒在水里,同樣拉它一下,此時,重新停在平衡位置的時間就短得多。因此我們需要一個控制作用——類似于“阻尼”的作用,讓被控制的物理量的“變化速度”盡快趨于0。
而D的作用就是讓物理量的速度趨于0,無論什么時候,只要這個量具有了速度,D就向相反的方向作用,剎住這個變化。微分系數KD越大,向速度相反方向剎車的力道就越強。
例二: 考慮剎車情況。平穩的駕駛車輛,當發現前面有紅燈時,為了使得行車平穩,基本上提前幾十米就放松油門并踩剎車了。當車輛離停車線非常近的時候,則使勁踩剎車,使車輛停下來。整個過程可以看做一個加入微分的控制策略。
微分,在離散情況下,就是error的差值,也就是t時刻和t-1時刻error的差,即u=KD*(error(t)-error(t-1)),其中的KD是一個系數項。
可以看到,在剎車過程中,因為error是越來越小的,所以這個微分控制項一定是負數,在控制中加入一個負數項,他存在的作用就是為了防止汽車由于剎車不及時而闖過了線。從常識上可以理解,越是靠近停車線,越是應該注意踩剎車,不能讓車過線,所以這個微分項的作用,就可以理解為剎車,當車離停車線很近并且車速還很快時,這個微分項的絕對值(實際上是一個負數)就會很大,從而表示應該用力踩剎車才能讓車停下來。
**例三:**對于水缸加水的例子,就是當發現水缸里的水快要接近1的時候,加入微分項,可以防止給水缸里的水加到超過1米的高度,說白了就是減少控制過程中的震蕩。
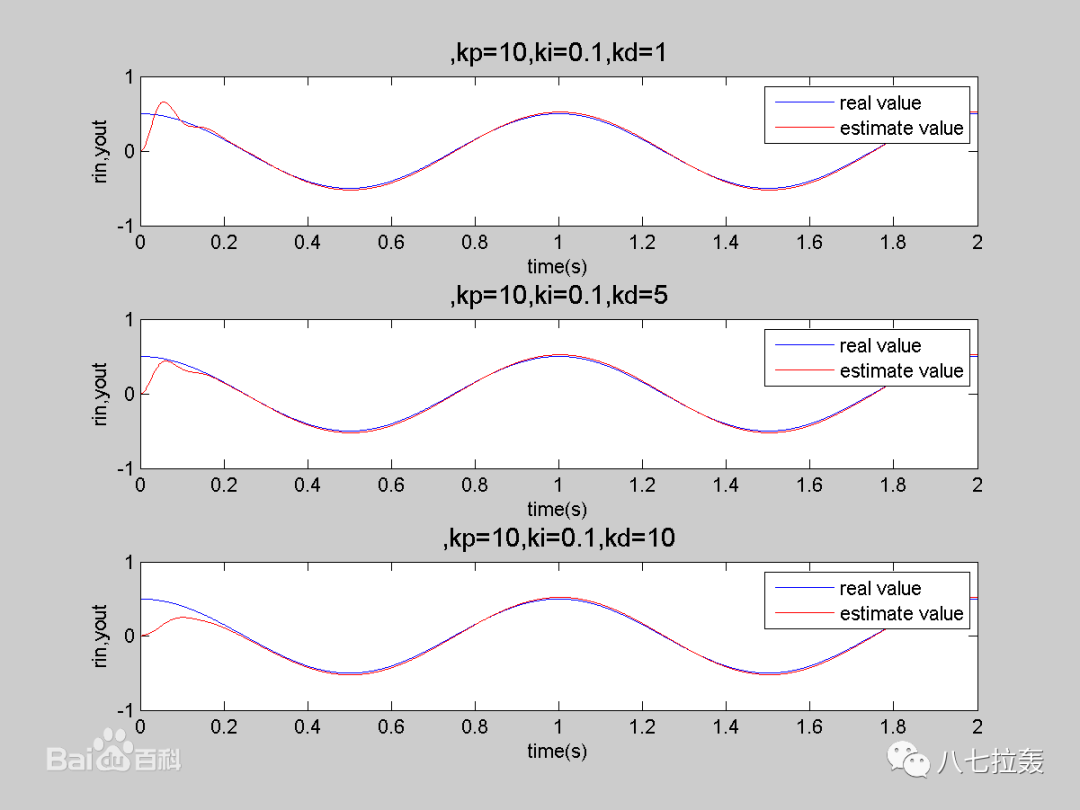
改變微分作用的效果
③積分系數KI
看起來P、D就可以讓物理量保持穩定,那為什么還要I呢?
因為我們忽視了一種重要的情況!
例一: 還是以熱水為例,假如有個人把加熱裝置帶到了一個非常冷的地方,水需要燒到50℃。
在P的作用下,水溫慢慢升高。直到升高到45℃時,他發現了一個不好的事情:天氣太冷,導致此時出現了,水散熱的速度和P控制的加熱速度相等了。
這可怎么辦?
P兄這樣想:我和目標已經很近了,只需要輕輕加熱就可以了。D兄這樣想:加熱和散熱相等,溫度沒有波動,我好像不用調整什么。
于是,水溫永遠地停留在45℃,永遠到不了50℃。
根據常識我們知道,應該進一步增加加熱的功率。可是增加多少該如何計算呢?
這時候就可以設置一個積分量,只要偏差存在,就不斷地對偏差進行積分(累加),并反應在調節力度上。
如此一來,即使45℃和50℃相差不太大,但是隨著時間的推移,只要沒達到目標溫度,這個積分量就不斷增加。系統就會慢慢意識到:還沒有到達目標溫度,該增加功率啦!
到了目標溫度后,假設溫度沒有波動,積分值就不會再變動。這時,加熱功率仍然等于散熱功率。但是,溫度是穩穩的50℃。
例二: 控制水缸水位,如果僅僅用比例,可以發現存在穩態誤差,最后的水位就卡在0.8了。于是,在控制中,我們再引入一個分量,該分量和誤差的積分是正比關系。所以,比例+積分控制算法為:u=KP*error+ KI?∫ error 。
還是假設第一次的誤差error是0.8,第二次的誤差是0.4,至此,誤差的積分(離散情況下積分就是累加),∫error=0.8+0.4=1.2, 這個時候的控制量,除了比例的那一部分,還有一部分就是一個系數 KI乘以這個積分項。由于這個積分項會將前面若干次的誤差進行累計,所以可以很好的消除穩態誤差(假設在僅有比例項的情況下,系統卡在穩態誤差了,即上例中的0.8,由于加入了積分項的存在,會讓輸入增大,從而使得水缸的水位可以大于0.8,漸漸到達目標的1.0)這就是積分項的作用。
積分系數KI的值越大,即積分時的乘數就越大,則積分效果越明顯。
所以I的作用就是,減小穩態情況下的誤差,讓受控物理量盡可能接近目標值。
I在使用時還有個問題:如果在剛開始加熱時,積分量就積得太大,則難以控制系統穩定。因此需要設定積分限制,防止系統不穩。
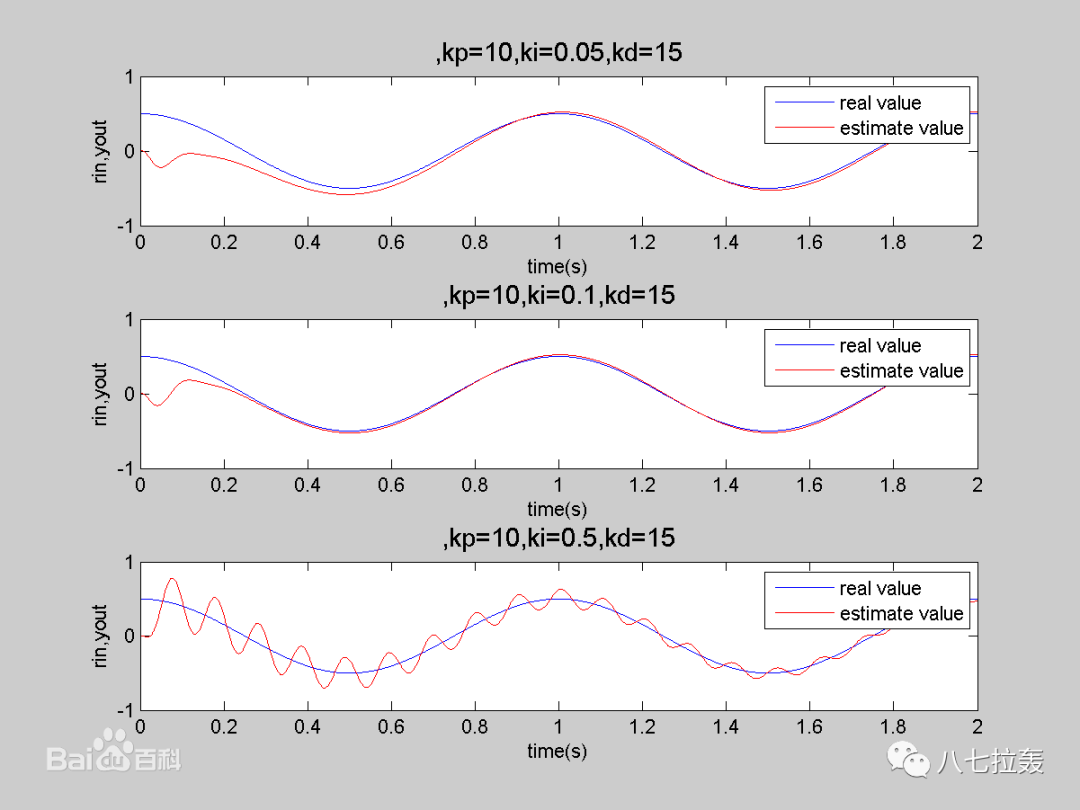
改變積分作用的效果
后記:也有網友這么理解PID——p是控制現在,i是糾正曾經,d是管控未來!
也有網友認為, P對應“快”,對誤差進行預判、做出快速反應 ;I對應“準”,消除穩態誤差; D對應“穩”,即穩定性,抑制快速變化 。
可以發現不同物理系統,三個參數的物理意義有相同之處,也有所不同。尤其是位置式PID控制和增量式PID控制算法對應的物理意義有較大區別。
-
傳感器
+關注
關注
2560文章
52165瀏覽量
761480 -
控制系統
+關注
關注
41文章
6739瀏覽量
111596 -
PID控制
+關注
關注
10文章
461瀏覽量
40861 -
調節器
+關注
關注
5文章
870瀏覽量
47099 -
反饋放大器
+關注
關注
0文章
38瀏覽量
8013
發布評論請先 登錄
相關推薦
一種基于路測數據的傳播模型校正方法
請問adxrs646溫度校正的多點校正方法是什么?
光譜儀的正確校正方法
基于微機處理的熱電偶動態誤差校正方法的研究
傳感器非線性的硬件校正方法
基于圖像分析的偏色檢測及顏色校正方法
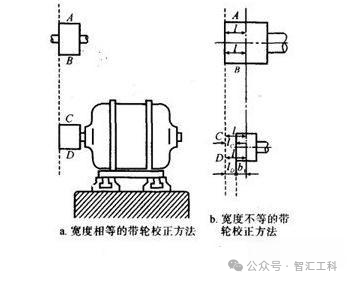
電動機傳動裝置的安裝和校正方法


















評論