一、交流純電阻電路

1、電壓和電流的關系

含有白熾燈、電爐、電烙鐵、變阻器等負載的電路，其電感和電容可略去不計，在實用上可看作純電阻電路。在純電阻元件中，流過的正弦電流與電壓同頻率、同相位，其瞬時值等于相應電壓瞬時值除以電阻，即電壓和電流的瞬時值關系服從歐姆定律，最大值、有效值也遵循歐姆定律。

2、功率計算

交流純電阻電路的功率計算如下:

電阻消耗的功率在任一瞬時都是正值，即在任一時刻都向電源吸取電能，一周期內瞬時功率的平均值稱為平均功率，又稱有功功率，用P表示，單位為 w，它等于電壓有效值和電流有效值的乘積，即

P=UI=I2R=U2/R

二、交流純電感電路

1、電壓和電流的關系

由電感作負載所組成的電路稱為純電感電路。在純電感電路中，自感電動勢是唯一影響電流變化的因素，且線圈的外加電壓和自感電動勢必是大小相等、方向相反、互相平衡。由楞次定律可知，自感電動勢的方向總是阻礙電流的變化，電流i較自感電動勢eL超前90°，即電路的電壓與電流同頻率時，電流相位滯后電壓相位90°。
2、感抗
計算交流電路時，常用感抗XL來表示自感電動勢所產生的阻力，即電感線圈對交變電流的阻礙作用，其大小與交流電的頻率和線圈本身的電感成正比，即

XL=ωL=2πfL

式中 XL--感抗，Ω；

f--頻率，Hz；

L--線圈電感，H。

3、感性無功功率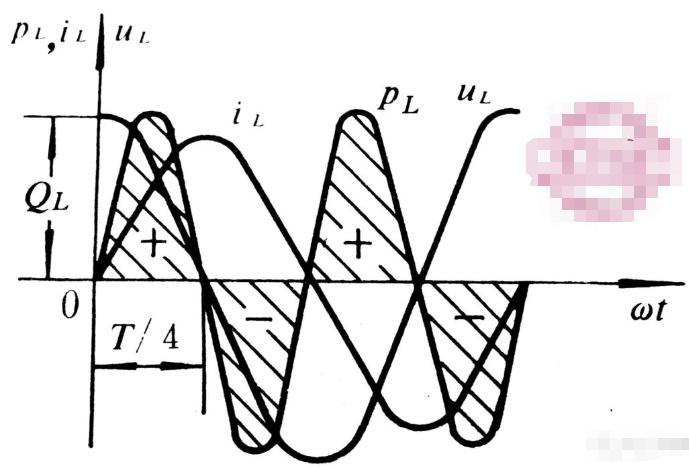

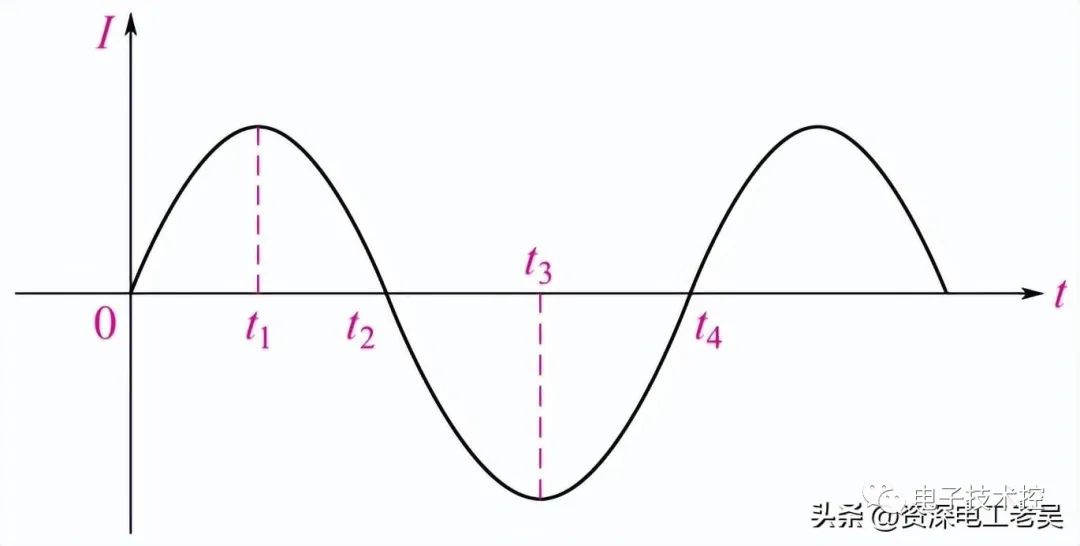
1）如上圖所示功率曲線，瞬時功率以電壓或電流頻率的二倍關系按正弦規律變化。在0π/2 段的瞬時功率是正值，表示線圈從電源吸取能量轉換為磁場能，在π/2π段的瞬時功率是負值，表示線圈將磁場能轉化為電能而送還電源，以此循環往復。由此可知：電感電路中的平均功率等于零，說明該電路不消耗有功功率，只有線圈與電源之間的能量相互轉換，故電感線圈是儲能元件。

2）為了定量地分析電感線圈與電源之間能量交換的情況，將瞬時功率的最大值稱為感性無功功率，用字母QL表示。其單位符號為var或kvar。

3）電力系統中常用無功功率來表示電源向電感性負載所提供的磁場能量的大小。“無功”決不能理解為“無用”，它是具有電感的設備正常工作的必要條件。

三、交流純電容電路

1、電壓和電流的關系
1）將電容器接在交流電源上組成的電路，并略去電路中的一切電阻和電感，叫做純電容電路。
2）電容器是兩個彼此絕緣又互相靠近的導體，是儲存電能的元件。在交流電壓的作用下，隨著電壓的不斷交變，在電容元件中不斷地進行充電和放電，電路中就會有持續的交流電流通過。
3）當電源電壓為正值時，電容器被充電，電路中有充電電流；當電源電壓下降時，電容器向電路放電，電路中有放電電流；在交流純電容電路中，電流i與電荷的變動速率(dQ/dt)或與電容兩端電壓的變動速度(C·du/dt)成正比。當正弦電壓是零值時，它的變動速率最大，因而此時電流具有極大值；反之，當電壓是最大值時，它的變動速率等于零，因此這時電流值等于零。
純電容電路中，電容電流為

i=Cdu/dt=CUm?dsinωt/dt

=ωCUmcosωt=Imsin(ωt+π/2）

從式中明顯看出在純電容電路中， 電流在相位上超前電壓π/2弧度(90°)，且Im=ωCUm。

2、容抗

在純電容電路中，電容周期性地被電源充電和對電路放電，故電容器兩極上建立的電壓極性與電源電壓極性總是相同的，因此電容器極板上的電壓相當于反電勢，對交流電流具有阻礙作用，這種礙流作用稱為電容容抗(簡稱容抗)，用符號Xc表示。其電流比外施電壓超前π/2相角，且同頻率。

電容器的容抗Xc與交流電的頻率和電容器本身的電容量C成反比，即

Xc=1/2πfC=1/ωC

式中Xc--容抗，Ω；

f--頻率，Hz；

C--電容量，F。

3、容性無功功率

從上圖所示的功率曲線可以看出：瞬時功率以電壓或電流頻率的二倍關系按正弦規律變化。充電時，從電源吸取能量并儲存在電容元件的電場中；放電時，把儲存在電場中的能量又送還給電源，進行著可逆的能量轉換而不消耗功率，所以平均功率為零。

為了衡量電源與電容電路間能量交換的情況，將瞬時功率的最大值稱為容性無功功率，用字母Qc表示，單位為var或kvar。

四、電阻與電感串聯電路

1、電壓和電流的關系

由于通過R、L的是同一電流，所以選電流作為參考向量，并設

i=Imsinωt

而電阻和電感上的電壓則分別為

uR=UmRsinωt

uL=UmLsin(ωt+90°)

根據基爾霍夫第二定律，電路方程式為u=uR+uL

其中Ur(=IR)與I同相，UL(=IXL)超前I90°。

根據上圖所示的電壓三角形可求得I與U 的量值關系和相位關系。

I與U的量值關系為

U=√U2R+U2L=√(IR)2+(IXL)2

=I√R2+X2L

I與U 的相位關系為

在RL電路中，I滯后U的相位角為φ。

2、阻抗

阻抗是電路中電阻與電抗的總和，在R、L串聯電路中，電路的阻抗Z為

Z=√R2+X2L，可得U=IZ或I=U/Z

阻抗Z的單位是Ω，代表 R、L串聯電路對交流電流的阻力。

根據上圖所示的阻抗三角形，在R、L串聯電路中，如已知R與L(ωL=XL)，可求出U與I的相位關系。

3、R、L電路中的功率

1）有功功率

也就是電路取用的功率，實際上是電阻所消耗的有功功率，其值為

P=URI=I2R

2）無功功率

是電路中電感與電源進行能量交換的部分，其值為

QL=ULI=I2XL

3）視在功率

電路中總電壓有效值U和電流有效值I的乘積稱為視在功率，用以表征電源所能輸出的最大有功功率的數值。視在功率用S表示。S=UI

式中U--單位為V；

I--單位為A；

S--單位為VA(伏安)，常用單位kVA。

4、功率因數

根據上圖所示的功率三角形，可求得：

P=URI=UIcosφ=Scosφ

Q=ULI=UIsingφ=Ssingφ

S=√P2+Q2

cosφ=P/S，cosφ稱為功率因數，φ稱為功率因數角(又稱阻抗角，實際上就是U與I間的相位角)。

五、電阻、電感與電容串聯電路

電阻、電感與電容串聯的交流電路如下圖所示：

1、電壓和電流的關系

由于通過 R、L、C的是同一電流，所以選電流I作參考向量。

i=Imsinωt

電阻、電感和電容上的電壓分別為

uR=UmRsinωt

uL=Umsin(ωt+90°)

uc=Umsin(ωt-90°)

根據基爾霍夫第二定律，可列出 R、L、C 串聯電路的方程式為

u=uR+uL+uc

用向量方程式表示時為

U=UR+UL+Uc

其中UR=IR，UL=IXL，Uc=IXc，其向量圖可根據i、ux、UL、Uc方程式中的初相和各量的有效值畫出，如上圖(b)所示。根據向量圖可求得U、I的大小與兩者間的相位角：

U=√U2R+(UL-Uc)2=I√R2+(XL-Xc)2

I=U/√R2+(XL-Ⅹc)2

I與U 間的相位角為φ。

2、阻抗與電抗

阻抗Z=√R2+(ⅩL-Xc)2

式中的XL-Xc=X，稱為電抗，單位為 Ω。

當XL>Xc時，電路呈感性，φ為正值，表示電流滯后電壓一個φ角。

當Xc>XL時，電路呈容性，φ為負值，表示電流超前電壓一個φ角。

不論XL>Xc 還是XL

3、R、L、C 串聯電路中的功率

有功功率 P=URI=I2R；

電感的無功功率 QL=ULI=I2XL；

電容的無功功率Qc=UcI=I2Xc；

電路總的無功功率 Q=QL-Qc。QL>Qc時，電路呈感性；QL

視在功率 S=√P2+(QL-Qc)2

4、功率因數

電路的功率因數cosφ=P/S，當XL>Xc或QL>Qc時的功率因數稱滯后的功率因數；當XL

** 六、R、L串聯后與C并聯電路**
下圖為R、L 串聯后與C并聯的電路。

1、電壓和電流的關系

由于R、L支路與C支路處于同一電壓之下，所以選電壓的向量作為參考，即 u=Umsinωt
R、L 串聯電路的電流

I1=U/Z1=U/√R2+X2L
C支路是電容電路，電流Ic超前電壓U90°。電流 Ic=U/Xc
根據基爾霍夫第一定律，i=Ic+I1。

利用以上各關系式，可作出如上圖(b)的向量圖。
當I1sinφ1>Ic時，φ為正值，電路總電流滯后于電壓一個φ角，電路呈感性狀態；當I1sinφ12、功率
上圖中R、L 支路的各項功率為
P1=I21R；QL=I21XL；S1=UI1。

C支路的各項功率為
Pc=0；Qc=I2cXc；Sc=UIc

所以電路各項的總功率為
P=P1+Pc=P1。電路中總有功功率為各分支電路中的有功功率的算術和，即P=P1+P2+P3+...=∑Pn；

Q=QL-Qc。電路中總無功功率為各分支電路中的無功功率的代數和，感性為正，容性為負，即Q=Q1士Q2士Q3士...=∑Qn；

S=√(∑Pn)2+(∑Qn)2。電路中總視在功率為總有功功率和總無功功率的幾何和。總視在功率 S≠S1+S2+...Sn，這點必需牢記。

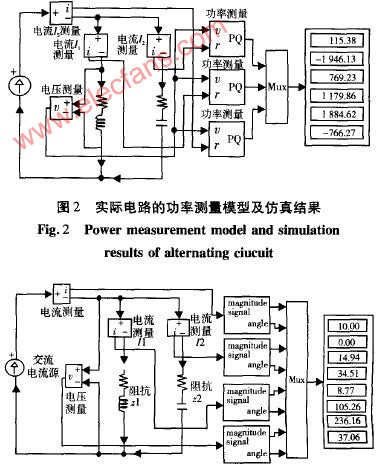
圖2(a)電路的各項總功率也可利用圖1(b)直接求得:

總有功功率P=UIcosφ

總無功功率Q=UIsinφ

總視在功率S=UI