當我們觀賞精美的電影畫面的游戲場景,或者在虛擬現實世界中暢游時,有一個關鍵角色一直默默發揮著作用,那就是GPU(圖形處理器)。你是否曾好奇過,為什么GPU在圖像渲染過程中會選擇以三角形作為基本元素呢?
簡單的數學屬性
三角形之所以成為計算機圖形學中的“明星”,部分原因在于其簡單的數學屬性。在計算機圖形學中,我們使用向量和矩陣來表示和變換圖形對象。對于三角形,只需要定義三個頂點的坐標,然后通過簡單的向量運算,就可以輕松地計算出其邊長、角度、面積等屬性。這些屬性對于實現光照、陰影和紋理等效果至關重要。
三角剖分
現實世界中的物體形狀各異,從彎曲的樹葉到銳利的建筑輪廓。然而GPU無法直接處理這么多種形狀,這時三角形的優勢就顯現出來了。通過一種稱為“三角剖分”的技術,將復雜的多邊形或曲面劃分為許多小的三角形。這種分解的原理基于以下幾個主要思想:
01、三角形的簡單性:
三角形是計算機圖形學中最簡單的多邊形之一,具有簡單的數學計算和屬性定義。通過將復雜的形狀分解為小三角形,可以將復雜的計算和處理任務分解為一系列簡單的計算步驟。
02、逼近和光滑性:
多邊形和曲面可能具有復雜的幾何形狀,但是由于三角形具有逼近性,通過合理的三角剖分可以很好地逼近復雜形狀。在每個小三角形內部可以進行插值計算,從而實現光滑的漸變效果,提高渲染質量。
03、圖形處理的高效性:
計算機圖形學中很多技術和算法都是基于三角形的,如光柵化、像素填充、著色和紋理映射等。通過使用三角形作為基本元素,這些算法可以更加高效地運行,從而加速圖像處理和渲染過程。三角剖分的過程通常涉及以下幾個步驟:
- 頂點選擇:首先,從多邊形的頂點集合中選擇三個頂點作為一個初始三角形。這些頂點可以是多邊形的頂點或者是通過插值計算得到的頂點。
- 邊選擇:選擇一個邊,將多邊形分割成兩個子多邊形。選擇邊的方法可以根據不同的三角剖分算法來確定,常見的方法有“最遠點法”和“Delaunay三角剖分”。
- 頂點插入:將新的頂點插入到邊的中點,從而生成兩個新的三角形。這個過程通常會涉及到頂點的插值和屬性計算。
- 遞歸或循環:重復上述步驟,直到不再有可分割的邊。這可能需要進行遞歸或者迭代的過程,直到整個多邊形被分解為一系列小三角形。
通過這種方式,三角剖分可以將復雜的形狀分解為一系列簡單的小三角形,從而使得圖像處理和渲染更加高效和精確。這種技術在計算機圖形學中被廣泛應用于各種領域,為圖像處理提供了強大的支持。因此,GPU可以更好地處理和逼近各種物體。
掃描線算法
將圖像渲染到屏幕上,一種常用的方法是掃描線算法。這種算法將圖像分為一系列水平的掃描線,然后在每條掃描線上填充相應的顏色。三角形的邊界與掃描線的相交非常容易,因此,在掃描線算法中使用三角形能夠使渲染過程更加高效。這種算法的有效性也在一定程度上推動了GPU選擇三角形作為基本元素的趨勢。
正是因為這些屬性,GPU選擇了以三角形作為其圖像渲染的基本元素。從簡單高效的數學計算到圖形硬件的優化設計,從多邊形逼近到掃描線算法的運用,三角形在計算機圖形學中發揮著不可替代的作用。正是這種基本元素的選擇,為我們呈現出了一個個令人嘆為觀止的視覺世界。
-
處理器
+關注
關注
68文章
19349瀏覽量
230278 -
gpu
+關注
關注
28文章
4753瀏覽量
129067 -
圖形處理
+關注
關注
0文章
45瀏覽量
13798
發布評論請先 登錄
相關推薦
【「算力芯片 | 高性能 CPU/GPU/NPU 微架構分析」閱讀體驗】--了解算力芯片GPU
淺談電動機三角接法是什么意思?舉例分析
三相電機三角形連接有哪些參數關系?
三相交流電動機星形與三角形接線方法主要區別在哪?
什么是三相電機三角形接法?定義是什么?
三角波發生器的組成和應用
三角形連接和星形連接的基本概念和特點
三角形連接線電流和相電流的關系
高壓電容器可以同時采用星形及三角形接法嗎

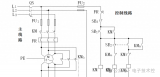
電動機星形/三角降壓啟動電路圖接線原理
華為Pura 70手機后置攝像頭采用三角形島式設計
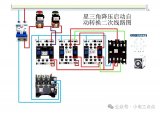
星三角降壓啟動自動轉換二次線路圖




 解密GPU圖像渲染:為什么選擇三角形作為基本元素?
解密GPU圖像渲染:為什么選擇三角形作為基本元素?










評論