米勒頻率補償（Miller frequency compensation）使得可以使用相當小的補償電容Cf值。這是非常需要的，不僅因為C?可以在片上制造，而且因為它導致比例如并聯電容補償更快的動態。這是因為壓擺率（slew rate,），開環帶寬和全功率帶寬與C f成反比。

現在，就C?的大小而言，對閉環增益的補償一直到單位增益是最保守的。有許多應用涉及閉環增益大于最小值，例如大于Amin = 10 V / V，這將適用于更小的C?，從而享受更快的動態。

讓我們使用我們運行的PSpice電路示例，首先在我的運放頻率補償文章中介紹的，來比較去補償（decompensation）與完全補償：

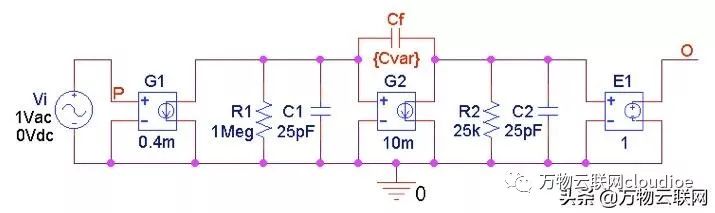
圖1

圖1. PSpice電路繪制完全補償和去補償（decompensation）的開環增益。

PSpice的結果如下圖所示：

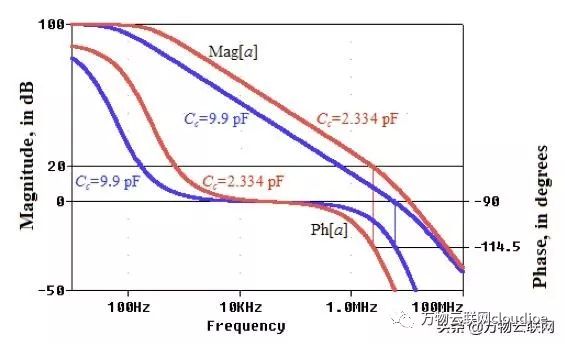
圖2

圖2.具有完全補償的開環增益（對于閉環增益≥0dB，C?= 9.90 pF）和去補償（decompensation）（對于閉環增益≥20dB，C?= 2.334 pF）。兩種補償均享受φm≥65.5°

結果引出以下觀察：

在完全補償（C?= 9.90 pF）的情況下，0 dB增益的交叉頻率?x≈5.86MHz，相位裕度φm= 65.5°。此外，如果我們將全補償運算放大器配置為20 dB閉環增益，則它具有?x≈633kHz和φm≈87°，甚至比0 dB增益更大。

通過去補償（decompensation）（C?= 2.334 pF），20 dB增益具有?x≈2.37MHz（帶寬比完全補償更寬），并且仍然是φm= 65.5°。但是，如果我們將去補償（decompensation）運算放大器配置為0 dB閉環增益，它將具有?x≈11.1MHz和φm≈24°，這是一個很差的余量，因為去補償（decompensation）的器件意味著增益≥20dB。當φm≈24°時，20-dB增益將呈現約7％的峰值，并且瞬態響應具有約50％的過沖，這兩者通常都是不可接受的。

現在讓我們繼續考慮如何利用外部因素在電路中實現補償;例如，電阻器。

使用電阻器進行外部補償

盡管失代償運算放大器的閉環增益高于Amin（在上例中為Amin = 20 dB），但它們的優越動態性使其對于增益低于Amin的應用也具有吸引力。

但這會降低相位裕度φm，因此用戶有責任在外部補償電路，以便將φm保持在所需的水平。

為了說明，讓我們將圖1的運算放大器用于C?= 2.334 pF的失代償形式，讓我們將其配置為電壓跟隨器操作，如圖3（a）所示。

圖3

圖3.電壓跟隨器：（a）去補償（decompensation），（b）外部補償φm≈65.5°。

如上所述，該電路的相位裕度僅為φm≈24°。我們如何將其提高到φm= 65.5°？一個簡單的解決方案是將其1 /β曲線提高到20 dB，同時仍然確保單位增益。我們通過以1比9的比例連接電阻對Rc-Rf來實現這一點，如圖3（b）所示。理想化極限a→∞的閉環增益仍然存在：

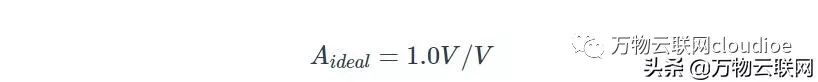
方程1

（這種情況是因為對于a→∞，運算放大器輸入端的電壓趨于零。這意味著通過Rc的電流為零，因此通過Rf也是零電流。因此，R?兩端的電壓為零，所以我們有Vo = Vi。）

然而，我們通過圖4（a）的測試電路找到的反饋因子β是：

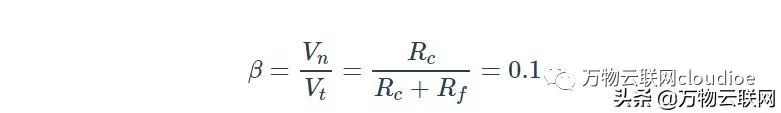
或1 /β= 10 = 20 dB（注意本例中1 /β≠Aideal）。

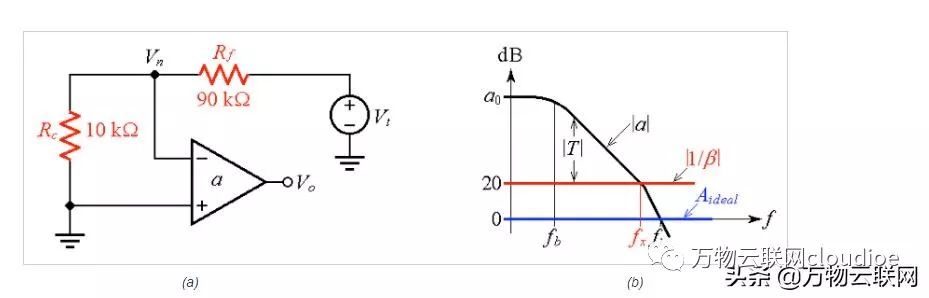
圖4

圖4.（a）找到圖3（b）的電壓跟隨器的反饋系數β的電路，以及（b）Bode-plot可視化的電路。

響應如圖5所示。

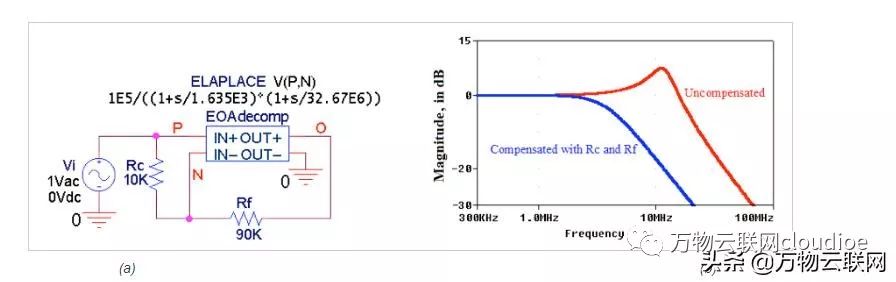
圖5

圖5.（a）PSpice電路可視化（b）圖3的電壓跟隨器的響應。拉普拉斯模塊模擬圖2的去補償（decompensation）響應，用C = 2.334pF獲得。

類似的推理線適用于圖6（a）的單位增益反相放大器。

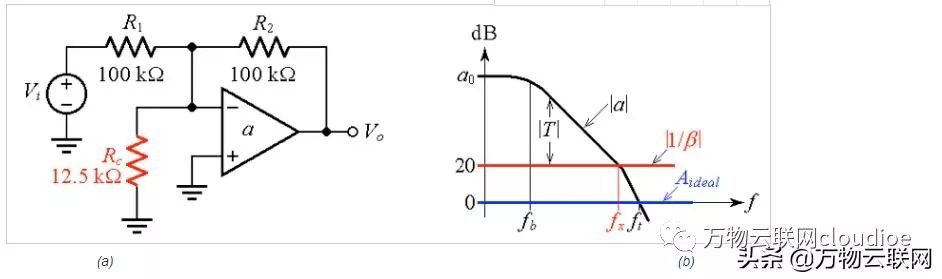
圖6

圖6.單位增益反相放大器的外部補償。

在這種情況下，在極限a→∞，我們有：

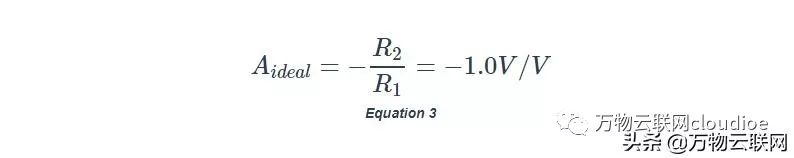
方程3

通過觀察，現在反饋因子變為：

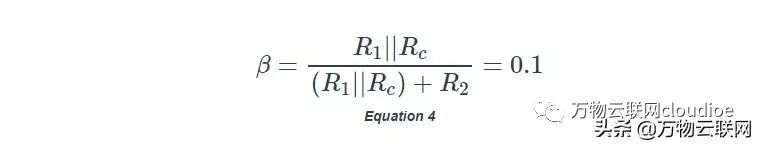
方程4

在這種情況下，選擇Rc以使（R1 || Rc）= R2 / 9。

電阻補償的應用（和缺點）

專門針對單位增益同相和反相放大器的上述討論可以很容易地推廣到除了單位閉環增益之外的情況，但仍然是1 <（1 + R2 / R1）

該電路是用作同相放大器（Aideal = 1 + R2 / R1）還是作為反相放大器（Aideal = -R2 / R1），只要條件（1 + R2 / R1）

電阻補償雖然簡單，但有兩個缺點：

a、任何可以用與非反相輸入串聯的電壓源建模的噪聲，例如輸入失調電壓VOS，都會被放大1 /β，因此也被稱為噪聲增益。

b、環路增益T =（圖4（a）中的aβ= -Vo / Vt）減小（在本示例中為10倍），導致電路的閉環DC精度下降。

輸入滯后補償

我們可以通過將合適的電容Cc與Rc串聯來減輕電阻補償的限制，如圖7（a）所示，用于反相放大器。

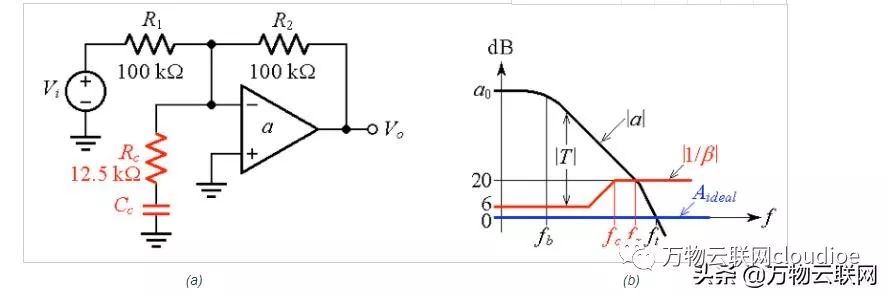
圖7

圖7.（a）單位增益反相放大器的輸入滯后補償，以及（b）波德圖可視化。

注意，為了確保所需的相位裕量，我們需要僅在交叉頻率?x附近欺騙放大器進入所需的閉合速率（ROC），而不是一直到DC。

物理上，1 /β曲線在電容阻抗幅度等于Rc的頻率?c處斷開，或| 1 /（j2πCc| = Rc，給定：

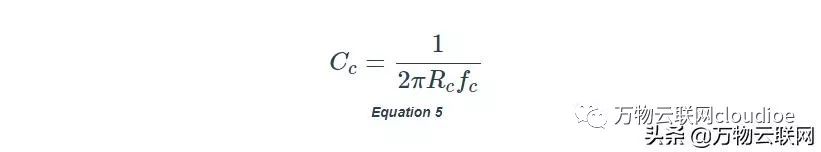
方程5

為了防止相位裕度φm的明顯侵蝕，通常將?c放置在低于?x的十倍左右，或者：

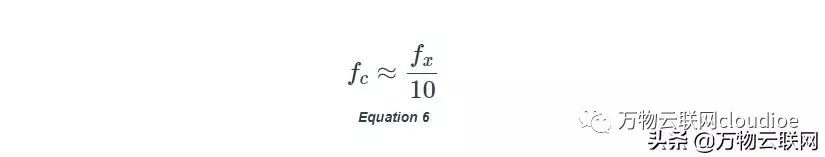
對于圖7（a）的電路，這意味著Cc≈54pF。圖8的模擬產生測量值?x= 2.38MHz和φm= 61°。

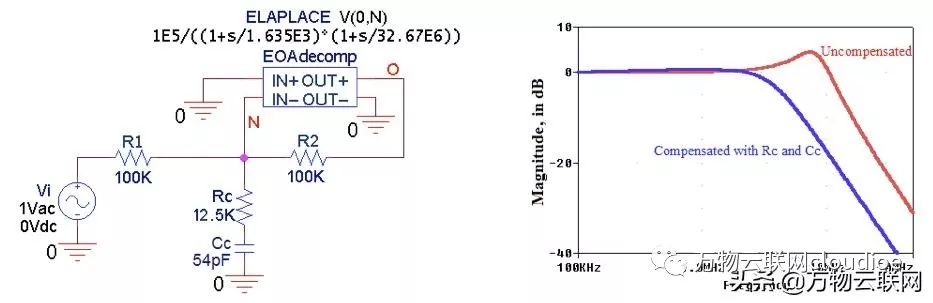
圖8

圖8.（a）PSpice電路到（b）可視化單位增益反相放大器的輸入滯后補償的穩定效應。

外頻補償的另一種方法

輸入滯后補償因在閉環響應中產生零極點雙重而臭名昭著，這導致了不可忍受的長建立時間特性。Michael Steffes提出的替代補償方法避免了這些缺點，如圖9所示。

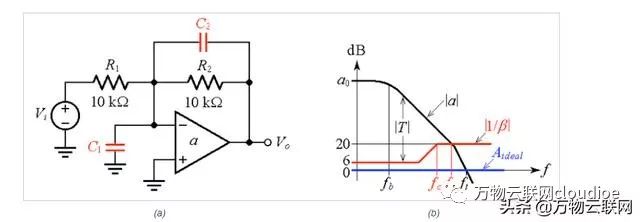
圖9

圖9.（a）Michael Steffes對去補償（decompensation）運算放大器的補償技術，以及（b）波德圖可視化。

我們在先前關于雜散輸入電容補償的文章中已經遇到過這種類型的電路，因此在那里做出的許多考慮也適用于本電路，唯一的區別是現在C1是有意的。

我們有興趣開發兩個條件來指定C1和C2的值。在高頻時，阻抗C1和C2的幅度比R1和R2小得多，我們可以忽略R1和R2，并說明在高頻時我們有1 /β→1 + C1 / C2。

施加1 + C1 / C2 = 20 dB = 10給出了我們電路示例的第一個條件：

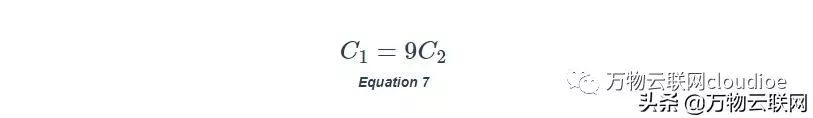
第二個條件源于這樣的事實：

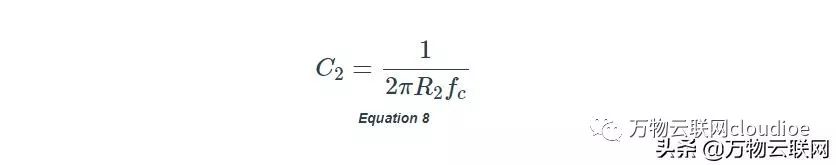
所以C2的值取決于我們決定定位?c的位置。

我們采用啟發式方法，而不是應用Steffes的詳細分析，因為這超出了本文的范圍。

我們從等式（6）和（8）開始，并使用圖10的PSpice電路觀察AC響應，因為我們通過減少C2逐漸增加?c，同時保持等式（7）的條件。

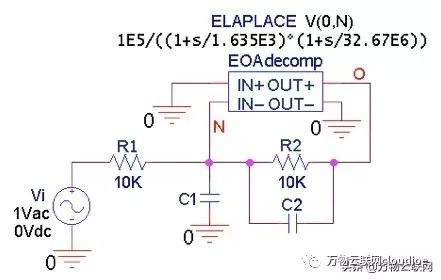
圖10

圖10.用于繪制圖9a的反相放大器的AC響應的PSpice電路。要繪制瞬態響應，請將AC輸入源更改為脈沖源。

當AC響應剛開始顯示峰值時，我們停止。該方法給出C2 = 12pF和C1 = 9C2 = 108pF，導致圖11的良好響應.AC響應具有2.36MHz的-3dB頻率。

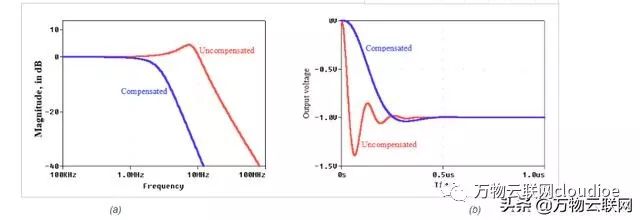
圖11

圖11.（a）AC響應和（b）圖10的反相放大器的階躍響應。

值得指出的是，通過將C1的值改變為9C2-Cn，可以將存在于反相輸入端的任何雜散電容Cn并入該補償方案中。因此，如果Cn = 20 pF，那么我們使用C1 = 88 pF。

在本文中，我們研究了去補償（decompensation）和外部補償的運算放大器。我們使用示例電路來演示可以通過各種方式實現運放頻率補償，并考慮每種方法的優缺點。