增加了濾波器的同相配置

上圖的運放在簡單的同相接法的基礎(chǔ)上增加了Cf濾波器，我們都知道電容器具有“ 通交流 ”的特性，但是交流信號的頻率有高有低，多大的頻率才能“通過”電容器呢？

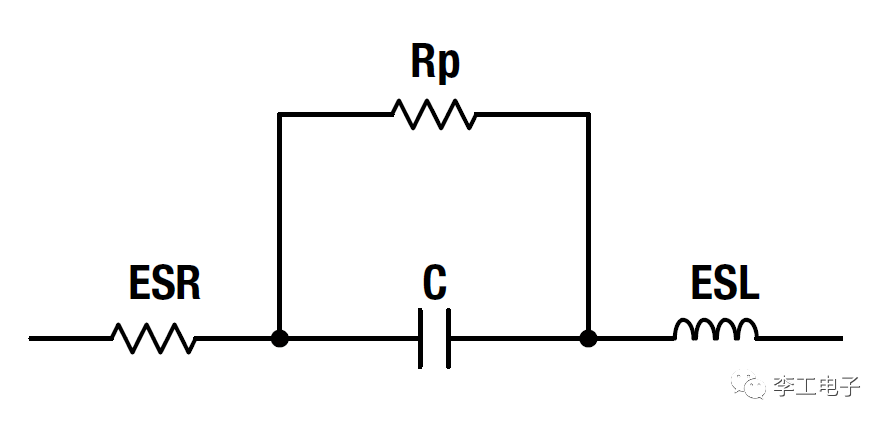
電容器實際模型

這就要從電容器的基礎(chǔ)模型講起，其中有一個常用的參數(shù)： 等效串聯(lián)電阻（ESR），它隨著信號頻率的增大而變小 。當信號頻率接近電容器的“截止”頻率（-3dB滾降點）時，電容器的ESR開始快速變小。

電容器截止頻率的計算方法：

fc=1/（2π?Rf?Cf） ；

假設(shè)信號頻率遠遠低于電容器的諧振頻率（f＜＜fc），可以把電容器的ESR近似看成無窮大 。

運放的增益（G）計算公式為：

G=Rf/R1+1 ；

假設(shè)信號頻率達到甚至超過了電容器的截止頻率（f＞＞fc），在電路中可以把Cf看成是一個與Rf并聯(lián)的電阻（ESR） ，隨著ESR的逐漸減小，Rf/R1的比值也在變小，導致運放的增益下降。

而隨著ESR的不斷減小，從上圖可以看到在10KHz~100KHz的頻率范圍內(nèi)，運放增益迅速下降； 當ESR接近0時，該運放電路變成電壓跟隨器，此時增益為0（1:1信號放大） 。

隨著信號頻率繼續(xù)增加，最后達到了運放的帶寬限制，此時的增益就非常小了。

增加了濾波器的反向配置

了解清楚同相配置以后，我們接著來看反向配置。 根據(jù)運放輸入端電壓相等（動態(tài)平衡）原則，當信號頻率低于電容器的截止頻率（f＜fc）時，可以暫時忽略Cf的存在 。

此時運放的增益（G）計算方法為：

G=－Rf/R1 ；

電容器截止頻率的計算方法與同相的計算方法一致，截止頻率與電容器本身特性和Rf有關(guān)：

fc=1/（2π?Rf?Cf） ；

與同相配置的頻率響應稍微有些區(qū)別，當輸入信號的頻率到達電容器的截止頻點時，運放增益同樣會迅速下降。 對比同相的頻響曲線，當信號頻率在1MHz左右時，并未出現(xiàn)0增益的平臺 。

因為反相配置的電路結(jié)構(gòu)不同， 當ESR（電容Cf的等效串聯(lián)電阻）與Rf的并聯(lián)電阻接近0時，由于運放正向接地，因此輸出基本為0 ，運放的增益很低。

最后，我們可以根據(jù)這兩種運放電路的特點，適當調(diào)整Cf濾波器的截止頻率，即可在可控的范圍內(nèi)讓有用的信號放大，把一部分干擾信號的增益盡可能的降低，這就是運放初步的降噪技術(shù) 。

因此在實際電路應用中，運算放大器與濾波器，無論少了誰都不完整。