函數迭代是數學中一個非常重要和有趣的主題，它在不同的領域有著不同的應用和著眼點。在動力系統中，函數迭代可以揭示復雜系統的演化規律和混沌現象；在計算數學中，函數迭代可以求解各種非線性方程和優化問題。

1

離散動力系統這門學科的主要任務就是研究“函數迭代”。自然，這里的“函數”是在最廣泛的意義上理解的，即它的定義域可以是任何“空間”——帶有某個數學結構的一類集合。當然，最簡單的空間就是實數軸上的單位區間或坐標平面上的單位圓周，即便對于這樣“簡單”的空間所對應的“一維離散動力系統”，其主題卻可以寫成一本有五百頁的大書，需要的數學語言來自分析、拓撲、幾何、代數等幾乎所有現代數學的分支。

在離散動力系統的范圍談論函數迭代，討論的重點是不動點和周期點的穩定性問題，探索的目光聚焦在迭代點軌道的最終性態，而混沌學家則更感興趣于最終走向不可預測的不規則行為，并由此進一步用概率統計的工具研究所有這些行蹤詭異的軌道的整體性質。這些都是我在前幾篇文章中試圖向讀者介紹的基本概念和知識。

然而，在出發點和目的性完全不一樣的另一個極其有用的數學領域——計算數學里，“函數迭代”同樣扮演著不可或缺的角色。“計算數學”，顧名思義，就是以計算為特征的數學，它設計可行、快速、有效、穩定的算法，通過電子計算機的程序實現，數值求解科學技術中建立起來的各類方程：常微分方程、偏微分方程、積分方程或一般的算子方程。離散化這些“連續性方程”就得到線性或非線性的代數方程組，求解這些方程組的一個主要方法就是“迭代法”。

與離散動力系統研究函數迭代的多重目的不太一樣的是，計算數學研究迭代的目標很一致：尋求迭代軌道的收斂性及其速率。為此，計算數學領域里的學者談到迭代時對周期點幾乎是“冷若冰霜”的，因為它導致迭代法不收斂，這不是計算數學家和工程學家所樂見的。所以當我們從計算數學的觀點看函數迭代時，我們的注意力只需放在迭代軌道收斂性這點上。

四十一年前，我在南京大學數學系修讀計算數學最優化理論與方法碩士研究生的第一門專業基礎課是“非線性方程組的迭代解”，選用的教材是馬里蘭大學數學系James M. Ortega和Werner C. Rheinboldt 于1970年出版的Iterative Solution of Nonlinear Equations in Several Variables（多變元非線性方程的迭代解），分兩學期學完。第一學期由老師講授課程，第二學期由學生分章報告，我們的收獲很大，我甚至做了書中全部習題。五年后，在密歇根州立大學讀博士學位的課程時，由于修了李天巖教授一門“[0, 1]上的遍歷理論”學年課程，我對離散動力系統中的“函數迭代”產生了興趣，第二年寫的博士論文居然與計算遍歷理論掛上了鉤。可以說，在我求學成長的歲月中，我先后戴著計算數學和動力系統的面具，學過兩次“函數的迭代”。

學過的知識有用，就沒有白學。這兩種“函數迭代”的理論都對我的研究論文有過貢獻，所以算是做到了“學以致用”。但是現在的我多了一個想法：將自己年輕時代學來的有用知識服務于公眾，傳播更多的數學真理。在這篇文章里，我將向對科學計算感興趣的人介紹迭代法背后的基本思想。與往常一樣，我們主要考慮區間函數的簡單情形，方便大家理解。

2

假設G是定義在一個區間I上的連續函數，并將I映到自身，這樣在I中取定一個初始點x0，由此出發，就可以周而復始地迭代下去得到迭代點數列

x0, x1, x2, …, xn, …，

記為{xn}，其中第n個迭代點xn是G在第n-1個迭代點xn-1的值，即

xn= G(xn-1), n = 1, 2, …; 給定x0。

如果將n個G復合起來的復合函數記為Gn，則xn= Gn(x0)。由于函數G連續并將I映入I，函數Gn也連續且將I映入I。

計算數學家對函數迭代的基本要求是：迭代點數列{xn}必須收斂。在討論這個數列何時收斂的問題前，我們先問另一個問題：假設{xn}確實收斂到I中的一點，這個極限點會有什么性質？或言之，數列{xn}的極限x*與迭代的函數G有什么關系？

注意我們已經假設G在定義域區間I上連續，這個信息加上初等微分學中的連續概念就提供了回答上述問話的線索。連續函數有一個基于數列的等價說法，即函數f在點a連續當且僅當任給f定義域內的數列{xn}，只要它收斂于a，則對應的函數值數列{f(xn)}收斂到f(a)。由迭代程式xn= G(xn-1)可知，兩個數列{xn}和{G(xn-1)}是恒等的數列，既然{xn}收斂到x*，那么{G(xn-1)}也收斂到同一個極限x*。另一方面，由于數列{xn-1}和{xn}一樣收斂到x*，故G在x*的連續性就推出{G(xn-1)}收斂到G(x*)。這樣x*和G(x*)都是{xn}的極限，由收斂數列極限的唯一性，必有x* = G(x*)。這說明，迭代點數列{Gn(x0)}如果收斂到連續函數G的定義域中的一點，則它一定是G的不動點。這個命題的逆否命題可以幫助我們確認何時一個迭代點數列不可能收斂，那就是只要迭代函數G沒有不動點。例如，如果一個人迭代自然指數函數G(x) = ex，則無論他從哪一個初始點出發，迭代點數列都不會收斂，因為不動點方程x = ex在實數集合里無解。

上述簡單結論的一個邏輯后果是，計算數學中迭代法的目的是數值求解不動點方程x = G(x)。如果這個方程根本無解，那就不必構造什么迭代法求解它了，所以在研究迭代法前，要先假設G至少有一個不動點。但是，如果閉著眼睛隨便選取初始點x0開始迭代，能保證{Gn(x0)}收斂嗎？

3

我們先看一個簡單的例子。設G(x) = -x，則G有唯一的不動點0。然而如果我們取任一非零數x0作為初始點迭代G，則得到一個周期為二的軌道：x0, -x0, x0, -x0, …，不收斂到0。對函數G求導數，我們發現在不動點0處，G的導數值的絕對值等于1。如果G(x) = 2x，則對任一初始點x0，易見Gn(x0) = 2nx0，故當xn> 0時，{Gn(x0)}發散到正無窮大，而當xn< 0時，{Gn(x0)}發散到負無窮大，都不收斂到唯一不動點0。注意到對這個G，導數在不動點0的值的絕對值大于1。

我們再看一個例子：G(x) = x – x2。這時G依然只有唯一的不動點0。運用“圖像迭代法”，或通過初等微分學中的“單調收斂定理”可以嚴格證明：當0 < x0?≤ 1時，{Gn(x0)}收斂到不動點0，而當x0?< 0或x0?> 1時，{Gn(x0)}發散到負無窮大。雖然G在不動點0處導數的絕對值等于1，但對不動點右側臨近的初始點，迭代點數列收斂到該不動點。讀者可以用幾何方法畫出一個連續函數y = G(x)的圖像曲線，它與xy-直角坐標系的對角線y = x相切于一點(x*, x*)，在切點的左側，曲線位于對角線上方，向上彎曲；在切點的右側，曲線位于對角線下方，向下彎曲。然后你就會發現，盡管G在x*處的導數絕對值等于1，但從x*左右兩邊附近的任一初始點x0出發的迭代點數列{Gn(x0)}收斂到x*。

這些例子說明，在迭代函數G可求導數的前提下，當G在其不動點x*的導數絕對值等于1時，在其附近出發的迭代點數列可能收斂到x*，也可能不收斂到x*；而當G在不動點x*的導數絕對值大于1時，則根本不能指望迭代點數列會收斂到x*。因此，要想迭代法xn= G(xn-1)生成的數列收斂到G的一個不動點，我們一般需要假設G在這個不動點的導數絕對值嚴格小于1。雖然這個假設不是迭代法收斂的必要條件，但確實是保證收斂的一個充分條件。它的證明不難，也容易理解，但需要對導數的極限定義有透徹的理解。

許多人號稱學過微積分，但可能還需要溫故一下微積分學中最基礎性的概念——極限，所以我們先來回憶一下函數在一點的極限的精確定義：函數f當自變量x趨向于數a時有極限L，是指對于任意給定的正數ε，存在正數δ，使得只要位于f定義域內的x減去a的絕對值大于0但又小于δ，其對應的函數值f(x)減去L的絕對值就會小于ε。用數學的符號，就是要找到δ，使得若不等式0 < |x – a| < δ成立，則不等式|f(x) – L| < ε也成立。

由于函數的導數是通過函數的平均變化率的極限來定義的，函數f在其定義域內一點a的導數f’(a) = limx → a(f(x) – f(a))/(x-a)按照上面的“ε-δ”語言來說就是：任給正數ε，存在正數δ，使得對f定義域內的所有x，不等式0 < |x – a| < δ推出不等式

|(f(x)–f(a))/(x-a) – f’(a)| < ?ε。

好了，我們用上面的導數定義來證明關于迭代法收斂性的一個基本定理：設想迭代函數G在其定義域區間內部有一個不動點x*并且在該點有導數。如果|G’(x*)| < 1，則存在以x*為中點的一個小區間(x* - δ, x* + δ)，使得任取此區間中的一點x0作為初始點，迭代點數列{Gn(x0)}中的所有點都在同一區間內并且lim?n → ∞?Gn(x0) = x*。

在讀懂下面的解析證明之前，不知道這個命題的讀者可用圖像迭代法看到迭代點的收斂性。我們現在嚴格證明之。首先因為x*位于G的定義域區間的內部，存在一個正數δ0使得區間(x*-δ0, x*+δ0)包含在G的定義域中。由假設條件，可取ε = (1 - |G’(x*)|)/2 > 0。對于這個正數，上述的導數定義告訴我們，存在正數δ ≤ δ0，使得滿足不等式0 < |x – x*| < δ的所有點x也滿足不等式

|(G(x)–G(x*))/(x-x*) – G’(x*)| < ?(1 - |G’(x*)|)/2。

由于G(x*) = x*，上式可以改寫成

|(G(x)–x*)/(x-x*) – G’(x*)| < ?(1 - |G’(x*)|)/2。

運用代數不等式 |a| - |b| ≤ |a – b|，就可推出 |G(x*)-x*|/|x-x*| - |G’(x*)| < (1 - |G’(x*)|)/2。故

|G(x)-x*|/|x-x*| < |G’(x*)| + (1 - |G’(x*)|)/2 = (1 + |G’(x*)|)/2。

記r = (1 + |G’(x*)|)/2，則正數r < 1。上面的不等式即為

|G(x)-x*| < r |x-x*|， 任給(x*-δ, x*+δ)中的點x。

因為r小于1，此不等式說明，當初始點x0屬于(x*-δ, x*+δ)時，第一個迭代點x1= G(x0)也在(x*-δ, x*+δ)之中，故同一不等式保證第二個迭代點x2= G(x1) = G2(x0)繼續落在(x*-δ, x*+δ)當中，且有|x2– x*| < r |x1?– x*| < r2?|x0?– x*|。推而廣之，我們知道所有迭代點xn?都在區間(x*-δ, x*+δ)之內，并滿足不等式

|xn– x*| < rn?|x0?– x*|，n = 1, 2, 3, …。

因為limn → ∞rn= 0，結論就是：迭代點數列{xn} 趨向于x*。

4

我們證明了G在不動點x*的導數絕對值小于1是迭代法xn= G(xn-1), n = 1, 2, …具有“局部收斂性”的一個絕對重要的充分條件，這里的“局部”意指當初始點充分靠近x*時就能獲得收斂性。更進一步，這個收斂的快慢程度也與|G’(x*)|有關：此值越接近于0，則收斂得越快。自然，最理想的值應該就是0了，這時的收斂速度超過了像趨向于0的等比數列{rn}那樣的“線性收斂”，所以被稱為“超線性收斂”。

那么，有名聞遐邇且至少具有超線性收斂的迭代法嗎？當然有，而且只需要初等微分學中的泰勒公式就可以構造出許多更高收斂階的迭代法。然而一般而言，如同俗語所述，“一分耕耘一分收獲”，要獲得高階的迭代法，成本也是可觀的，計算數學中的“成本”是用“計算工作量”來衡量的。不過，我們幾乎都聽過一個大名鼎鼎的迭代法，甚至和它常打交道，這就是名字掛的是“牛頓”但實際上應該是“辛普森”的“牛頓迭代法”。

牛頓迭代法用于數值求解非線性方程，它的基本思想用幾何表達最直觀易懂。解方程f(x) = 0的幾何意義就是找到函數y = f(x)的圖像與x-軸的交點。在函數f可求導且導數值都不為零的條件下，設x*是方程的一個解，但我們卻不知道它是幾，于是我們先取一個初始點x0作為x*的一個猜測。自然f(x0)一般不恰好為零。在圖像上的點(x0, f(x0))處作曲線的切線，根據導數的幾何解釋，這根切線的斜率是f’(x0)。由直線的點斜式方程可知，切線的方程是y – f(x0) = f’(x0)(x – x0)，在此方程中令y = 0而解出未知數x的值 x1= x0- f(x0)/f’(x0)，它就是切線與x-軸的交點的x-坐標，當x0距離精確解x*不遠時應該比x0更靠近x*。對x1重復做上面的事，得到比x1離x*更近的點x2。由此類推，有了下列求解方程f(x) = 0的牛頓迭代法：

xn= xn-1– f(xn-1)/f’(xn-1)，n = 1, 2, 3, …。

如果將原方程f(x) = 0改寫成與之等價的不動點方程x = x – f(x)/f’(x)，那么上述的牛頓法就是用于后一個方程的直接迭代法 xn= G(xn-1), n = 1, 2, …, 其中G(x) = x – f(x)/f’(x)。為了研究牛頓法的收斂速率，我們需要假定f的二階導數在x*存在，這樣就保證了迭代函數G在x*處一階導數的存在性。求導數的商法則給出

G’(x*) = 1 – [f’(x*)2– f(x*)f’’(x*)]/f’(x*)2= f(x*)f’’(x*)/f’(x*)2= 0，

理由是f(x*) = 0。根據上面證明出的迭代收斂基本定理，存在以x*為中心的某個開區間(x*-δ, x*+δ)，使得只要初始點x0取之于它，牛頓法產生的迭代點數列{xn}不僅收斂到解x*，而且收斂速率是超線性的。事實上，在關于二階導數稍微更強一點的條件下，牛頓迭代是二階收斂的。

5

到目前為止講到的迭代收斂都是局部性的，那怎么擴大保證收斂的初始點范圍呢？當然，有不少途徑，其中一個十分簡單，但對導數的要求卻頗為苛刻。既然簡單，便適合在這里提及。應用這個方法需滿足的條件是：將定義域區間[a, b]映到自身的迭代函數G有一個不動點x*，且導數處處存在并滿足不等式|G’(x)| ≤ r，其中r為小于1的一個正數。

若條件成立，則對[a, b]中的任一初始點x0，由微分學里的拉格朗日中值定理，

G(x0) – x* = G(x0) – G(x*) = G’(c)(x0– x*)，

其中c是位于x0和x*之間的一個數。這樣，

|G(x0) – x*| = | G’(c)(x0– x*)| = |G’(c)| |x0– x*| ≤ r |x0– x*|，

即G(x0)不僅位于[a, b]，而且比x0更靠近x*。用歸納法，得到

|Gn(x0) – x*| ≤ rn|x0– x*| → 0。

因此，迭代點數列{Gn(x0)}收斂到x*。

如果我們再看一次證明就會發現，施加于導數的要求事實上是為了實現不等式

|G(x) – G(x*)| ≤ r |x – x*|，任給定義域[a, b]中的點x。

只要這個不等式滿足，該迭代法對任意初始點都會收斂。然而該不等式并不要求G必須可導，甚至也不需要G在x ≠ x*處連續。當然，用于迭代的函數一般都是至少連續的，所以可以將上述不等式中的特殊點x*改為與x有同等地位的y，即

|G(x) – G(y)| ≤ r |x – y|，任給閉區間[a, b]中的點x和y，

其中G將[a, b]映到自身，且0 < r < 1。滿足這些條件的G稱為在區間[a, b]上是壓縮的。區間上的壓縮函數是處處連續的，但不一定處處可導。壓縮函數一定存在不動點，因為這是“壓縮”性質的一個直接推論，證明的基本思想來自公比絕對值小于1的等比級數的收斂性和實數的完備性這兩個事實，細說如下：

在區間[a, b]中任取一點x0迭代G，得迭代點數列{xn}，其中xn= G(xn-1) = Gn(x0)。則對任意正整數n有

|xn+1– xn| = |G(xn) – G(xn-1)| ≤ r |xn– xn-1|。

累次使用上述過程，就有 |xn+1– xn| ≤ rn|x1– x0|。從而對任意自然數p，由代數中的三角不等式及已得的不等式，

|xn+p– xn| ≤ |xn+1– xn| + |xn+2– xn+1| + … + |xn+p– xn+p-1|

≤ (1 + r + … + rp) |xn+1– xn| ≤ rn|x1– x0|/(1-r)。

既然limn → ∞rn= 0，上式右端數列的極限為0，說明{xn}是一個柯西數列，即雙下標數列{|xm– xn|}當m和n都趨于無窮大時的極限為0。因為在實數集內，任何柯西數列都是收斂的，故極限limn → ∞xn= x*存在。由于對所有n都有a ≤ xn≤ b，極限x*屬于[a, b]；由于G處處連續，x*是G的不動點。如果在幾行之上的不等式中取p → ∞時的極限，我們還可以得出迭代到第n步后的“誤差估計”：

|x* – xn| ≤ rn|x1– x0|/(1-r)，

這是計算數學家和工程師最愛看到的結果。

更進一步，壓縮函數不僅有不動點，而且僅有一個不動點，因為如果有相異不動點x*和y*的話，則 |x*- y*| = |G(x*) – G(y*)| ≤ r |x* - y*|，因為x* - y* ≠ 0及r < 1，這個不等式是不可能的。這個唯一性是許多其他著名的不動點定理如“布勞威爾不動點定理”所缺乏的，一維的布勞威爾不動點定理本質上就是微分學里的介值定理，它只要求函數連續，所以少了一點限制條件，不動點的個數就有可能大于一。這和家長對孩子讀書的框框條條效果類似，限制越多，自由越少，子女今后的成就也就可能越少。

6

在數學上，“唯一性”是很重要的一條性質，因此壓縮函數的概念被抽象成泛函分析中所謂“距離空間”內的“壓縮映射”。這門學科的集大成者、波蘭利沃夫數學學派的領袖巴拿赫 (Stefan Banach，1892-1945)，在他進入而立之年時，提出了一個“壓縮映射定理”，現在該定理又以它的創立者命名為：巴拿赫不動點定理。其專業性陳述是這樣的：

令(X, d)為一個完備的距離空間。若G: X → X為一壓縮映射，即存在小于1的一個數r，使得

d(G(x), G(y)) ≤ r d(x, y)

對X中所有的元素x和y都成立，則G有并只有一個不動點x*，且從X中任一初始點x0出發的迭代點列{Gn(x0)}收斂到x*，其第n個迭代點的逼近上界為

d(x*, xn) ≤ rnd(x1, x0)/(1-r)。

這幾個抽象術語自然需要解釋，但只要發現上面定理的內容，包括條件結論中的兩個不等式，與之前實變量的壓縮函數幾乎是一個模式，就會知道巴拿赫不動點定理理解起來一點也不難。這也充分說明任何抽象理論都源自簡單的具體模型。

首先，什么是距離空間？“距離”是我們日常生活中司空見慣的幾何概念，這個量不能為負，與度量距離的兩點次序無關，而且兩點之間的距離為零當且僅當這兩點重合。距離還有一個關鍵的性質：北京和南京之間的距離肯定不大于北京和揚州的距離加上揚州和南京的距離。據說這個被稱為“三角不等式”的性質連聰明的狗都可透徹理解，否則它們一見主人就不會沿著人狗連線的方向直奔而來。顯而易見，實數軸上兩點x和y之間的距離等于非負數|x – y|，用符號d(x, y)表示，其中“d”是距離的英文單詞distance的首字母。這樣我們可以將任意一個實數的集合A，比如一個區間，連同這個距離d組成的“二元組”(A, d)稱為距離空間。同樣，任意抽象集合X連同一個定義在其上的距離函數d，合起來的(X, d)就稱為一個距離空間，其中距離函數d滿足通常名詞距離對于我們已經習以為常的如下性質：對X中任意的元素x, y, z， (1)d(x, y) ≥ 0且d(x, y) = 0當且僅當x = y； (2)d(x, y) = d(y, x)；

(3)d(x, y) ≤ d(x, z) + d(z, y)。

其次，什么叫“完備”的距離空間？在微積分中用兩數x和y之間的通常距離|x – y|可以定義數列的收斂性：數列{xn}收斂到數x，假如距離數列{|xn– x|}當n趨于無窮大時趨向于0。用完全同樣的方式可以定義距離空間(X, d)中元素序列的收斂性：我們說X中的序列{xn}收斂到X的一個元素x，如果距離數列{d(xn, x)}當n趨于無窮大時趨向于0。類似地，實數集合中的柯西數列也可直接推廣到距離空間中的序列：X中的序列{xn}被稱為是柯西序列，若雙指標數列{d(xm, xn)} 當m和n都趨于無窮大時趨向于0。我們知道在實數中任何柯西數列都有極限，但并非每一個距離空間都有這一性質，就像有理數組成的柯西數列不一定收斂到有理數那樣。如果一個距離空間(X, d)中的每一個柯西序列都有極限，那么(X, d)稱為是完備的。

既然閉區間是我們大學時代就熟悉的一個代表性完備距離空間，上面關于壓縮函數的不動點定理的全部證明，只要將絕對值符號改為距離符號，完全就可以移植為巴拿赫不動點定理的證明，讀者可以自行寫出這一證明。巴拿赫不動點定理的一個標準應用是常微分方程初值問題解的存在唯一性定理證明，這時初值問題的解被表達成將連續函數映成連續函數的某個積分算子的不動點，這里定義在某個閉區間[a, b]上的所有連續函數全體構成一個距離空間，它的距離函數定義為d(f, g) = max{|f(x) – g(x)|: a ≤ x ≤ b}。

7

再回到牛頓迭代法，我們已知它總是局部收斂的，但如果初始點取得距離方程f(x) = 0的解x*太遠了，那會有什么結果？牛頓法非局部的收斂性問題是一門大學問，蘇聯數學家康特諾維奇 (Leonid Kantorovich，1912-1988) 于上世紀中葉發展了半局部收斂理論，在James M. Ortega和Werner C. Rheinboldt的那本名著中有詳細的討論。該理論的特點是，即便初始點沒能選在保證局部收斂的局部收斂域內，只要某些關鍵不等式被滿足，就能保證迭代點的序列收斂到方程的解。自然，許多初始點卻滿足不了這些條件，容易構造一個例子，在許多點出發的牛頓迭代數列發散，如下圖所示。

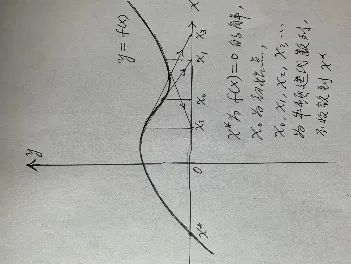
事實上，讓牛頓法不收斂的那些初始點可以形成復雜無比的點集。上世紀80年代的某個學期，康奈爾大學數學教授哈伯德 (John Hubbard，1945-) 在法國一所大學度學術假，同時給一年級新生講授一門微積分課程。有次他靈光一閃，將自己從事的一部分事業——復離散動力系統——和計算數學中古老的牛頓法聯系在一起。復離散動力系統，顧名思義，就是迭代復變函數看看最終走向如何。

中學生就已經知道像 2 + 3 i這樣的復數是什么，這是幾百年前為了迎合求解二次方程 x2+ 1 = 0 的需要不得不創造出來的“虛無縹緲”之數。這“由實數到虛數”的一個大跳，解決了許多數學大問題，例如代數基本定理——在復數范圍內，每個代數方程都有根。復動力系統和分形幾何這兩門當代學科緊密相連。

教授了太多次微積分課本里介紹的牛頓法，有點厭倦標準教法的哈伯德想換一換花樣。他把目光轉向在復數平面上用牛頓法解最簡單的三次方程z3– 1 = 0，即算出1的三個立方根，分別是實數1和兩個互相共軛的復數(-1 + i√3)/2 和(-1 - i √3)/2。這三個根在復平面上形成一個等邊三角形。任取一個復數作為初始點，他讓學生們看看牛頓法將引向三個根中的哪一個。這個創造性的習題給學生鋪下了一條發現之路！

自然，根據牛頓法的局部收斂性，當初始點取得靠近三根之一時，迭代點復數列將收斂到那個根。但是，哈伯德讓學生用計算機編程找出復平面上哪些初始點將走到第一個根，哪些點趨向于第二個根，哪些點會導致第三個根。這三類初始點分別用三種不同的顏色區別開來。在粗糙的選點下，牛頓法迭代的最終性態果然如他所猜把平面分成三個扇形，但隨著選點越來越精細，他和學生們發現這三個區域的分界線越來越不清楚：三種顏色互相纏繞，只要兩種顏色靠近一些，第三種顏色便乘虛而入，擠進來夾在它們中間，就好像紅黃藍三股繩絞在一起彼此糾纏不清。這又引起一連串新的自相似的涌入，似乎沒有哪個點可以分開任意兩種顏色。就這樣，美國數學教授哈伯德和修其課程的法國大學生們意外地發現了已經廣泛使用了幾百年的牛頓法所制造的分形圖。

當然，這個漂亮的牛頓分形圖令研究動力系統的學者興高采烈，卻令冀望算法收斂的計算數學家愁眉苦臉，因為他們看到即便像牛頓法這樣優秀的迭代法，不產生收斂迭代序列的那些初始點，看上去是如此的復雜！從而，在計算數學領域，迭代法的收斂性一直是引人注目的課題。






審核編輯：劉清