摘要：背包問題(Knapsack problem)是一種組合優化的NP-Complete問題。問題可以描述為：給定一組物品，每種物品都有自己的重量和價格，在限定的總重量內，我們如何選擇，才能使得物品的總價格最高。

背包問題早期的研究可追溯到1897年，數學家托比亞斯·丹齊格（Tobias Dantzig，1884-1956）提出如何包裝最有價值或有用的物品而不會超載行李的問題。使用傳統的計算機算法來解決這個問題時，解決問題所需的時間隨著問題規模變大將呈指數級增長。

因此，對于大規模的問題，需要使用更高效的算法、近似算法或其他有效的工具來解決。背包算法一般提法是：一位旅行者攜帶背包去登山，已知他所能承受的背包重量限度為akg，現有n種物品可供他選擇裝入背包，第i種物品的單件重量為aikg，其價值（可以是表明本物品對登山的重要性的數量指標）是攜帶數量xi的函數ci(xi)(i=1,2,...,n)，問旅行者應如何選擇攜帶各種物品的件數，以使總價值最大。相似問題經常出現在商業、組合數學，項目選擇，資本預算，計算復雜性理論、密碼學和應用數學等領域中。

目前，許多背包問題的理論研究已經廣泛應用在現實生活中，幫助大量面向應用程序的研究人員與從業者尋找更好、更快的解決方案來解決巨大的問題。通常，背包問題是更復雜的組合問題的子問題的優化問題，大多數需要選擇某些給定的子集來獲得利潤總額最大化的項目，而分配的總重量不超過背包的容量。

背包問題在現實生活中的應用包括財務建模、生產和庫存管理系統、分層抽樣、制造中的排隊網絡模型設計以及制造中的流量過載控制電信系統。其他應用領域包括產量管理、航空公司、酒店和租賃機構、大學招生、質量適應和交互式多媒體系統的準入控制、貨物裝載、資本預算、削減庫存問題，以及巨大的分布式計算機處理分配系統。

北京玻色量子科技有限公司在5月16日新品發布會上推出的100計算量子比特相干光量子計算機真機——“天工量子大腦”，旨在快速、高效地求解NP-hard的Ising模型。背包問題可以轉化為一個Ising/QUBO模型，“天工量子大腦”可以極大簡化求解步驟并在毫秒級的時間內給出問題的全局最優解。

問題描述

背包問題是基本的組合優化問題，我們引入這個背包問題的二次版本進行分析，二次指物品之間的選擇關系會影響物品的價值取值，即二次背包問題（Quadratic KnapsackProblem），該問題是經典的NP-Hard問題之一。

建模思路

首先給出二次背包問題的混合整數規劃模型

其中xj表示是否選擇物品j，xj=1表示選擇，否則表示不選擇，vij是物品i,j的交互價值，aj為物品j的體積，b為背包的容量限制。我們引入懲罰系數P和m+1個0/1松弛變量yk,k∈{0,...,m}將模型轉寫為QUBO模型。

首先將不等式約束配平得到式（2）

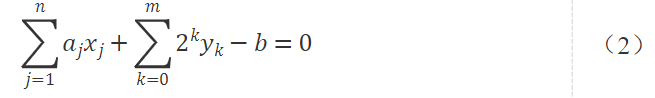
將式（2）平方后乘上懲罰系數即可以轉為無約束的表達，得到式（3），即該問題的QUBO模型

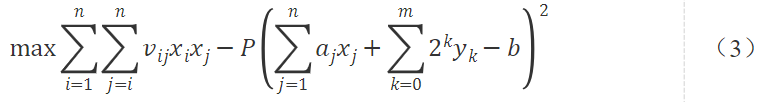
我們用下面的例子來進一步分析。

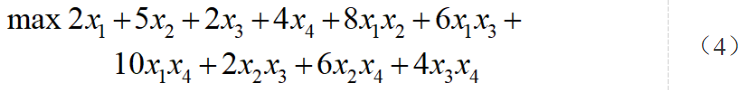
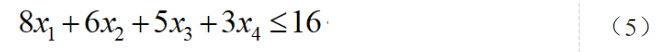
其中式（5）為不等式約束，舉例而言，如不等式a-b<0可以通過引入輔助變量c轉化為等式a-b+c=0,c>0，其中c也叫做松弛變量，我們引入輔助松弛0/1變量x5,x6來配平式（5）。

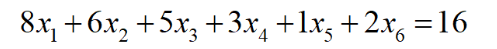? （6）

因此，我們得到QUBO模型為：

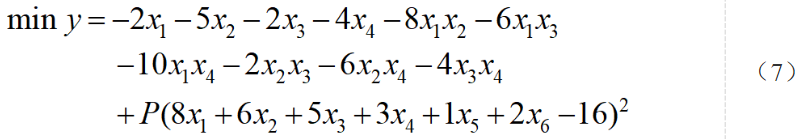
我們取P=10，同時根據x2=x（x為0/1變量）的特性，我們可以化簡式子，舍去常數項2560后，我們得到QUBO模型的矩陣表達：

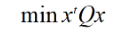? ? ? ? （8）

其中Q矩陣為：

求解這個QUBO模型，我們可以得到最優解

x1=x3=x4=1,x2=x5=x6=0,y=-2588。

問題拓展

背包問題是經典的NP-hard問題，在數學、計算機科學、物理學等領域都有應用。該問題有多個擴展和變種，其中一些常見的包括：

多重背包問題（Multiple Knapsack Problem）：在多重背包問題中，每種物品有多個可用的副本，而不僅僅是一個。每個物品的數量限制可能不同，目標是選擇物品的副本來最大化總價值。

無界背包問題（Unbounded Knapsack Problem）：在無界背包問題中，每種物品有無限多個可用的副本。目標是選擇物品的副本來最大化總價值。

分數背包問題（Fractional Knapsack Problem）：在分數背包問題中，物品可以被分割成任意比例，可以選擇部分物品放入背包中。目標是選擇物品的比例來最大化總價值。

有約束背包問題（Constrained Knapsack Problem）：在有約束背包問題中，除了背包容量限制外，還存在其他約束條件，如物品之間的依賴關系、物品的數量限制等。目標是在滿足所有約束條件的前提下，選擇物品來最大化總價值。

未來，玻色量子將依托100計算量子比特相干光量子計算機真機——“天工量子大腦”，聚焦“實用化量子計算”，不斷深入研究更多NP-Complete問題，拓展更多可實用化量子計算的真實應用場景。

玻色量子還將啟動“燎原計劃”開發者平臺，并持續對外開放“天工量子大腦”的真機測試，熱忱歡迎更多不同領域的研究伙伴前來了解相干量子計算的原理和能力，在此基礎上展開共同研發，用量子計算去解決更多真實場景中的問題，讓量子計算的超強算力能真正服務于各行各業，滿足未來時代對于計算的需求。

審核編輯：劉清