Delta-Sigma ADC與奈奎斯特速率ADC的工作方式略有不同。它依賴于過采樣和噪聲整形來實現高分辨率轉換。
我之前的文章, 了解逐次逼近寄存器ADC,證明了這種奈奎斯特速率架構的弱點:它的精度和線性度以及最大有效分辨率受到DAC等模擬元件不完善的限制。
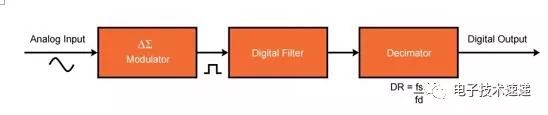
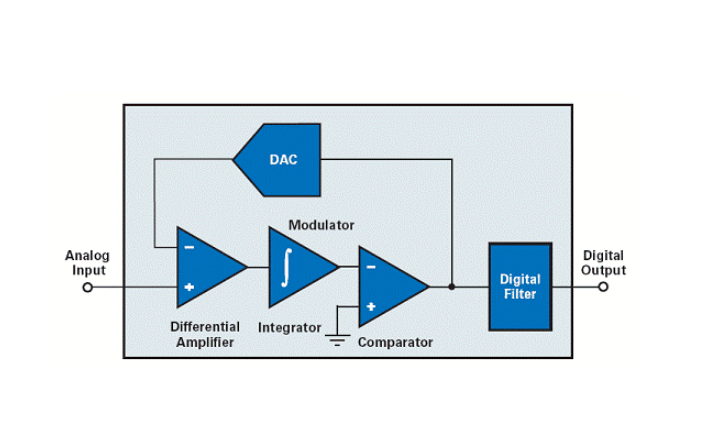
Delta-Sigma ADC所屬的過采樣轉換器系列旨在克服奈奎斯特速率轉換器的局限性。Delta-Sigma ADC由調制器,濾波器和抽取器組成,如下所示。Delta-Sigma ADC的數字化率約為75%。
通過引入更復雜的數字電路和過采樣數據,他們試圖降低對精確模擬元件的要求,這些元件可被視為其他ADC架構的限制因素。
過采樣
為了理解過采樣的概念,需要在頻域中進行分析。
如果我們考慮數據轉換器輸入端的正弦波示例,根據奈奎斯特準則,最小采樣頻率定義為信號帶寬的兩倍。
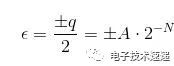
對于我們的正弦波示例,我們看到了感興趣頻率的峰值,但也有很多噪聲,如下所示:
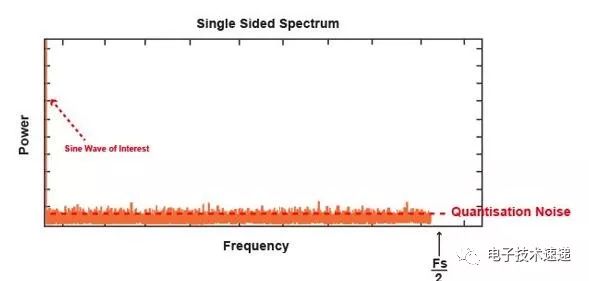
這種噪聲稱為量化噪聲 (PDF),這是由于連續輸入正弦波的樣本只能采用由ADC分辨率決定的有限數量的離散狀態。這種隨機量化誤差存在于奈奎斯特頻帶內,延伸到Fs / 2,可以描述為:
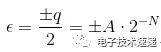
由此,我們可以將信號與量化噪聲比確定為:
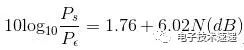
因此,在奈奎斯特速率ADC中,我們通過增加ADC的分辨率(用N表示)來改善SQNR(信號與量化噪聲比)。有關這些公式的更深入解釋,請參閱我之前的文章, 解密分辨率和采樣率。
相反,如果我們現在將過采樣頻率從Fs增加到KF,如下所示,則區域Fs / 2中的量化噪聲減小。SQNR實際上是相同的。
然而,量化噪聲分布在較大的頻率范圍內。通過在Delta-Sigma ADC中集成濾波器,可以消除一些量化噪聲。因此,在感興趣的頻率范圍內量化噪聲的這種減少使得低分辨率Delta-Sigma架構能夠執行高分辨率模數轉換。
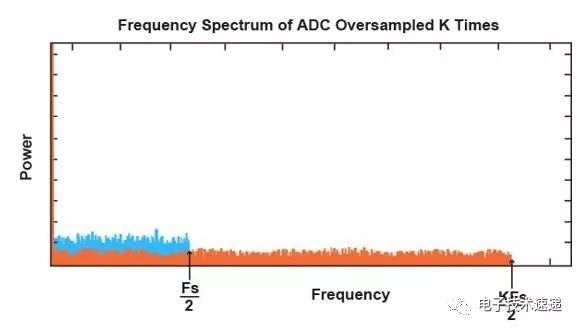
如果我們將采樣率提高4倍,則SQNR會提高6 dB。換句話說,每次我們將采樣率提高四倍時,我們獲得的相當于將ADC的分辨率加1位。僅使用過采樣,為了實現12位分辨率,輸入必須過采樣4 11。或者,更一般地說,對于分辨率的N位增加,我們必須過采樣2 2N因子。
幸運的是,另一種技術稱為噪聲整形,可實現超過6 dB的增益。
噪音整形
一階Delta-Sigma調制器的框圖如下所示。它由差分放大器,積分器,比較器和開關組成。開關或1位DAC將負或正參考電壓切換到放大器的負輸入。
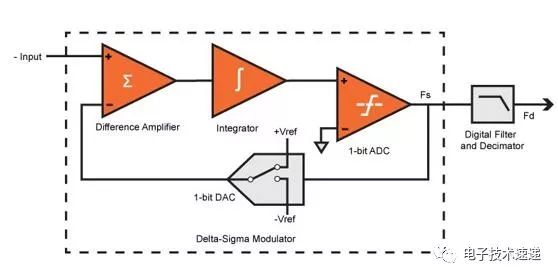
在這種架構中,如果輸入信號增加,1位ADC(只是一個比較器)會產生一個。如果它減少了,它會產生零。因此,Δ-Σ調制器傳輸輸入信號的變化或梯度。
與過采樣一樣,噪聲整形最好在頻域中進行說明。調制器的頻域模型如下所示:
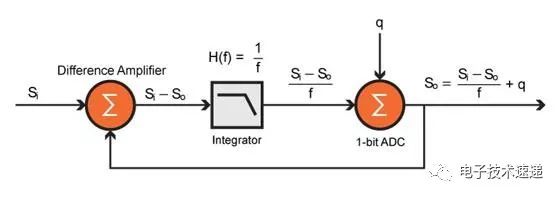
該架構中的積分器充當輸入信號的低通濾波器。由于1位轉換過程,量化噪聲被添加到該濾波器的信號輸出。調制器的輸出可以使用下面的等式表示。
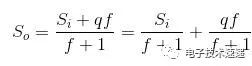
該等式中的第一項可以被認為是信號項,第二項可以被認為是噪聲項。當頻率接近零時,可以看出噪聲項接近零并且調制器的輸出接近S i。隨著頻率增加,噪聲項接近q并且信號項接近零。因此,積分器充當量化噪聲的高通濾波器。
高階Delta-Sigma ADC,在調制器中具有多于一級的積分和求和,可用于實現進一步的噪聲整形。
數字濾波和抽取
Delta-Sigma調制器將噪聲推向更高的頻率,以提高ADC的分辨率,并執行模擬輸入到比特流的轉換。數字濾波和抽取級用于濾除高頻噪聲并將數據速率降低到可用量。
使用的濾波器通常是一種稱為sinc濾波器的平均濾波器。由于噪聲已經被推到高頻,因此低通濾波器響應用于衰減量化噪聲。因此,已經獲得了原始信號的高分辨率版本。
濾波器的輸出數據速率與采樣速率(Fs)相同。濾波器降低了信號的頻率帶寬。因此,根據奈奎斯特準則,大多數樣本不包含任何有用的信息。
抽取是丟棄不必要的樣本的過程,并且用作將數據速率降低到可用值同時根據奈奎斯特準則維護信息的機制。
Delta-Sigma ADC具有兩種采樣率,即輸入采樣率(Fs)和輸出數據率(Fd)。Fs與Fd的比率稱為抽取率(DR)。通過降低濾波器的通帶并增加DR,同時保持相同的Fs,可以增加Delta-Sigma ADC的有效位數(ENOB)。同樣,ADC的帶寬可以以ENOB為代價來增加。
-
濾波器
+關注
關注
161文章
7953瀏覽量
180024 -
寄存器
+關注
關注
31文章
5394瀏覽量
122334 -
差分放大器
+關注
關注
8文章
496瀏覽量
52603 -
調制器
+關注
關注
3文章
880瀏覽量
45720 -
ADC轉換器
+關注
關注
1文章
28瀏覽量
8428
發布評論請先 登錄
相關推薦
Sigma-Delta ADC常見問題解答
高分辨率、低漂移和精密稱重天平電子秤解決方案
請問24位的分辨率是否是所有ADC的極限?
擴展的Delta-Sigma ADC數據表?
單片機內置ADC實現高分辨率采樣的方法
驅動高分辨率 SAR ADC

Delta-Sigma AD轉換器的詳細資料介紹
AN-241:AD7710高分辨率(24位)∑-Delta A/D轉換器評估板

太秀了!單片機內置ADC實現高分辨率采樣?




















評論