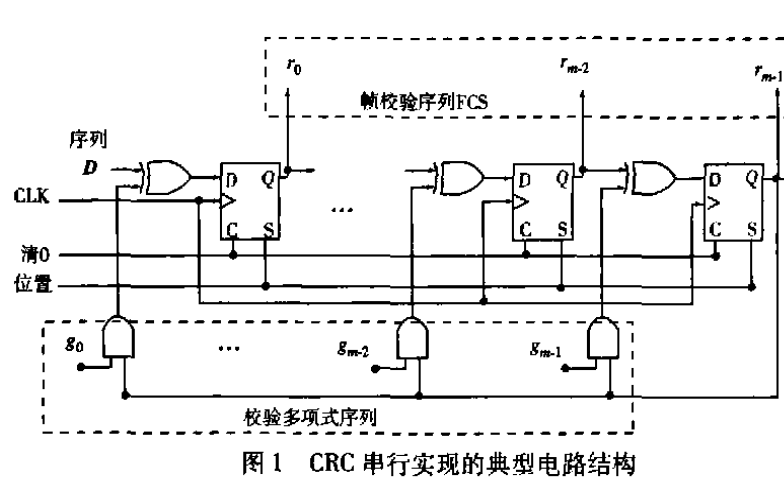
數(shù)據(jù)校驗(yàn)的基礎(chǔ)運(yùn)算原理是模2運(yùn)算，也就是異或運(yùn)算。

簡(jiǎn)單講述一下CRC的原理， CRC校準(zhǔn)首先要確定一個(gè)多項(xiàng)式M(x), 例如

根據(jù)這個(gè)多項(xiàng)式的最高系數(shù)5， 在數(shù)據(jù)后補(bǔ)充5位0. 然后對(duì)新增0的數(shù)據(jù)進(jìn)行模2除法。例如數(shù)據(jù)0010, 根據(jù)上式， M(x)可以寫(xiě)成 110101。那么模2的最終結(jié)果為 11111，那么把這個(gè)運(yùn)算結(jié)果替換為原先補(bǔ)充的5位0，這就是用于校驗(yàn)的冗余碼。這樣輸出傳輸后，接收方利用同樣的多項(xiàng)式運(yùn)算，得到的結(jié)果是0， 即數(shù)據(jù)沒(méi)有傳輸錯(cuò)誤。

更多的CRC內(nèi)容介紹可以網(wǎng)上查詢資料，此處不再贅述。

那么在高速通信中，數(shù)據(jù)以串行傳輸?shù)姆绞皆谕獠總鬏敚窃趦?nèi)部數(shù)據(jù)處理還是以并行數(shù)據(jù)為主。如何實(shí)現(xiàn)CRC硬件計(jì)算的并行化處理呢？

第一種方法，把運(yùn)算過(guò)程實(shí)現(xiàn)，也就是輸入與對(duì)應(yīng)的位數(shù)做異或。然后多次并行例化這個(gè)過(guò)程，把上一輪計(jì)算的結(jié)果作為下一次計(jì)算的輸入。運(yùn)算結(jié)果的流程如下圖：

轉(zhuǎn)成Verilog如下，僅作為一個(gè)例子，未仿真驗(yàn)證過(guò)：

reg [5:0] lsfr_tmp [3:0] ;

genvar i;
generate for (i = 0; i < 4; i = i + 1) begin: cdc_cal
always @ (posedge clk or posedge rst) begin
if (rst) begin 
   lsfr_tmp[i] <= 'd0;
end
else if (i != 0) begin
   lsfr_tmp[i][0] <= lsfr_tmp[i-1][4] ^ data[3-i];
   lsfr_tmp[i][1] <= lsfr_tmp[i-1][0] ;
   lsfr_tmp[i][2] <= lsfr_tmp[i-1][4] ^ data[3-i] ^ lsfr_tmp[i-1][1];
   lsfr_tmp[i][3] <= lsfr_tmp[i-1][2] ;
   lsfr_tmp[i][4] <= lsfr_tmp[i-1][4] ^ data[3-i] ^ lsfr_tmp[i-1][3];
end
else begin
   lsfr_tmp[0] <= 'd0;
   lsfr_tmp[0][0] <= data_in[3] ;
   lsfr_tmp[0][2] <= data_in[3] ;
   lsfr_tmp[0][4] <= data_in[3] ;
end
end
end
endgenerate

assign crc_out = lsfr_tmp[3] ;

這種方法確實(shí)可行，在中間插入流水線的話，數(shù)據(jù)的吞吐率應(yīng)該也不小。

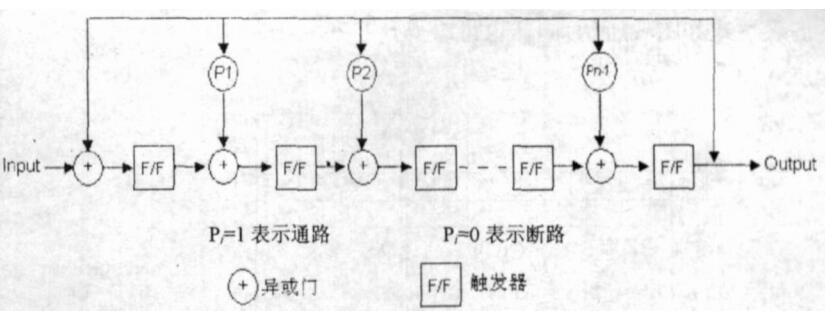
但我們還有第二種方法，根據(jù)多項(xiàng)式的LSFR，推導(dǎo)參考資料[1]可以自動(dòng)生成Verilog代碼如下，得出最終的冗余碼與輸入和多項(xiàng)式之間的映射關(guān)系。

還是以4 bits的數(shù)據(jù)輸入和上面的多項(xiàng)式為例，根據(jù)得到的verilog CRC并行化代碼如下，它的輸出與上一次的CRC冗余碼也存在關(guān)系：

//-----------------------------------------------------------------------------
// CRC module for data[3:0] ,   crc[4:0]=1+x^2+x^4+x^5;
//-----------------------------------------------------------------------------
module crc(
input [3:0] data_in,
input crc_en,
output [4:0] crc_out,
input rst,
input clk);

reg [4:0] lfsr_q,lfsr_c;

assign crc_out = lfsr_q;

always @(*) begin
    lfsr_c[0] = lfsr_q[1] ^ lfsr_q[2] ^ lfsr_q[3] ^ data_in[0] ^ data_in[1] ^ data_in[2];
    lfsr_c[1] = lfsr_q[2] ^ lfsr_q[3] ^ lfsr_q[4] ^ data_in[1] ^ data_in[2] ^ data_in[3];
    lfsr_c[2] = lfsr_q[1] ^ lfsr_q[2] ^ lfsr_q[4] ^ data_in[0] ^ data_in[1] ^ data_in[3];
    lfsr_c[3] = lfsr_q[2] ^ lfsr_q[3] ^ data_in[1] ^ data_in[2];
    lfsr_c[4] = lfsr_q[0] ^ lfsr_q[1] ^ lfsr_q[2] ^ lfsr_q[4] ^ data_in[0] ^ data_in[1] ^ data_in[3];

end // always

always @(posedge clk, posedge rst) begin
if(rst) begin
      lfsr_q <= {5{1'b1}};
end
else begin
      lfsr_q <= crc_en ? lfsr_c : lfsr_q;
end
end // always
endmodule // crc

那么它們之間的關(guān)系是如何得出的呢？根據(jù)參考資料2 提供的資料來(lái)看，關(guān)系的得出如下。

首先，輸入的數(shù)據(jù)以及多項(xiàng)式的值會(huì)影響輸出的結(jié)果。

其次，整個(gè)過(guò)程是模2運(yùn)算，也就是非0即1。那么，可以把輸入數(shù)據(jù)和多項(xiàng)式對(duì)數(shù)據(jù)結(jié)果的影響分開(kāi)計(jì)算，最后整合。且我們可以用獨(dú)熱碼的形式計(jì)算輸入的每一位對(duì)輸出的影響。

因此，首先考慮輸入數(shù)據(jù)對(duì)結(jié)果的影響，將多項(xiàng)式的初始數(shù)值設(shè)為0；輸入數(shù)據(jù)分別設(shè)為0001, 0010, 0100, 1000. 帶入到上圖的LFSR中計(jì)算，最后得到的輸出數(shù)據(jù)為：

然后，設(shè)輸入數(shù)據(jù)為0000， 多項(xiàng)式的初始數(shù)值為00001, 00010, 00100, 01000, 10000；帶入LFSR中計(jì)算，得到的輸出數(shù)據(jù)為：

根據(jù)上述的兩表，可得out[0]跟輸入數(shù)據(jù)0,1,2 bit以及多項(xiàng)式的1，2，3bit有關(guān)。因此做異或運(yùn)算；然后依次類(lèi)推，得到了所有的映射關(guān)系。然后就可以得到上述Verilog中l(wèi)fsr的運(yùn)算關(guān)系了。

當(dāng)然，如果你的CRC的多項(xiàng)式初始數(shù)值默認(rèn)為0，即與之前的CRC校驗(yàn)冗余碼無(wú)關(guān)，那么其實(shí)可以不用計(jì)算多項(xiàng)式數(shù)值的情況，只看第一個(gè)表。現(xiàn)在拿第一個(gè)表的對(duì)應(yīng)關(guān)系，計(jì)算下0010的冗余碼。就是11111.