FIR濾波器在信號處理和通信系統中有著極為廣泛的應用，全稱是有限長單位沖擊響應濾波器。

FIR濾波器的缺點是運算量大，但結合目前的芯片技術，FPGA自然不必說，可以非常靈活的設計很高階次的并行結構，ASIC和GPU都是高密度的流水線型DSP處理，對于FIR所要求的高運算能力，自然是不在話下。另一個缺點在于對于低頻信號處理顯得有一些力不從心。

FIR濾波器的優點在于階次可以做的很高，并且很容易得到各種各樣期望是的響應曲線，很靈活，并且通過調整窗函數，可以得到很好的濾波效果。

FIR濾波器可以說是和卷積相當緊密的聯系在一起的，可以說FIR是完全依托于卷積的概念而生的一種濾波器。并且由于傅里葉前輩的貢獻，我們可以很簡單的用FFT來計算大長度的FIR，也因此在通信系統的信號處理中隨處可見FIR的身影。

濾波

想要把一個知識點發散出去，那就得對它認識的足夠深刻。作為一個硬件工程師，對于濾波的概念再熟悉不過了，所謂濾波，就是濾掉不想要的雜波，留下我們想要的信號。

但是如果我不能給別人講出一點更深層次的東西，也辜負了別人關注我一番。從頻域上來講，信號是一個矢量，濾波的目的在于只保留這個矢量的某些分量，而濾掉其他分量，得到其在子空間內的投影。

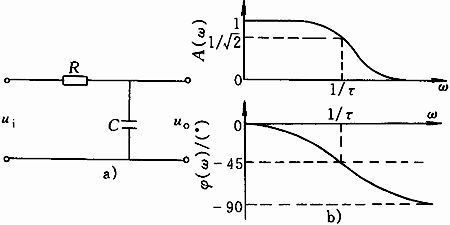
舉個簡單的例子，一階低通濾波。一階低通濾波是怎么實現的？在對輸入信號做了延時之后再疊加回去，就得到了濾波之后的結果。信號在時間上的延時就相當于相位上的滯后，參照上圖的頻率響應曲線。當相位的滯后到了180°時，和原本的信號做疊加，得到的結果就是0，于是就被濾掉了。

把一階低通濾波抽象到離散系統中，采用數字的方式來實現，其數學表達式是Y(n)=a*X(n)+(1-a)*Y(n-1)。這個結果在我大三的計算機控制課上有過詳細的推導過程，但我沒記住，自己推了半天也沒推出來，索性就直接放個結果吧。可以看到，一階低通濾波的本質是把輸入信號和上一次的輸出信號做一個加權，通過調不同的加權系數來調整濾波器的帶寬。

數字濾波器可以認為是直接用數學語言來對信號進行濾波，所以其使用和實現上與電路搭建的濾波器有著本質的差別。例如上面的一階低通濾波，用程序實現的話可以實現任意的帶寬設計，而用RC電路實現就會嚴重受限于器件的工藝。所以把濾波器引申到數字處理之后可以得到這樣的定義：濾波器的本質是對頻率的加權疊加；和期望的響應曲線做相關。這兩句話想不通也沒有關系，下面還會繼續介紹。

卷積

卷積對于工程學來講可以說是大廈的根基一般，往廣義了來講，可以說世界上一切都是卷積的結果。

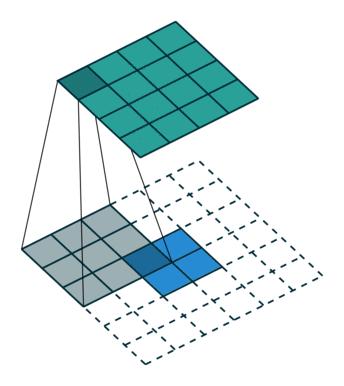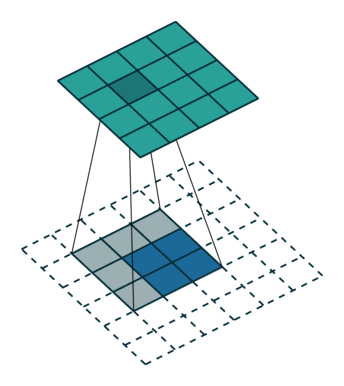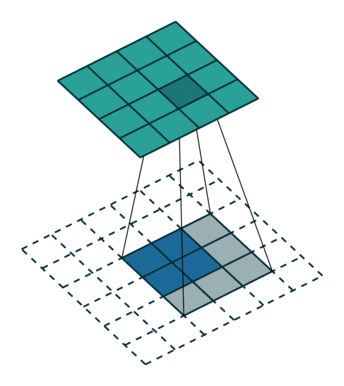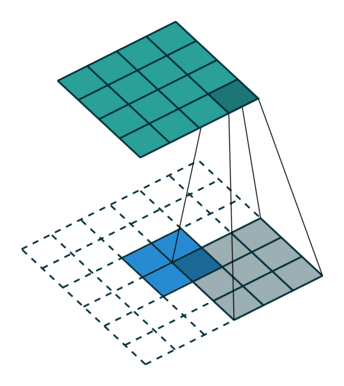
上圖是卷積運算的一個示意圖。那么卷積的物理意義是什么？我看到過很多很多的解釋，但回頭來看，這些解釋，懂得人看起來覺得說的沒問題，不懂的人還是看不懂。我這里舉一個例子來說明什么是卷積：小哪吒很皮，這天偷跑出去，在城里惹了禍，把別人家房子弄塌了，李靖給人賠禮道歉修房子，回到家打了小哪吒一頓，屁股腫了，過了兩天腫消下去了，沒多久又出去惹了禍，抽了敖丙的龍筋，老龍王找上門來，李靖氣的又打了他一頓，屁股又腫了，過了半小時，李靖氣沒消，又打了一頓，老龍王不依不饒，李靖沒辦法又打了一頓，屁股就腫的越來越高。

在這個例子里，小哪吒屁股腫的程度是最終的輸出結果，這個結果不是由李靖的某一巴掌所單獨決定的，而是這一天加起來挨的打所共同影響的結果。從最終的結果來講，第一巴掌的貢獻是最小的，最后一巴掌的貢獻是最大的。這就是加權疊加。而一巴掌的結果，隨著時間的推移，影響會逐漸消散，這是一個一階慣性環節的響應。整個過程可以抽象為李靖打在哪吒屁股上的巴掌在經過一階慣性環節之后，不同的輸入疊加，最終輸出的結果是哪吒現在屁股腫的程度。僅僅一巴掌，大概半小時就消下去了，但是由于李靖打的時間間隔縮小，當無窮小時就是連續的積分，最終的結果是得好幾天才能消腫。

所以通俗地講：卷積就是在輸入信號的每一個位置（每一巴掌）處疊加一個單位響應（半小時消腫），把每個位置得到的結果疊加就得到了輸出。對于離散系統來講，卷積的定義是

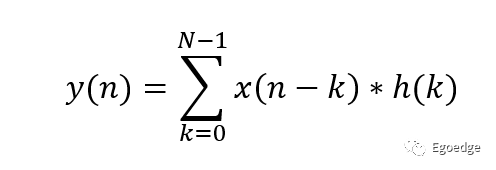
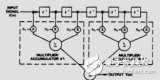
x(n-k)是依次的n個輸入，h(k)是每個輸入所對應的權值。在濾波的應用中，最簡單的就是移動平均數的方式，對相鄰的幾個歷史值做平均加權。這一節最開始放的示意圖是圖像處理中常用的一種移動平均的濾波方式。

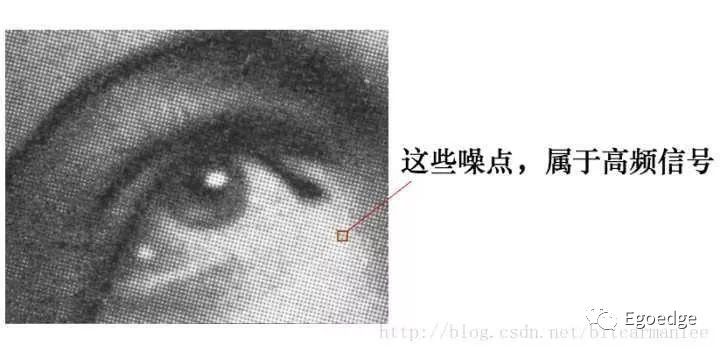
見上圖，圖中有很多噪點，這些噪點很尖銳，屬于高頻噪聲，將圖像提取出來，做成矩陣之后，就可以采用卷積的概念，把每一個點的輸出和周圍8個點做平均，于是得到如下的結果

FIR濾波器

在理解了卷積的概念之后，FIR濾波器就變得順理成章。把系統響應的函數換成我們所期望的函數，這樣卷積的過程就變成了FIR濾波器。我看到很多地方對濾波的定義是：用一個期望的頻率特征函數H(f)去乘以輸入信號頻率X(f)。對于這個解釋我理解了好久，為什么要用一個期望的函數去強行改變輸入頻率？但現在理解了之后，對這個解釋稍作修改之后應該會變得容易理解很多：用一個期望的頻率響應去乘以輸入信號，這就是濾波。

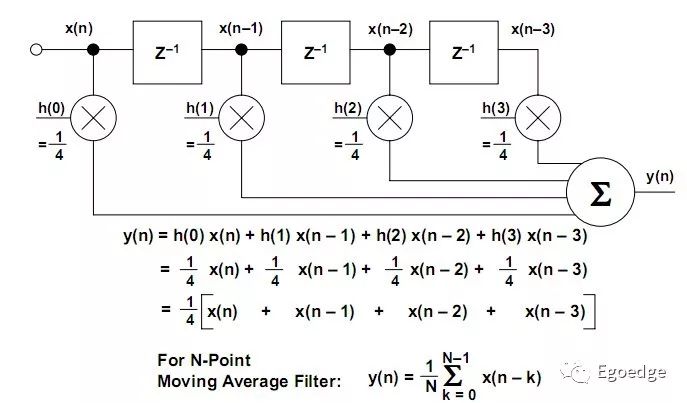
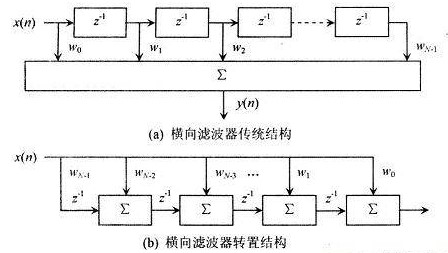
上圖是FIR的一個典型的結構，是一個簡單的四階移動平均的FIR濾波器。每次的輸出都是對4次歷史值的平均。下圖分別是經過11階平均和51階平均的效果。

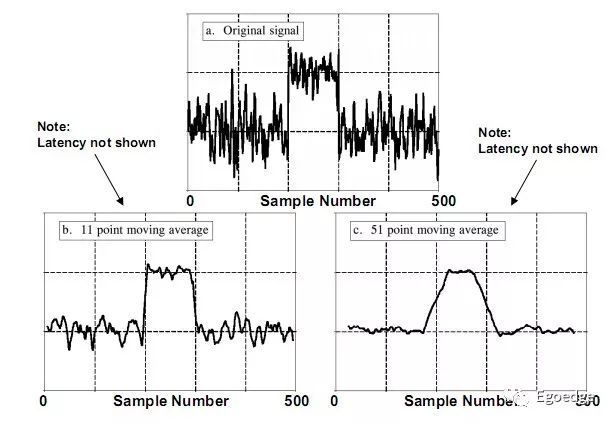
當我們把平均值的響應函數換成我們所期望的響應函數，這樣就變成了我們想要的濾波器。我們設計濾波器的過程就是選擇FIR中各階輸入的權重值的過程。

FIR濾波器和FFT

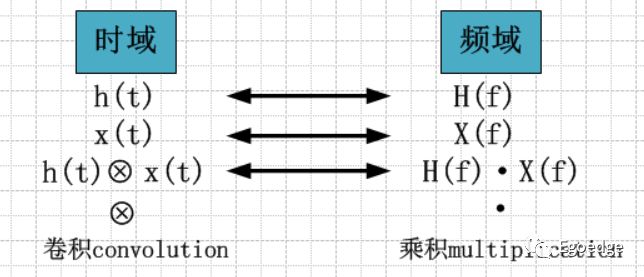
濾波就是用一個期望的頻率響應去乘以輸入信號的頻率，這個定義更明確一點來說是在頻域上對濾波概念的解釋，而在時域的解釋就是用我們所期望的響應函數h(f)做iFFT之后的時域函數H(t)和輸入信號X(t)做卷積。可以看到FIR濾波器其實是遵循的濾波在時域上的定義。

傅里葉前輩不僅給我們指出，所有的信號都可以被分解為若干正弦波的疊加，同時還給出了我們時域頻域相互變換的方法，其中有一條相當重要的結論就是：時域上的卷積等價于頻域上的乘積。因此對于FIR濾波器來講，我們只需要把輸入信號變換到頻域，再乘以我們期望的響應函數，再逆變換到時域，就得到了濾波后的結果。

FIR濾波器的設計

在有了FFT的工具之后，我們就可以很方便的進行FIR濾波器的設計。根據上面的說法，我們只需要給定所期望的特征函數h(f)，就可以得到結果，再逆變換回時域，算出不同tap的權值，就得到了時域上FIR的濾波器參數。

FIR濾波器的設計一般有窗函數法、頻率取樣法和優選法。窗函數法由于其簡單直觀，應用最多最廣泛。舉例說明窗函數法的設計應用。

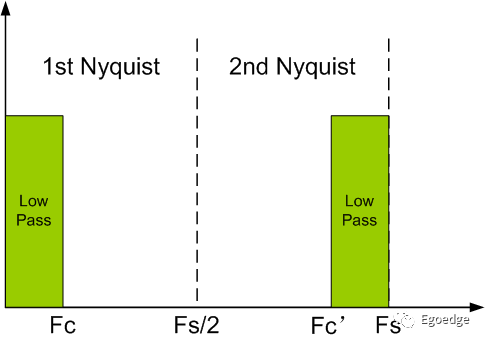
假設我們要設計一個低通濾波器，在頻譜上的表示如上圖，Fs是采樣率，在第一奈奎斯特區內是低通的特性。所謂窗函數法就是加一個濾波器的窗口，如上圖所示，對于低通的特性，理想效果是一個矩形窗，低于截止頻率通，高于截止頻率不通。

假設我們所要設計的濾波器為128階，截止頻率是Fc，在頻譜上的表示就是Nc=Fc*(Fs/128)，然后得到期望的特征函數

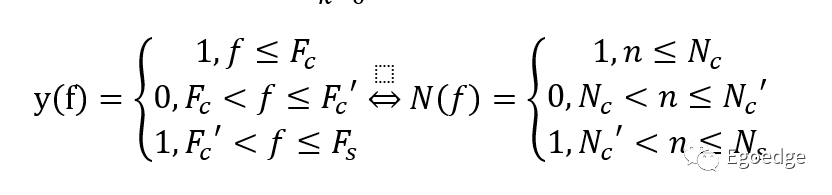
在頻域上，用這個特征函數乘以信號，就得到了輸出的結果。我們用一個0Hz~Fs的chirp信號輸入濾波器來測試，這個chirp信號的頻譜就是一個矩形，得到的結果見下圖

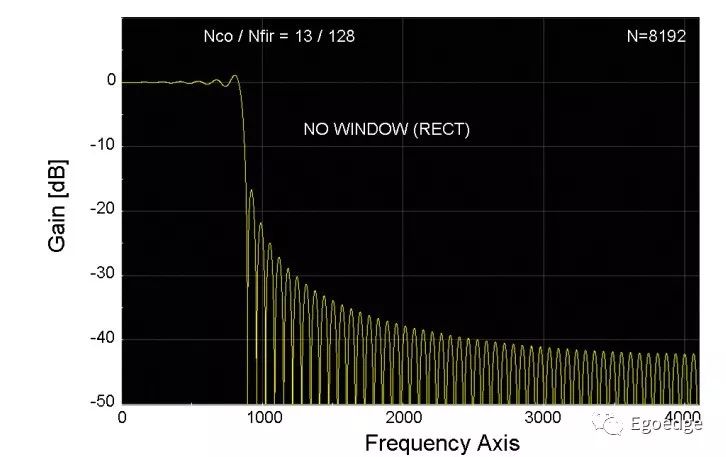
可以看到128階FIR濾波器的邊沿還是非常陡的，有很好的濾波性能，但旁瓣的抑制很差，這個就是FIR濾波器在頻譜上的泄露。泄露是由于FFT只能處理有限時間長度的時域信號，如果時域截取的數據不是信號周期的整數倍，就會存在泄露。由于矩形窗的邊沿過于陡，只有很小的概率正好截取到信號周期的整數倍，因此泄露很嚴重。可以通過選擇合適的窗函數，來減少頻譜上發生的泄露。一般常用的窗函數有矩形窗、漢寧窗和平頂窗，他們的特征如下圖所示

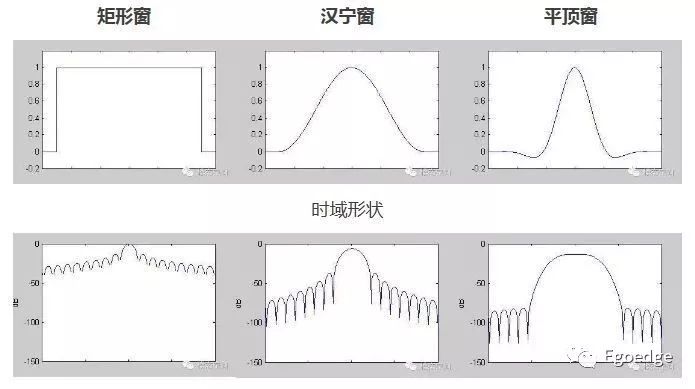
不同窗函數所對應的結果看下圖

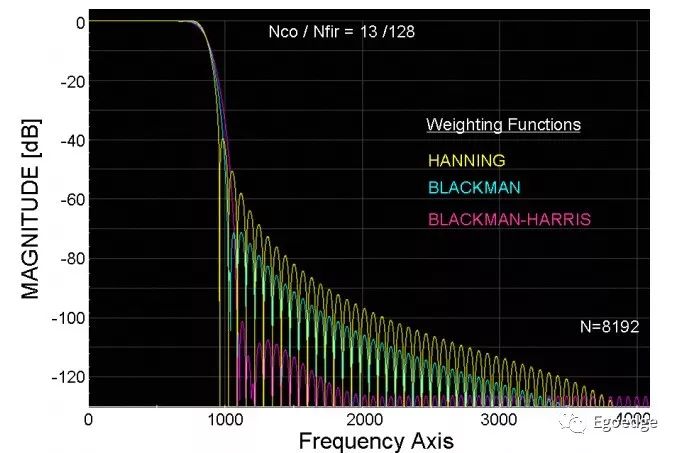
關于窗函數就不再介紹了，窗函數的選擇是FIR濾波器設計的重點，矩形窗的優點在于計算量小，其他的窗函數基本都是基于升余弦函數，漢寧窗屬于升余弦函數的一個特例。有興趣的大家自己可以去研究研究。

最后要說的一點是，FIR濾波器的階數越高，則邊沿越陡，運算量越大。