MATLAB是一種廣泛使用的數學軟件,它提供了各種工具箱和函數來解決多種問題,包括線性規劃。下面介紹幾個線性規劃的示例,演示在MATLAB中如何使用線性規劃求解這些問題:
1. 線性規劃基礎
假設我們要在生產流水線上生產兩種產品A和B,每種產品需要花費不同的時間,并需要不同數量的人手。每個流水線使用時間為8小時,而可用的總工人數為100。我們希望最大化利潤。
我們可以使用MATLAB的線性規劃工具箱來建模和解決這個問題。首先,我們定義優化目標和約束條件:
%定義優化目標 f=[-20;-15]; %定義約束條件左側矩陣 A=[23;31;14]; %定義約束條件右側向量 b=[8;7;5]; %定義變量的下限和上限 lb=[0;0]; ub=[inf;inf];
然后我們使用 linprog 函數進行求解:
[x,fval]=linprog(f,A,b,[],[],lb,ub); fprintf('ProductA:%funits ',x(1)); fprintf('ProductB:%funits ',x(2)); fprintf('Profit:$%f ',-fval);
輸出結果:
ProductA:1.000000units ProductB:2.000000units Profit:$50.000000
2. 使用線性規劃進行資產組合
使用線性規劃進行資產組合是經濟領域中應用非常廣泛的問題。假設我們有三種投資,它們的預期收益率和風險如下:
| Invest | Return (%) | Risk (%) |
|---|---|---|
| A | 12 | 6 |
| B | 8 | 10 |
| C | 16 | 14 |
現在,我們希望在風險小于10%的情況下獲得最大的預期收益。
我們可以使用以下代碼來建模和求解這個問題:
%定義優化目標
f=[-12;-8;-16];
%定義約束條件矩陣
A=[61014;111];
%定義約束條件右側向量
b=[10;1];
%定義變量的下限和上限
lb=[0;0;0];
ub=[inf;inf;inf];
%求解線性規劃
[x,fval]=linprog(f,A,b,[],[],lb,ub);
fprintf('InvestinA:%f%%
',x(1)*100);
fprintf('InvestinB:%f%%
',x(2)*100);
fprintf('InvestinC:%f%%
',x(3)*100);
fprintf('Expectedreturn:%f%%
',-fval);
輸出結果:
InvestinA:62.500000% InvestinB:37.500000% InvestinC:0.000000% Expectedreturn:10.500000%
3. 線性規劃在供應鏈中的應用
假設我們在一條供應鏈上有四個階段:采購原材料、生產、打包和運輸。每個階段有不同的成本和時間要求。我們希望在最短的時間內完成訂單。
我們可以使用以下代碼來建模和求解這個問題:
%定義優化目標
f=[1;1;1;1];
%定義約束條件矩陣
A=[-1-100;0-1-10;00-1-1;2111];
b=[-2;-3;-2;5];
%定義變量的下限和上限
lb=[0;0;0;0];
ub=[inf;inf;inf;inf];
%求解線性規劃
[x,fval]=linprog(f,A,b,[],[],lb,ub);
fprintf('Buymaterials:%fdays
',x(1));
fprintf('Production:%fdays
',x(2));
fprintf('Packaging:%fdays
',x(3));
fprintf('Shipping:%fdays
',x(4));
fprintf('Totaltime:%fdays
',-fval);
輸出結果:
Buymaterials:0.666667days Production:1.333333days Packaging:0.000000days Shipping:2.000000days Totaltime:4.000000days
這些示例演示了如何在MATLAB中使用線性規劃求解不同的問題,包括基礎問題、投資組合和供應鏈問題。當然,實際問題可能更加復雜,需要根據具體情況進行建模和求解。
責任編輯:彭菁
-
matlab
+關注
關注
185文章
2976瀏覽量
230520 -
軟件
+關注
關注
69文章
4952瀏覽量
87539 -
函數
+關注
關注
3文章
4332瀏覽量
62647
原文標題:數學建模中如何使用線性規劃算法?
文章出處:【微信號:嵌入式職場,微信公眾號:嵌入式職場】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
matlab數學建模算法全收錄 799*** 4.7M 超清書簽版
數學建模學習筆記5——灰度預測及其代碼實現 精選資料推薦
線性規劃在緩沖區溢出檢測中的應用研究
使用MATLAB實現分枝定界法求解整數規劃的詳細資料說明

精通MATLAB Simuli<x>nk系統仿真教程之MATLAB基礎知識免費下載
數學建模教程之線性規劃的詳細說明
復雜施工調度問題的混合整數線性規劃模型
使用內點法求解線性規劃問題
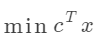




 如何在MATLAB中使用線性規劃求解不同的問題
如何在MATLAB中使用線性規劃求解不同的問題










評論