Test Card
射頻從業人員對于噪聲系數總是耳熟能詳,對其定義、級聯理論及對系統的影響,總是熟諳于心,但是對另外一個重要的概念——噪聲溫度可能相對生疏一些。其實,很多關于噪聲功率的理論推導都需要使用噪聲溫度。本文就給大家講一講關于噪聲溫度的內容。
定義在T0溫度
當討論某個參數時,往往繞不開定義,定義是非常重要的,不僅告訴人們這是什么,而且指明了成立的條件。所以,接下來還是先說說噪聲系數的定義。
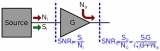
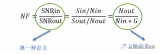
噪聲系數的定義有兩個版本,最早的版本是貝爾實驗室的Friis在1942年提出的,1949年正式出現在其公開發表的文獻“Noise Figures of Radio Receivers”中,這是從系統的角度首次定義了噪聲系數,Friis將輸入信噪比與輸出信噪比的比值定義為噪聲系數。
IRE在1960年發表的一篇關于噪聲測試標準的文章中,給出了另一個版本的噪聲系數定義。IRE與AIEE后來合并組成IEEE,所以又將其稱為IEEE版本的噪聲系數定義。大家現在從一些器件規格書上看到的噪聲系數都是IEEE版本的噪聲系數,由于指明了定義的條件,對端口數目也沒有限制,所以更具有普適性。
IEEE對噪聲系數的定義為:在T0 (290K) 溫度下,器件輸出的總噪聲功率與僅僅輸入噪聲功率引起的輸出噪聲功率的比值。
這個定義很拗口,不過本文要強調的是:噪聲系數是在T0溫度下定義的,不是其它溫度。所有器件、模塊的噪聲系數,都是在T0溫度下定義的。因此,誰的噪聲系數好,誰的噪聲系數差,才有統一的評判標準。
Te是等效輸入噪聲溫度
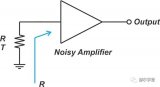
考慮圖1所示的低噪聲放大器,輸入端接匹配負載。假設其增益和噪聲因子分別為G和F,在T0溫度下,放大器在帶寬B內輸出的噪聲功率與輸入噪聲功率存在如下關系。
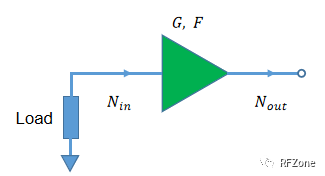
圖1. 端接負載的低噪聲放大器
Nout = Nin × G + Nadd
式中,Nadd為放大器自身產生的輸出噪聲功率,如果將其等效于輸入端,則可寫為
Nout = (Nin + Nadd,in) × G
任意電阻在溫度T、帶寬B內產生的噪聲功率為kBT,T就是電阻的噪聲溫度。那么在T0溫度下,電阻產生的噪聲功率為
Nin = kBT0
任何器件都有一個等效噪聲溫度,對于雙端口器件而言,理論上可以將噪聲溫度等效在輸入側,也可以等效在輸出側,但是當前基本都等效在輸入側。因此,放大器的等效噪聲溫度Te與Nadd,in存在如下關系
Nadd,in = kBTe
Te是輸入等效噪聲溫度,當根據器件的等效噪聲溫度計算輸出噪聲功率時,都要乘以器件本身的增益或損耗。
Nout = (kBT0 + kBTe) × G
Nout = kBT0 × (1 + Te/T0) × G
Nout = Nin × (1 + Te/T0) × G
進一步變換為
Nout / (Nin × G) = 1 + Te/T0
“=”左側就是IEEE給出的噪聲系數定義,因此
F = 1 + Te/T0
Te = (F - 1) × T0
這就是等效噪聲溫度與噪聲系數(線性值)之間的關系,二者都是在T0溫度下定義的,但是無論室溫是多少,上述關系都是成立的。
舉例:圖1所示的放大器增益為20dB,噪聲系數為2dB,計算300K室溫下,在1MHz噪聲帶寬內輸出的噪聲功率是多少?
噪聲系數的線性值為:1.59
等效噪聲溫度為:
Te = (F - 1) × T0 = 0.59×290=171.1 K
輸出噪聲功率為:
Nout = kBT0 × (Ta + Te)/T0 × G
(Ta + Te)/T0 = 1.62
則輸出功率寫成對數形式為
Nout(dBm) = -174dBm/Hz + 60dBHz + 20dB + 2.1dB = -91.9dBm
值得一提的是,噪聲系數的線性值通常稱為噪聲因子,而噪聲系數為噪聲因子的對數值。為了方便,文中統一稱為噪聲系數。
-
放大器
+關注
關注
143文章
13612瀏覽量
213708 -
電阻器
+關注
關注
21文章
3784瀏覽量
62192 -
低噪聲放大器
+關注
關注
6文章
248瀏覽量
31732
發布評論請先 登錄
相關推薦
計算ADC噪聲系數需知
噪聲系數的測量方法和公式

噪聲因子和噪聲系數
如何測試天線的噪聲溫度

噪聲系數測量方法和公式
現代無線電接收機的系統噪聲系數分析




 淺析噪聲系數與噪聲溫度
淺析噪聲系數與噪聲溫度
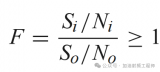










評論