兵(車)王問題的樣本數據集包含六個維度,六個維度代表三個棋子在棋盤中的位置。總樣本數為28056個,其中,正樣本(和棋)數量為2796個,負樣本(白方勝)數量為25260個。
一、數據預處理
28056個樣本中的隨機5000個樣本被用于樣本訓練(即此5000個樣本為訓練樣本),其余樣本被用于測試(即其余樣本為測試樣本)。
然后,求出訓練樣本每個維度的均值和方差,并將訓練樣本和測試樣本歸一化,各個維度歸一化后的值與原值的等量關系為:
newX=(X-meanX)/std(X) 樣本歸一化可將數據集的每個維度的值限定于一個固定范圍內,從而減少因各個維度取值范圍的差異而導致的訓練誤差。
二、設置支持向量機的參數
(1)-s “-s”表示支持向量機不同的形式。因為兵(車)王問題屬于二分類問題,且最優化問題的目標函數為1/2||ω||2+C∑δi(式①),所以-s的取值為0。-s的數值處于1~4所分別對應支持向量機的形式可查詢LIBSVM工具包或其他資料。
圖片來源:中國慕課大學《機器學習概論》
(2)-t “-t”參數確定支持向量機的核函數K(X1,X2)。LIBSVM工具包支持的核函數包括:LInear(線性內核,-t=0)、Ploy(多項式核,-t=1)、Rbf(高斯徑向基函數核,-t=2)、Tanh(sigmoid核,-t=3)、自定義核(,-t=4)。
圖片來源:中國慕課大學《機器學習概論》
1)線性內核 線性內核的表達式為K(x,y)=xTy。線性內核具有理論意義,但因為使用線性內核求解支持向量機與不使用核函數求解支持向量機無差別(個人理解:因為線性內核的核函數都可以求出其對應的φ(x),所以不使用核函數也可以求解),所以線性內核不具有實際使用價值。
2)多項式核 多項式核的表達式為K(x,y)=(xTy+1)d。多項式核是維度可以調節的函數,表達式中的d越大,對應的φ(x)維度越高。
3)高斯徑向基函數核 高斯徑向基函數核的表達式為K(x,y)=e-(||x-y||2)/σ2。表達式中的σ是人為設置的超參數,該函數的維度是無限的。課程中建議:若處理實際問題中不知道選擇哪種核函數,則首選該函數。
4)sigmoid核 sigmoid核的表達式為K(x,y)=tanh(βxTy+b),其中,tanh(x)=(ex-e-x)/(ex+e-x)。表達式中β、b均是人為設置的超參數,該函數的維度是無限的。
5)自定義核 因為支持向量機通過求解其優化問題的對偶問題: 最大化:θ(α,β)=∑αi-1/2∑∑yiyjαiαjφ(Xi)Tφ(Xj);
限制條件:
(1)0≤αi≤C,i=1~N;
(2)∑αiyi=0,i=1~N。(式②) 的αi求解可用于樣本分類的超平面,所以若開發人員已知圖一核函數矩陣的具體形式,則其可通過輸入該核函數矩陣求解用于樣本分類的超平面(個人理解:將核函數矩陣中各個核函數值替換φ(Xi)Tφ(Xj)即可求解超平面)。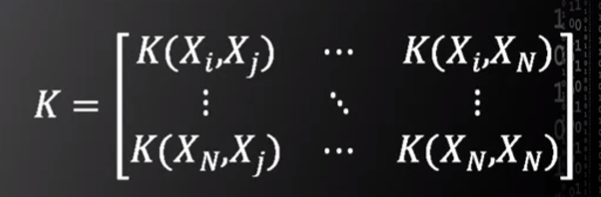
圖片來源:中國慕課大學《機器學習概論》
(3)-c “-c”代表式①和式②中C的值(式①和式②中C為同一參數)。
(4)-g(gamma) “-g”所代表的值與所選擇的核函數有關,例如:若選擇Rbf為核函數,則-g代表1/σ2。
審核編輯:劉清
-
向量機
+關注
關注
0文章
166瀏覽量
20888
原文標題:機器學習相關介紹(16)——支持向量機(兵(車)王問題程序設計)
文章出處:【微信號:行業學習與研究,微信公眾號:行業學習與研究】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦

基于改進支持向量機的貨幣識別研究
基于支持向量機(SVM)的工業過程辨識
單片機教程之51單片機C語言程序設計教程(王云)資料合集
什么是支持向量機 什么是支持向量




 支持向量機(兵(車)王問題程序設計)
支持向量機(兵(車)王問題程序設計)











評論