在本節中,我們將展示如何使用我們在上一節中介紹的 GP 先驗執行后驗推理和進行預測。我們將從回歸開始,我們可以在其中以封閉形式執行推理。這是一個“簡而言之 GP”部分,可在實踐中快速啟動和運行高斯過程。我們將從頭開始編寫所有基本操作的代碼,然后介紹 GPyTorch,這將使使用最先進的高斯過程以及與深度神經網絡的集成更加方便。我們將在下一節中深入探討這些更高級的主題。在該部分中,我們還將考慮需要近似推理的設置——分類、點過程或任何非高斯似然。
18.3.1。回歸的后驗推理
觀察模型與我們想要學習的功能相關聯, f(x), 根據我們的觀察y(x), 都由一些輸入索引x. 在分類上,x可以是圖像的像素,并且y可能是關聯的類標簽。在回歸中, y通常表示連續輸出,例如地表溫度、海平面、CO2濃度等
在回歸中,我們通常假設輸出是由潛在的無噪聲函數給出的f(x)加上 iid 高斯噪聲 ?(x):
(18.3.1)y(x)=f(x)+?(x),
和?(x)~N(0,σ2). 讓 y=y(X)=(y(x1),…,y(xn))?是我們訓練觀察的向量,并且 f=(f(x1),…,f(xn))?是潛在無噪聲函數值的向量,在訓練輸入中查詢 X=x1,…,xn.
我們假設f(x)~GP(m,k),這意味著任何函數值的集合f具有聯合多元高斯分布,均值向量 μi=m(xi)和協方差矩陣 Kij=k(xi,xj). RBF核 k(xi,xj)=a2exp?(?12?2||xi?xj||2) 將是協方差函數的標準選擇。為了符號簡單起見,我們將假設均值函數m(x)=0; 我們的推導可以在以后很容易地推廣。
假設我們想對一組輸入進行預測
(18.3.2)X?=x?1,x?2,…,x?m.
那么我們想要找到x2和 p(f?|y,X). 在回歸設置中,我們可以在找到聯合分布后,使用高斯恒等式方便地找到這個分布f?=f(X?) 和y.
如果我們在訓練輸入處評估等式(18.3.1)X, 我們有 y=f+?. 根據高斯過程的定義(見上一節), f~N(0,K(X,X))在哪里K(X,X)是一個 n×n通過在所有可能的輸入對上評估我們的協方差函數(又名kernel )形成的矩陣xi,xj∈X. ?只是一個由 iid 樣本組成的向量N(0,σ2)從而有分布 N(0,σ2I).y因此是兩個獨立的多元高斯變量的總和,因此具有分布N(0,K(X,X)+σ2I). 也可以證明 cov(f?,y)=cov(y,f?)?=K(X?,X) 在哪里K(X?,X)是一個m×n通過評估所有對測試和訓練輸入的內核形成的矩陣。
(18.3.3)[yf?]~N(0,A=[K(X,X)+σ2IK(X,X?)K(X?,X)K(X?,X?)])
然后我們可以使用標準高斯恒等式從聯合分布中找到條件分布(例如,參見 Bishop 第 2 章), f?|y,X,X?~N(m?,S?), 在哪里m?=K(X?,X)[K(X,X)+σ2I]?1y, 和 S=K(X?,X?)?K(X?,X)[K(X,X)+σ2I]?1K(X,X?).
通常,我們不需要使用完整的預測協方差矩陣S, 而不是使用對角線S對于每個預測的不確定性。通常出于這個原因,我們為單個測試點編寫預測分布x?,而不是測試點的集合。
核矩陣有參數θ我們也希望估計,例如振幅a和長度尺度?上面的 RBF 內核。為了這些目的,我們使用邊際似然,p(y|θ,X),我們已經在計算邊際分布以找到聯合分布時得出y,f?. 正如我們將看到的,邊際似然劃分為模型擬合和模型復雜性項,并自動編碼用于學習超參數的奧卡姆剃刀概念。有關完整討論,請參閱 MacKay Ch。28 (MacKay 和 Mac Kay,2003 年),以及 Rasmussen 和 Williams Ch。5 (拉斯穆森和威廉姆斯,2006 年)。
import math import os import gpytorch import matplotlib.pyplot as plt import numpy as np import torch from scipy import optimize from scipy.spatial import distance_matrix from d2l import torch as d2l d2l.set_figsize()
18.3.2。在 GP 回歸中進行預測和學習內核超參數的方程式
我們在這里列出了您將用于學習超參數和在高斯過程回歸中進行預測的方程式。同樣,我們假設一個回歸目標向量y, 由輸入索引 X={x1,…,xn},我們希望在測試輸入中做出預測x?. 我們假設具有方差的 iid 加性零均值高斯噪聲σ2. 我們先使用高斯過程 f(x)~GP(m,k)對于潛在的無噪聲函數,具有均值函數m和核函數k. 內核本身有參數θ我們想學習。例如,如果我們使用 RBF 內核, k(xi,xj)=a2exp?(?12?2||x?x′||2), 我們想學習θ={a2,?2}. 讓K(X,X) 代表一個n×n對應于為所有可能的對評估內核的矩陣n培訓投入。讓 K(x?,X)代表一個1×n通過評估形成的向量k(x?,xi),i=1,…,n. 讓μ是通過計算均值函數形成的均值向量m(x)在每個訓練點x.
通常在處理高斯過程時,我們遵循一個兩步過程。1.學習內核超參數θ^通過最大化這些超參數的邊際似然。2.使用預測均值作為點預測器,2倍預測標準差形成95%可信集,以這些學習到的超參數為條件θ^.
對數邊際似然只是一個對數高斯密度,其形式為:
(18.3.4)log?p(y|θ,X)=?12y?[Kθ(X,X)+σ2I]?1y?12log?|Kθ(X,X)|+c
預測分布具有以下形式:
(18.3.5)p(y?|x?,y,θ)=N(a?,v?)
(18.3.6)a?=kθ(x?,X)[Kθ(X,X)+σ2I]?1(y?μ)+μ
(18.3.7)v?=kθ(x?,x?)?Kθ(x?,X)[Kθ(X,X)+σ2I]?1kθ(X,x?)
18.3.3。解釋學習和預測方程
關于高斯過程的預測分布,有一些關鍵點需要注意:
盡管模型類具有靈活性,但可以 對封閉形式的 GP 回歸進行精確的貝葉斯推理。除了學習內核超參數外,沒有任何訓練。我們可以準確地寫下我們想要用來進行預測的方程式。高斯過程在這方面相對特殊,這極大地促進了它們的便利性、多功能性和持續流行。
預測均值a?是訓練目標的線性組合y, 由內核加權 kθ(x?,X)[Kθ(X,X)+σ2I]?1. 正如我們將看到的,內核(及其超參數)因此在模型的泛化特性中起著至關重要的作用。
預測均值明確取決于目標值 y但預測方差沒有。預測不確定性反而隨著測試輸入而增長x? 遠離目標位置X,由內核函數控制。然而,不確定性將隱含地取決于目標的價值y通過內核超參數θ,這是從數據中學到的。
邊際似然劃分為模型擬合和模型復雜性(對數行列式)項。邊際似然傾向于選擇提供與數據仍然一致的最簡單擬合的超參數。
關鍵的計算瓶頸來自解決線性系統和計算對數行列式n×n對稱正定矩陣K(X,X)為了n訓練點。天真地,這些操作每個都會招致O(n3) 計算,以及O(n2)核(協方差)矩陣的每個條目的存儲,通常從 Cholesky 分解開始。從歷史上看,這些瓶頸將 GP 限制在訓練點少于 10,000 的問題上,并給 GP 帶來了近十年來不準確的“速度慢”的名聲。在高級主題中,我們將討論如何將 GP 擴展到具有數百萬個點的問題。
對于核函數的流行選擇,K(X,X)通常接近奇異,這可能會在執行 Cholesky 分解或其他旨在求解線性系統的操作時導致數值問題。幸運的是,在回歸中我們經常使用 Kθ(X,X)+σ2I,使得噪聲方差 σ2被添加到對角線K(X,X), 顯著改善其條件。如果噪聲方差很小,或者我們正在進行無噪聲回歸,通常的做法是在對角線上添加少量“抖動”,數量級為 10?6, 改善調理。
18.3.4。從零開始的工作示例
讓我們創建一些回歸數據,然后用 GP 擬合數據,從頭開始實施每一步。我們將從中抽樣數據
(18.3.8)y(x)=sin?(x)+12sin?(4x)+?,
和?~N(0,σ2). 我們希望找到的無噪聲函數是 f(x)=sin?(x)+12sin?(4x). 我們將從使用噪聲標準偏差開始σ=0.25.
def data_maker1(x, sig): return np.sin(x) + 0.5 * np.sin(4 * x) + np.random.randn(x.shape[0]) * sig sig = 0.25 train_x, test_x = np.linspace(0, 5, 50), np.linspace(0, 5, 500) train_y, test_y = data_maker1(train_x, sig=sig), data_maker1(test_x, sig=0.) d2l.plt.scatter(train_x, train_y) d2l.plt.plot(test_x, test_y) d2l.plt.xlabel("x", fontsize=20) d2l.plt.ylabel("Observations y", fontsize=20) d2l.plt.show()
在這里,我們將嘈雜的觀察結果視為圓圈,將我們希望找到的藍色無噪聲函數視為圓圈。
現在,讓我們在潛在無噪聲函數之前指定一個 GP, f(x)~GP(m,k). 我們將使用均值函數 m(x)=0和 RBF 協方差函數(核)
(18.3.9)k(xi,xj)=a2exp?(?12?2||x?x′||2).
mean = np.zeros(test_x.shape[0]) cov = d2l.rbfkernel(test_x, test_x, ls=0.2)
我們從 0.2 的長度尺度開始。在我們擬合數據之前,重要的是要考慮我們是否指定了合理的先驗。讓我們想象一下這個先驗的一些樣本函數,以及 95% 的可信集(我們相信真正的函數有 95% 的可能性在這個區域內)。
prior_samples = np.random.multivariate_normal(mean=mean, cov=cov, size=5)
d2l.plt.plot(test_x, prior_samples.T, color='black', alpha=0.5)
d2l.plt.plot(test_x, mean, linewidth=2.)
d2l.plt.fill_between(test_x, mean - 2 * np.diag(cov), mean + 2 * np.diag(cov),
alpha=0.25)
d2l.plt.show()
這些樣本看起來合理嗎?函數的高級屬性是否與我們嘗試建模的數據類型一致?
現在讓我們在任意測試點形成后驗預測分布的均值和方差x?.
(18.3.10)fˉ?=K(x,x?)T(K(x,x)+σ2I)?1y
(18.3.11)V(f?)=K(x?,x?)?K(x,x?)T(K(x,x)+σ2I)?1K(x,x?)
在我們做出預測之前,我們應該學習我們的內核超參數 θ和噪聲方差σ2. 讓我們將長度尺度初始化為 0.75,因為與我們正在擬合的數據相比,我們之前的函數看起來變化太快了。我們還將猜測噪聲標準偏差σ0.75。
為了學習這些參數,我們將最大化這些參數的邊際似然。
(18.3.12)log?p(y|X)=log?∫p(y|f,X)p(f|X)df
(18.3.13)log?p(y|X)=?12yT(K(x,x)+σ2I)?1y?12log?|K(x,x)+σ2I|?n2log?2π
也許我們之前的功能變化太快了。我們假設長度尺度為 0.4。我們還將猜測噪聲標準偏差為 0.75。這些只是超參數初始化——我們將從邊際似然中學習這些參數。
ell_est = 0.4 post_sig_est = 0.5 def neg_MLL(pars): K = d2l.rbfkernel(train_x, train_x, ls=pars[0]) kernel_term = -0.5 * train_y @ np.linalg.inv(K + pars[1] ** 2 * np.eye(train_x.shape[0])) @ train_y logdet = -0.5 * np.log(np.linalg.det(K + pars[1] ** 2 * np.eye(train_x.shape[0]))) const = -train_x.shape[0] / 2. * np.log(2 * np.pi) return -(kernel_term + logdet + const) learned_hypers = optimize.minimize(neg_MLL, x0=np.array([ell_est,post_sig_est]), bounds=((0.01, 10.), (0.01, 10.))) ell = learned_hypers.x[0] post_sig_est = learned_hypers.x[1]
在本例中,我們學習了 0.299 的長度尺度和 0.24 的噪聲標準差。請注意,學習到的噪聲非常接近真實噪聲,這有助于表明我們的 GP 非常明確地解決了這個問題。
一般來說,仔細考慮選擇內核和初始化超參數是至關重要的。雖然邊際似然優化對初始化來說相對穩健,但它也不能避免糟糕的初始化。嘗試使用各種初始化運行上面的腳本,看看你發現了什么結果。
現在,讓我們用這些學習到的超級計算機進行預測。
K_x_xstar = d2l.rbfkernel(train_x, test_x, ls=ell)
K_x_x = d2l.rbfkernel(train_x, train_x, ls=ell)
K_xstar_xstar = d2l.rbfkernel(test_x, test_x, ls=ell)
post_mean = K_x_xstar.T @ np.linalg.inv((K_x_x +
post_sig_est ** 2 * np.eye(train_x.shape[0]))) @ train_y
post_cov = K_xstar_xstar - K_x_xstar.T @ np.linalg.inv((K_x_x +
post_sig_est ** 2 * np.eye(train_x.shape[0]))) @ K_x_xstar
lw_bd = post_mean - 2 * np.sqrt(np.diag(post_cov))
up_bd = post_mean + 2 * np.sqrt(np.diag(post_cov))
d2l.plt.scatter(train_x, train_y)
d2l.plt.plot(test_x, test_y, linewidth=2.)
d2l.plt.plot(test_x, post_mean, linewidth=2.)
d2l.plt.fill_between(test_x, lw_bd, up_bd, alpha=0.25)
d2l.plt.legend(['Observed Data', 'True Function', 'Predictive Mean', '95% Set on True Func'])
d2l.plt.show()
我們看到橙色的后驗均值幾乎完全匹配真正的無噪聲函數!請注意,我們顯示的 95% 可信集是針對無潛在噪聲(真實)函數的,而不是數據點。我們看到這個可信集完全包含了真實的功能,并且看起來并不過分寬泛或狹窄。我們不希望也不期望它包含數據點。如果我們希望有一個可靠的觀察集,我們應該計算
lw_bd_observed = post_mean - 2 * np.sqrt(np.diag(post_cov) + post_sig_est ** 2) up_bd_observed = post_mean + 2 * np.sqrt(np.diag(post_cov) + post_sig_est ** 2)
不確定性有兩個來源,認知不確定性,代表可減少的不確定性,以及任意或不可減少的 不確定性。這里的認知不確定性表示無噪聲函數真實值的不確定性。隨著我們遠離數據點,這種不確定性應該會增加,因為遠離數據有更多種類的函數值與我們的數據一致。隨著我們觀察到越來越多的數據,我們對真實函數的信念變得更加自信,認知不確定性消失。這種情況下的任意 不確定性是觀察噪聲,因為數據是通過這種噪聲提供給我們的,并且無法減少。
數據中的認知不確定性由潛在無噪聲函數 np.diag(post_cov) 的方差捕獲。任意不 確定性由噪聲方差 post_sig_est**2 捕獲。
不幸的是,人們常常不關心他們如何表示不確定性,許多論文顯示的誤差條完全未定義,不清楚我們是在可視化認知不確定性還是任意不確定性或兩者兼而有之,并且將噪聲方差與噪聲標準差混淆,標準差與標準誤差、可信集的置信區間等。如果不明確不確定性代表什么,它本質上是沒有意義的。
本著密切關注我們的不確定性代表什么的精神,重要的是要注意我們對無噪聲函數的方差估計取平方根的 兩倍。由于我們的預測分布是高斯分布,這個數量使我們能夠形成一個 95% 的可信集,代表我們對 95% 可能包含基本事實函數的區間的信念。噪聲 方差存在于完全不同的尺度上,并且更難解釋。
最后,讓我們來看看20個后驗樣本。這些樣本告訴我們我們認為哪些類型的函數可能適合我們的數據,這是后驗的。
post_samples = np.random.multivariate_normal(post_mean, post_cov, size=20) d2l.plt.scatter(train_x, train_y) d2l.plt.plot(test_x, test_y, linewidth=2.) d2l.plt.plot(test_x, post_mean, linewidth=2.) d2l.plt.plot(test_x, post_samples.T, color='gray', alpha=0.25) d2l.plt.fill_between(test_x, lw_bd, up_bd, alpha=0.25) plt.legend(['Observed Data', 'True Function', 'Predictive Mean', 'Posterior Samples']) d2l.plt.show()
在基本回歸應用中,最常見的做法是分別使用后驗預測均值和標準差作為不確定性的點預測器和度量。在更高級的應用程序中,例如使用蒙特卡洛采集函數的貝葉斯優化或基于模型的 RL 的高斯過程,通常需要采用后驗樣本。然而,即使在基本應用程序中沒有嚴格要求,這些樣本也能讓我們更直觀地了解我們對數據的擬合程度,并且通常有助于將其包含在可視化中。
18.3.5。使用 GPyTorch 讓生活更輕松
正如我們所見,完全從頭開始實現基本的高斯過程回歸實際上非常容易。然而,一旦我們想要探索各種內核選擇,考慮近似推理(這甚至是分類所必需的),將 GP 與神經網絡相結合,甚至擁有大于約 10,000 個點的數據集,那么從頭開始的實現就變成了笨重和麻煩。一些最有效的可擴展 GP 推理方法,例如 SKI(也稱為 KISS-GP),可能需要數百行代碼來實現高級數值線性代數例程。
在這些情況下,GPyTorch庫將使我們的生活變得更加輕松。我們將在未來關于高斯過程數值和高級方法的筆記本中更多地討論 GPyTorch。GPyTorch 庫包含 許多示例。為了感受這個包,我們將通過簡單的回歸示例,展示如何使用 GPyTorch 對其進行調整以重現我們的上述結果。這看起來像是簡單地重現上面的基本回歸的大量代碼,從某種意義上說,它確實如此。但是我們可以立即使用各種內核、可擴展推理技術和近似推理,只需從下面更改幾行代碼,而不是編寫可能有數千行的新代碼。
# First let's convert our data into tensors for use with PyTorch
train_x = torch.tensor(train_x)
train_y = torch.tensor(train_y)
test_y = torch.tensor(test_y)
# We are using exact GP inference with a zero mean and RBF kernel
class ExactGPModel(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood):
super(ExactGPModel, self).__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ZeroMean()
self.covar_module = gpytorch.kernels.ScaleKernel(
gpytorch.kernels.RBFKernel())
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
此代碼塊將數據置于 GPyTorch 的正確格式中,并指定我們正在使用精確推理,以及我們要使用的均值函數(零)和核函數(RBF)。我們可以很容易地使用任何其他內核,例如,通過調用 gpytorch.kernels.matern_kernel() 或 gpyotrch.kernels.spectral_mixture_kernel()。到目前為止,我們只討論了精確推理,其中可以在不進行任何近似的情況下推斷出預測分布。對于高斯過程,我們只有在具有高斯似然時才能進行精確推理;更具體地說,當我們假設我們的觀察結果是由高斯過程和高斯噪聲表示的無噪聲函數生成的。在未來的筆記本中,我們將考慮其他設置,例如分類,我們無法做出這些假設。
# Initialize Gaussian likelihood likelihood = gpytorch.likelihoods.GaussianLikelihood() model = ExactGPModel(train_x, train_y, likelihood) training_iter = 50 # Find optimal model hyperparameters model.train() likelihood.train() # Use the adam optimizer, includes GaussianLikelihood parameters optimizer = torch.optim.Adam(model.parameters(), lr=0.1) # Set our loss as the negative log GP marginal likelihood mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
在這里,我們明確指定我們想要使用的可能性(高斯),我們將用于訓練內核超參數的目標(這里是邊際可能性),以及我們想要用于優化該目標的過程(在本例中,Adam ). 我們注意到,雖然我們使用的是“隨機”優化器 Adam,但在本例中,它是全批次 Adam。因為邊際似然不會分解數據實例,所以我們不能對“小批量”數據使用優化器并保證收斂。GPyTorch 也支持其他優化器,例如 L-BFGS。與標準深度學習不同,做好邊際似然優化工作與良好的泛化密切相關,這通常使我們傾向于使用像 L-BFGS 這樣強大的優化器,前提是它們的成本并不高得令人望而卻步。
for i in range(training_iter):
# Zero gradients from previous iteration
optimizer.zero_grad()
# Output from model
output = model(train_x)
# Calc loss and backprop gradients
loss = -mll(output, train_y)
loss.backward()
if i % 10 == 0:
print(f'Iter {i+1:d}/{training_iter:d} - Loss: {loss.item():.3f} '
f'squared lengthscale: '
f'{model.covar_module.base_kernel.lengthscale.item():.3f} '
f'noise variance: {model.likelihood.noise.item():.3f}')
optimizer.step()
Iter 1/50 - Loss: 0.973 squared lengthscale: 0.693 noise variance: 0.693 Iter 11/50 - Loss: 0.684 squared lengthscale: 0.511 noise variance: 0.313 Iter 21/50 - Loss: 0.422 squared lengthscale: 0.533 noise variance: 0.128 Iter 31/50 - Loss: 0.304 squared lengthscale: 0.535 noise variance: 0.056 Iter 41/50 - Loss: 0.320 squared lengthscale: 0.522 noise variance: 0.040
在這里,我們實際運行優化程序,每 10 次迭代輸出一次損失值。
# Get into evaluation (predictive posterior) mode test_x = torch.tensor(test_x) model.eval() likelihood.eval() observed_pred = likelihood(model(test_x))
上面的代碼塊使我們能夠對我們的測試輸入進行預測。
with torch.no_grad(): # Initialize plot f, ax = d2l.plt.subplots(1, 1, figsize=(4, 3)) # Get upper and lower bounds for 95% credible set (in this case, in # observation space) lower, upper = observed_pred.confidence_region() ax.scatter(train_x.numpy(), train_y.numpy()) ax.plot(test_x.numpy(), test_y.numpy(), linewidth=2.) ax.plot(test_x.numpy(), observed_pred.mean.numpy(), linewidth=2.) ax.fill_between(test_x.numpy(), lower.numpy(), upper.numpy(), alpha=0.25) ax.set_ylim([-1.5, 1.5]) ax.legend(['True Function', 'Predictive Mean', 'Observed Data', '95% Credible Set'])
最后,我們繪制擬合圖。
我們看到擬合幾乎相同。需要注意的幾件事:GPyTorch 正在處理平方長度尺度和觀察噪聲。例如,我們在 for scratch 代碼中學習到的噪聲標準差約為 0.283。GPyTorch 找到的噪聲方差是 0.81≈0.2832. 在 GPyTorch 圖中,我們還展示了觀察空間中的可信集而不是潛在函數空間,以證明它們確實覆蓋了觀察到的數據點。
18.3.6。概括
我們可以將高斯過程先驗與數據結合起來形成后驗,我們用它來進行預測。我們還可以形成邊際似然,這對于核超參數的自動學習很有用,核超參數控制高斯過程的變化率等屬性。為回歸形成后驗和學習內核超參數的機制很簡單,涉及大約十幾行代碼。對于任何想要快速“啟動并運行”高斯過程的讀者來說,這個筆記本都是一個很好的參考。我們還介紹了 GPyTorch 庫。盡管用于基本回歸的 GPyTorch 代碼相對較長,但可以針對其他內核函數或我們將在以后的筆記本中討論的更高級功能(例如可擴展推理或用于分類的非高斯似然)進行簡單修改。
18.3.7。練習
我們強調了學習內核超參數的重要性,以及超參數和內核對高斯過程泛化特性的影響。嘗試跳過我們學習 hypers 的步驟,而是猜測各種長度尺度和噪聲方差,并檢查它們對預測的影響。當你使用大長度尺度時會發生什么?一個小的長度尺度?噪聲方差大?噪聲方差小?
我們已經說過邊際似然不是凸目標,但是可以在 GP 回歸中可靠地估計長度尺度和噪聲方差等超參數。這通常是正確的——事實上,邊際似然在學習長度尺度超參數方面比空間統計中的傳統方法要好得多,后者涉及擬合經驗自相關函數(“協方差圖”)。可以說,至少在最近關于可擴展推理的工作之前,機器學習對高斯過程研究的最大貢獻是為超參數學習引入了邊際似然。
然而,即使這些參數的不同配對也為許多數據集提供了可解釋的不同合理解釋,從而導致我們目標中的局部最優。如果我們使用大長度尺度,那么我們假設真正的基礎函數正在緩慢變化。如果觀察到的數據變化很大,那么我們唯一可以合理地擁有大長度尺度的就是大的噪聲方差。另一方面,如果我們使用較小的長度尺度,我們的擬合將對數據的變化非常敏感,幾乎沒有空間來解釋噪聲變化(任意不確定性)。
嘗試看看您是否可以找到這些局部最優值:使用具有大噪聲的非常大的長度尺度和具有小噪聲的小長度尺度進行初始化。你會收斂到不同的解決方案嗎?
我們已經說過,貝葉斯方法的一個基本優勢是自然地表示認知不確定性。在上面的例子中,我們無法完全看到認知不確定性的影響。嘗試使用 進行預測。當您的預測超出數據范圍時,95% 的可信集會發生什么變化?它是否涵蓋了該區間內的真實函數?如果你只想象那個區域的任意不確定性,會發生什么?test_x = np.linspace(0, 10, 1000)
嘗試運行上述示例,但使用 10,000、20,000 和 40,000 個訓練點,并測量運行時間。培訓時間如何安排?或者,運行時間如何隨測試點的數量變化?預測均值和預測方差是否不同?通過從理論上計算出訓練和測試的時間復雜度,以及使用不同數量的點運行上面的代碼來回答這個問題。
嘗試使用不同的協方差函數運行 GPyTorch 示例,例如 Matern 內核。結果如何變化?在 GPyTorch 庫中找到的光譜混合內核怎么樣?有些比其他更容易訓練邊際可能性嗎?一些對于長期預測和短期預測更有價值嗎?
在我們的 GPyTorch 示例中,我們繪制了包括觀察噪聲在內的預測分布,而在我們的“從頭開始”示例中,我們僅包括認知不確定性。重做 GPyTorch 示例,但這次只繪制認知不確定性,并與從頭開始的結果進行比較。預測分布現在看起來一樣嗎?(他們應該。)
Discussions
-
GP
+關注
關注
0文章
31瀏覽量
23613 -
pytorch
+關注
關注
2文章
808瀏覽量
13574
發布評論請先 登錄
相關推薦
高斯過程回歸GPR和多任務高斯過程MTGP
怎樣使用PyTorch Hub去加載YOLOv5模型
基于狄利克雷過程的可擴展高斯混合模型

什么是高斯過程 神經網絡高斯過程解析
PyTorch教程-18.1. 高斯過程簡介
PyTorch教程-18.2. 高斯過程先驗
Pytorch Hub兩行代碼搞定YOLOv5推理

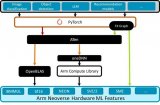
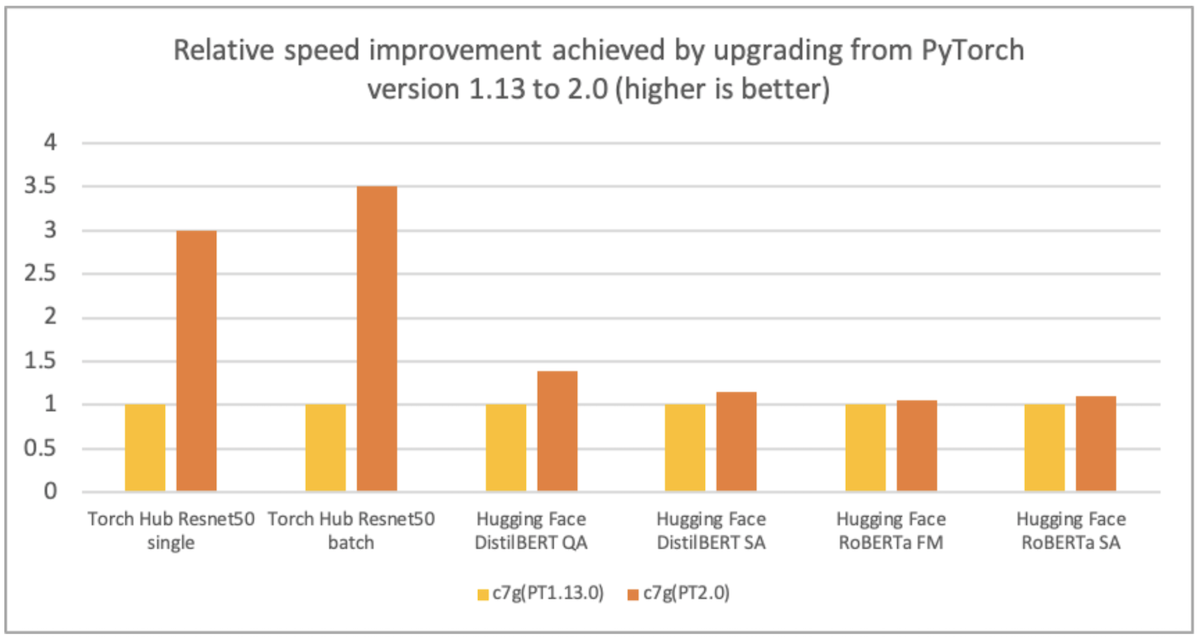
利用Arm Kleidi技術實現PyTorch優化



















評論