我們現(xiàn)在準(zhǔn)備好通過線性回歸的全功能實現(xiàn)來工作。在本節(jié)中,我們將從頭開始實現(xiàn)整個方法,包括(i)模型;(ii) 損失函數(shù);(iii) 小批量隨機(jī)梯度下降優(yōu)化器;(iv) 將所有這些部分拼接在一起的訓(xùn)練功能。最后,我們將運行3.3 節(jié)中的合成數(shù)據(jù)生成器 并將我們的模型應(yīng)用于生成的數(shù)據(jù)集。雖然現(xiàn)代深度學(xué)習(xí)框架幾乎可以自動執(zhí)行所有這些工作,但從頭開始實施是確保您真正了解自己在做什么的唯一方法。此外,當(dāng)需要自定義模型、定義我們自己的層或損失函數(shù)時,了解引擎蓋下的工作原理將很方便。在本節(jié)中,我們將僅依賴張量和自動微分。稍后,我們將介紹一個更簡潔的實現(xiàn),利用深度學(xué)習(xí)框架的花哨功能,同時保留以下結(jié)構(gòu)。
%matplotlib inline import torch from d2l import torch as d2l
%matplotlib inline from mxnet import autograd, np, npx from d2l import mxnet as d2l npx.set_np()
%matplotlib inline import jax import optax from flax import linen as nn from jax import numpy as jnp from d2l import jax as d2l
No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
%matplotlib inline import tensorflow as tf from d2l import tensorflow as d2l
3.4.1. 定義模型
在我們開始通過小批量 SGD 優(yōu)化模型參數(shù)之前,我們首先需要有一些參數(shù)。在下文中,我們通過從均值為 0 且標(biāo)準(zhǔn)差為 0.01 的正態(tài)分布中抽取隨機(jī)數(shù)來初始化權(quán)重。幻數(shù) 0.01 在實踐中通常效果很好,但您可以通過參數(shù)指定不同的值sigma。此外,我們將偏差設(shè)置為 0。注意,對于面向?qū)ο蟮脑O(shè)計,我們將代碼添加到__init__子類的方法中(在3.2.2 節(jié)d2l.Module中介紹 )。
class LinearRegressionScratch(d2l.Module): #@save """The linear regression model implemented from scratch.""" def __init__(self, num_inputs, lr, sigma=0.01): super().__init__() self.save_hyperparameters() self.w = torch.normal(0, sigma, (num_inputs, 1), requires_grad=True) self.b = torch.zeros(1, requires_grad=True)
class LinearRegressionScratch(d2l.Module): #@save
"""The linear regression model implemented from scratch."""
def __init__(self, num_inputs, lr, sigma=0.01):
super().__init__()
self.save_hyperparameters()
self.w = np.random.normal(0, sigma, (num_inputs, 1))
self.b = np.zeros(1)
self.w.attach_grad()
self.b.attach_grad()
class LinearRegressionScratch(d2l.Module): #@save
"""The linear regression model implemented from scratch."""
num_inputs: int
lr: float
sigma: float = 0.01
def setup(self):
self.w = self.param('w', nn.initializers.normal(self.sigma),
(self.num_inputs, 1))
self.b = self.param('b', nn.initializers.zeros, (1))
class LinearRegressionScratch(d2l.Module): #@save
"""The linear regression model implemented from scratch."""
def __init__(self, num_inputs, lr, sigma=0.01):
super().__init__()
self.save_hyperparameters()
w = tf.random.normal((num_inputs, 1), mean=0, stddev=0.01)
b = tf.zeros(1)
self.w = tf.Variable(w, trainable=True)
self.b = tf.Variable(b, trainable=True)
接下來,我們必須定義我們的模型,將其輸入和參數(shù)與其輸出相關(guān)聯(lián)。在(3.1.4)中使用相同的符號,對于我們的線性模型,我們簡單地采用輸入特征的矩陣向量乘積X和模型權(quán)重w,并加上偏移量b每個例子。Xw是一個向量并且b是一個標(biāo)量。由于廣播機(jī)制(參見 第 2.1.4 節(jié)),當(dāng)我們添加一個向量和一個標(biāo)量時,標(biāo)量將添加到向量的每個分量。生成的 方法 通過(在第 3.2.1 節(jié)中介紹 )forward在類中注冊。LinearRegressionScratchadd_to_class
@d2l.add_to_class(LinearRegressionScratch) #@save def forward(self, X): return torch.matmul(X, self.w) + self.b
@d2l.add_to_class(LinearRegressionScratch) #@save def forward(self, X): return np.dot(X, self.w) + self.b
@d2l.add_to_class(LinearRegressionScratch) #@save def forward(self, X): return jnp.matmul(X, self.w) + self.b
@d2l.add_to_class(LinearRegressionScratch) #@save def forward(self, X): return tf.matmul(X, self.w) + self.b
3.4.2. 定義損失函數(shù)
由于更新我們的模型需要采用損失函數(shù)的梯度,因此我們應(yīng)該首先定義損失函數(shù)。這里我們使用(3.1.5)中的平方損失函數(shù)。在實現(xiàn)中,我們需要將真實值轉(zhuǎn)換y為預(yù)測值的形狀 y_hat。以下方法返回的結(jié)果也將具有與y_hat. 我們還返回小批量中所有示例的平均損失值。
@d2l.add_to_class(LinearRegressionScratch) #@save def loss(self, y_hat, y): l = (y_hat - y) ** 2 / 2 return l.mean()
@d2l.add_to_class(LinearRegressionScratch) #@save def loss(self, y_hat, y): l = (y_hat - y) ** 2 / 2 return l.mean()
@d2l.add_to_class(LinearRegressionScratch) #@save
def loss(self, params, X, y, state):
y_hat = state.apply_fn({'params': params}, *X) # X unpacked from a tuple
l = (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
return l.mean()
@d2l.add_to_class(LinearRegressionScratch) #@save def loss(self, y_hat, y): l = (y_hat - y) ** 2 / 2 return tf.reduce_mean(l)
3.4.3. 定義優(yōu)化算法
正如第 3.1 節(jié)中所討論的,線性回歸有一個封閉形式的解決方案。然而,我們這里的目標(biāo)是說明如何訓(xùn)練更通用的神經(jīng)網(wǎng)絡(luò),這需要我們教您如何使用小批量 SGD。因此,我們將借此機(jī)會介紹您的第一個 SGD 工作示例。在每一步,使用從我們的數(shù)據(jù)集中隨機(jī)抽取的小批量,我們估計損失相對于參數(shù)的梯度。接下來,我們朝著可能減少損失的方向更新參數(shù)。
以下代碼應(yīng)用更新,給定一組參數(shù),一個學(xué)習(xí)率lr。由于我們的損失是按小批量的平均值計算的,因此我們不需要根據(jù)批量大小調(diào)整學(xué)習(xí)率。在后面的章節(jié)中,我們將研究如何為分布式大規(guī)模學(xué)習(xí)中出現(xiàn)的非常大的小批量調(diào)整學(xué)習(xí)率。現(xiàn)在,我們可以忽略這種依賴性。
我們定義我們的SGD類,它是d2l.HyperParameters (在第 3.2.1 節(jié)中介紹的)的一個子類,以具有與內(nèi)置 SGD 優(yōu)化器類似的 API。我們更新方法中的參數(shù)step 。該zero_grad方法將所有梯度設(shè)置為 0,這必須在反向傳播步驟之前運行。
class SGD(d2l.HyperParameters): #@save """Minibatch stochastic gradient descent.""" def __init__(self, params, lr): self.save_hyperparameters() def step(self): for param in self.params: param -= self.lr * param.grad def zero_grad(self): for param in self.params: if param.grad is not None: param.grad.zero_()
We define our SGD class, a subclass of d2l.HyperParameters (introduced in Section 3.2.1), to have a similar API as the built-in SGD optimizer. We update the parameters in the step method. It accepts a batch_size argument that can be ignored.
class SGD(d2l.HyperParameters): #@save
"""Minibatch stochastic gradient descent."""
def __init__(self, params, lr):
self.save_hyperparameters()
def step(self, _):
for param in self.params:
param -= self.lr * param.grad
class SGD(d2l.HyperParameters): #@save
"""Minibatch stochastic gradient descent."""
# The key transformation of Optax is the GradientTransformation
# defined by two methods, the init and the update.
# The init initializes the state and the update transforms the gradients.
# https://github.com/deepmind/optax/blob/master/optax/_src/transform.py
def __init__(self, lr):
self.save_hyperparameters()
def init(self, params):
# Delete unused params
del params
return optax.EmptyState
def update(self, updates, state, params=None):
del params
# When state.apply_gradients method is called to update flax's
# train_state object, it internally calls optax.apply_updates method
# adding the params to the update equation defined below.
updates = jax.tree_util.tree_map(lambda g: -self.lr * g, updates)
return updates, state
def __call__():
return optax.GradientTransformation(self.init, self.update)
We define our SGD class, a subclass of d2l.HyperParameters (introduced in Section 3.2.1), to have a similar API as the built-in SGD optimizer. We update the parameters in the apply_gradients method. It accepts a list of parameter and gradient pairs.
class SGD(d2l.HyperParameters): #@save
"""Minibatch stochastic gradient descent."""
def __init__(self, lr):
self.save_hyperparameters()
def apply_gradients(self, grads_and_vars):
for grad, param in grads_and_vars:
param.assign_sub(self.lr * grad)
接下來我們定義configure_optimizers方法,它返回類的一個實例SGD。
@d2l.add_to_class(LinearRegressionScratch) #@save def configure_optimizers(self): return SGD([self.w, self.b], self.lr)
@d2l.add_to_class(LinearRegressionScratch) #@save def configure_optimizers(self): return SGD([self.w, self.b], self.lr)
@d2l.add_to_class(LinearRegressionScratch) #@save def configure_optimizers(self): return SGD(self.lr)
@d2l.add_to_class(LinearRegressionScratch) #@save def configure_optimizers(self): return SGD(self.lr)
3.4.4. 訓(xùn)練
現(xiàn)在我們已經(jīng)準(zhǔn)備好所有的部分(參數(shù)、損失函數(shù)、模型和優(yōu)化器),我們準(zhǔn)備好實施主要的訓(xùn)練循環(huán)。理解這段代碼至關(guān)重要,因為您將對本書涵蓋的所有其他深度學(xué)習(xí)模型使用類似的訓(xùn)練循環(huán)。在每個epoch中,我們遍歷整個訓(xùn)練數(shù)據(jù)集,通過每個示例一次(假設(shè)示例的數(shù)量可以被批量大小整除)。在每次迭代中,我們獲取一小批訓(xùn)練示例,并通過模型的 training_step方法計算其損失。接下來,我們計算每個參數(shù)的梯度。最后,我們將調(diào)用優(yōu)化算法來更新模型參數(shù)。總之,我們將執(zhí)行以下循環(huán):
初始化參數(shù)(w,b)
重復(fù)直到完成
計算梯度 g←?(w,b)1|B|∑i∈Bl(x(i),y(i),w,b)
更新參數(shù) (w,b)←(w,b)?ηg
回想一下,我們在3.3 節(jié)中生成的綜合回歸數(shù)據(jù)集 不提供驗證數(shù)據(jù)集。然而,在大多數(shù)情況下,我們將使用驗證數(shù)據(jù)集來衡量我們的模型質(zhì)量。在這里,我們在每個時期通過一次驗證數(shù)據(jù)加載器來衡量模型性能。按照我們的面向?qū)ο笤O(shè)計,prepare_batch和fit_epoch方法注冊在d2l.Trainer類中(在 3.2.4 節(jié)中介紹)。
@d2l.add_to_class(d2l.Trainer) #@save
def prepare_batch(self, batch):
return batch
@d2l.add_to_class(d2l.Trainer) #@save
def fit_epoch(self):
self.model.train()
for batch in self.train_dataloader:
loss = self.model.training_step(self.prepare_batch(batch))
self.optim.zero_grad()
with torch.no_grad():
loss.backward()
if self.gradient_clip_val > 0: # To be discussed later
self.clip_gradients(self.gradient_clip_val, self.model)
self.optim.step()
self.train_batch_idx += 1
if self.val_dataloader is None:
return
self.model.eval()
for batch in self.val_dataloader:
with torch.no_grad():
self.model.validation_step(self.prepare_batch(batch))
self.val_batch_idx += 1
@d2l.add_to_class(d2l.Trainer) #@save
def prepare_batch(self, batch):
return batch
@d2l.add_to_class(d2l.Trainer) #@save
def fit_epoch(self):
for batch in self.train_dataloader:
with autograd.record():
loss = self.model.training_step(self.prepare_batch(batch))
loss.backward()
if self.gradient_clip_val > 0:
self.clip_gradients(self.gradient_clip_val, self.model)
self.optim.step(1)
self.train_batch_idx += 1
if self.val_dataloader is None:
return
for batch in self.val_dataloader:
self.model.validation_step(self.prepare_batch(batch))
self.val_batch_idx += 1
@d2l.add_to_class(d2l.Trainer) #@save
def prepare_batch(self, batch):
return batch
@d2l.add_to_class(d2l.Trainer) #@save
def fit_epoch(self):
self.model.training = True
if self.state.batch_stats:
# Mutable states will be used later (e.g., for batch norm)
for batch in self.train_dataloader:
(_, mutated_vars), grads = self.model.training_step(self.state.params,
self.prepare_batch(batch),
self.state)
self.state = self.state.apply_gradients(grads=grads)
# Can be ignored for models without Dropout Layers
self.state = self.state.replace(
dropout_rng=jax.random.split(self.state.dropout_rng)[0])
self.state = self.state.replace(batch_stats=mutated_vars['batch_stats'])
self.train_batch_idx += 1
else:
for batch in self.train_dataloader:
_, grads = self.model.training_step(self.state.params,
self.prepare_batch(batch),
self.state)
self.state = self.state.apply_gradients(grads=grads)
# Can be ignored for models without Dropout Layers
self.state = self.state.replace(
dropout_rng=jax.random.split(self.state.dropout_rng)[0])
self.train_batch_idx += 1
if self.val_dataloader is None:
return
self.model.training = False
for batch in self.val_dataloader:
self.model.validation_step(self.state.params,
self.prepare_batch(batch),
self.state)
self.val_batch_idx += 1
@d2l.add_to_class(d2l.Trainer) #@save
def prepare_batch(self, batch):
return batch
@d2l.add_to_class(d2l.Trainer) #@save
def fit_epoch(self):
self.model.training = True
for batch in self.train_dataloader:
with tf.GradientTape() as tape:
loss = self.model.training_step(self.prepare_batch(batch))
grads = tape.gradient(loss, self.model.trainable_variables)
if self.gradient_clip_val > 0:
grads = self.clip_gradients(self.gradient_clip_val, grads)
self.optim.apply_gradients(zip(grads, self.model.trainable_variables))
self.train_batch_idx += 1
if self.val_dataloader is None:
return
self.model.training = False
for batch in self.val_dataloader:
self.model.validation_step(self.prepare_batch(batch))
self.val_batch_idx += 1
我們幾乎準(zhǔn)備好訓(xùn)練模型,但首先我們需要一些數(shù)據(jù)來訓(xùn)練。這里我們使用SyntheticRegressionData類并傳入一些基本參數(shù)。然后,我們用學(xué)習(xí)率訓(xùn)練我們的模型lr=0.03并設(shè)置max_epochs=3。請注意,一般來說,epoch 的數(shù)量和學(xué)習(xí)率都是超參數(shù)。一般來說,設(shè)置超參數(shù)很棘手,我們通常希望使用 3 路分割,一組用于訓(xùn)練,第二組用于超參數(shù)選擇,第三組保留用于最終評估。我們暫時省略這些細(xì)節(jié),但稍后會對其進(jìn)行修改。
model = LinearRegressionScratch(2, lr=0.03) data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2) trainer = d2l.Trainer(max_epochs=3) trainer.fit(model, data)
model = LinearRegressionScratch(2, lr=0.03) data = d2l.SyntheticRegressionData(w=np.array([2, -3.4]), b=4.2) trainer = d2l.Trainer(max_epochs=3) trainer.fit(model, data)
model = LinearRegressionScratch(2, lr=0.03) data = d2l.SyntheticRegressionData(w=jnp.array([2, -3.4]), b=4.2) trainer = d2l.Trainer(max_epochs=3) trainer.fit(model, data)
model = LinearRegressionScratch(2, lr=0.03) data = d2l.SyntheticRegressionData(w=tf.constant([2, -3.4]), b=4.2) trainer = d2l.Trainer(max_epochs=3) trainer.fit(model, data)
因為我們自己合成了數(shù)據(jù)集,所以我們確切地知道真正的參數(shù)是什么。因此,我們可以通過將真實參數(shù)與我們通過訓(xùn)練循環(huán)學(xué)到的參數(shù)進(jìn)行比較來評估我們在訓(xùn)練中的成功。事實上,他們彼此非常接近。
print(f'error in estimating w: {data.w - model.w.reshape(data.w.shape)}')
print(f'error in estimating b: {data.b - model.b}')
error in estimating w: tensor([ 0.1006, -0.1535], grad_fn=) error in estimating b: tensor([0.2132], grad_fn= )
print(f'error in estimating w: {data.w - model.w.reshape(data.w.shape)}')
print(f'error in estimating b: {data.b - model.b}')
error in estimating w: [ 0.10755348 -0.13104177] error in estimating b: [0.18908024]
params = trainer.state.params
print(f"error in estimating w: {data.w - params['w'].reshape(data.w.shape)}")
print(f"error in estimating b: {data.b - params['b']}")
error in estimating w: [ 0.06764424 -0.183249 ] error in estimating b: [0.23523378]
print(f'error in estimating w: {data.w - tf.reshape(model.w, data.w.shape)}')
print(f'error in estimating b: {data.b - model.b}')
error in estimating w: [ 0.08918679 -0.11773038] error in estimating b: [0.211231]
我們不應(yīng)該把準(zhǔn)確恢復(fù)地面實況參數(shù)的能力視為理所當(dāng)然。一般來說,對于深度模型,參數(shù)的唯一解是不存在的,即使對于線性模型,只有當(dāng)沒有特征與其他特征線性相關(guān)時,才有可能準(zhǔn)確地恢復(fù)參數(shù)。然而,在機(jī)器學(xué)習(xí)中,我們通常不太關(guān)心恢復(fù)真正的底層參數(shù),而更關(guān)心導(dǎo)致高度準(zhǔn)確預(yù)測的參數(shù) ( Vapnik, 1992 )。幸運的是,即使在困難的優(yōu)化問題上,隨機(jī)梯度下降通常也能找到非常好的解決方案,部分原因在于,對于深度網(wǎng)絡(luò),存在許多導(dǎo)致高精度預(yù)測的參數(shù)配置。
3.4.5. 概括
在本節(jié)中,我們通過實施功能齊全的神經(jīng)網(wǎng)絡(luò)模型和訓(xùn)練循環(huán),朝著設(shè)計深度學(xué)習(xí)系統(tǒng)邁出了重要一步。在這個過程中,我們構(gòu)建了數(shù)據(jù)加載器、模型、損失函數(shù)、優(yōu)化程序以及可視化和監(jiān)控工具。為此,我們編寫了一個 Python 對象,其中包含用于訓(xùn)練模型的所有相關(guān)組件。雖然這還不是專業(yè)級的實現(xiàn),但它具有完美的功能,并且像這樣的代碼已經(jīng)可以幫助您快速解決小問題。在接下來的部分中,我們將看到如何更簡潔 (避免樣板代碼)和更高效(充分利用我們的 GPU)。
3.4.6. 練習(xí)
如果我們將權(quán)重初始化為零會發(fā)生什么。該算法仍然有效嗎?如果我們用方差初始化參數(shù)會怎樣1,000而不是0.01?
假設(shè)您是Georg Simon Ohm,正在嘗試建立一個與電壓和電流相關(guān)的電阻器模型。您可以使用自動微分來學(xué)習(xí)模型的參數(shù)嗎?
你能用普朗克定律通過光譜能量密度來確定物體的溫度嗎?作為參考,光譜密度B從黑體發(fā)出的輻射是 B(λ,T)=2hc2λ5?(exp?hcλkT?1)?1. 這里λ是波長,T是溫度, c是光速,h是普朗克量子,并且 k是玻爾茲曼常數(shù)。您測量不同波長的能量λ現(xiàn)在您需要使譜密度曲線符合普朗克定律。
如果你想計算損失的二階導(dǎo)數(shù),你可能會遇到什么問題?你會如何修復(fù)它們?
為什么函數(shù)reshape中需要方法loss?
嘗試使用不同的學(xué)習(xí)率來找出損失函數(shù)值下降的速度。你能通過增加訓(xùn)練的次數(shù)來減少錯誤嗎?
如果樣本數(shù)不能除以批量大小,那么在data_iter一個紀(jì)元結(jié)束時會發(fā)生什么?
嘗試實現(xiàn)不同的損失函數(shù),例如絕對值損失。(y_hat - d2l.reshape(y, y_hat.shape)).abs().sum()
檢查常規(guī)數(shù)據(jù)會發(fā)生什么。
如果您主動擾亂某些條目,請檢查行為是否存在差異y, 例如 y5=10,000.
你能想出一個便宜的解決方案來結(jié)合平方損失和絕對值損失的最佳方面嗎?提示:如何避免非常大的梯度值?
為什么我們需要重新洗牌數(shù)據(jù)集?你能設(shè)計一個惡意數(shù)據(jù)集否則會破壞優(yōu)化算法的情況嗎?
-
pytorch
+關(guān)注
關(guān)注
2文章
808瀏覽量
13252
發(fā)布評論請先 登錄
相關(guān)推薦
利用Arm Kleidi技術(shù)實現(xiàn)PyTorch優(yōu)化
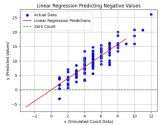
基于RK3568國產(chǎn)處理器教學(xué)實驗箱操作案例分享:一元線性回歸實驗
什么是回歸測試_回歸測試的測試策略
如何使用 PyTorch 進(jìn)行強(qiáng)化學(xué)習(xí)
pytorch怎么在pycharm中運行
pycharm如何調(diào)用pytorch
如何構(gòu)建多層神經(jīng)網(wǎng)絡(luò)
如何在PyTorch中實現(xiàn)LeNet-5網(wǎng)絡(luò)
PyTorch的介紹與使用案例
tensorflow和pytorch哪個更簡單?
如何使用PyTorch建立網(wǎng)絡(luò)模型
從頭開始構(gòu)建 RISC-V CPU使用分立邏輯芯片,通過最熱門的新架構(gòu)構(gòu)建功能驚人的 CPU
為什么STM32F103C8T6程序執(zhí)行到0.425秒就從頭開始?
深入探討線性回歸與柏松回歸
基于嵌入式OS的LwIP協(xié)議棧




 PyTorch教程-3.4. 從頭開始執(zhí)行線性回歸
PyTorch教程-3.4. 從頭開始執(zhí)行線性回歸










評論