昨天關于跨導Gm的結論還是有點粗糙,應該說跨導很復雜,和溝道的特性有關系;需要分開討論,我們先試著了解導電溝道電流是怎么算的:

如圖,電流分擴散電流和漂移電流,工作時的mosfet電流很大,主要是漂移電流,因此忽略掉擴散電流的成分。
同時我們討論平面MOS,導電溝道主要是柵極下面薄薄的一層(y方向上),x方向上的電場我們也忽略掉。
最后我們得到,溝道中某截面的電流密度Jn和溝道遷移率μ,溝道中載流子濃度n,以及截面上此點的電勢Φ有關。

上上圖是求得電流密度 J,此圖我們求電流,就是對電流密度做關于體積的積分,溝道y方向上的長度為L,溝道寬度為Z,最后得到電流ID(既是溝道電流也可以看成漏極電流)

這個Z有的文獻里面也會寫成W,這個公式表明,溝道電流Id大小與溝道寬長比W/L成正比,也和溝道內的電荷密度QN成正比,同時也是電勢Φ從0到Vds(從源級到漏極)的積分。
現在要求這個積分,主要是求電荷密度QN,場效應管的QN不知道,我們可以通過MOS電容的電荷分布來近似。
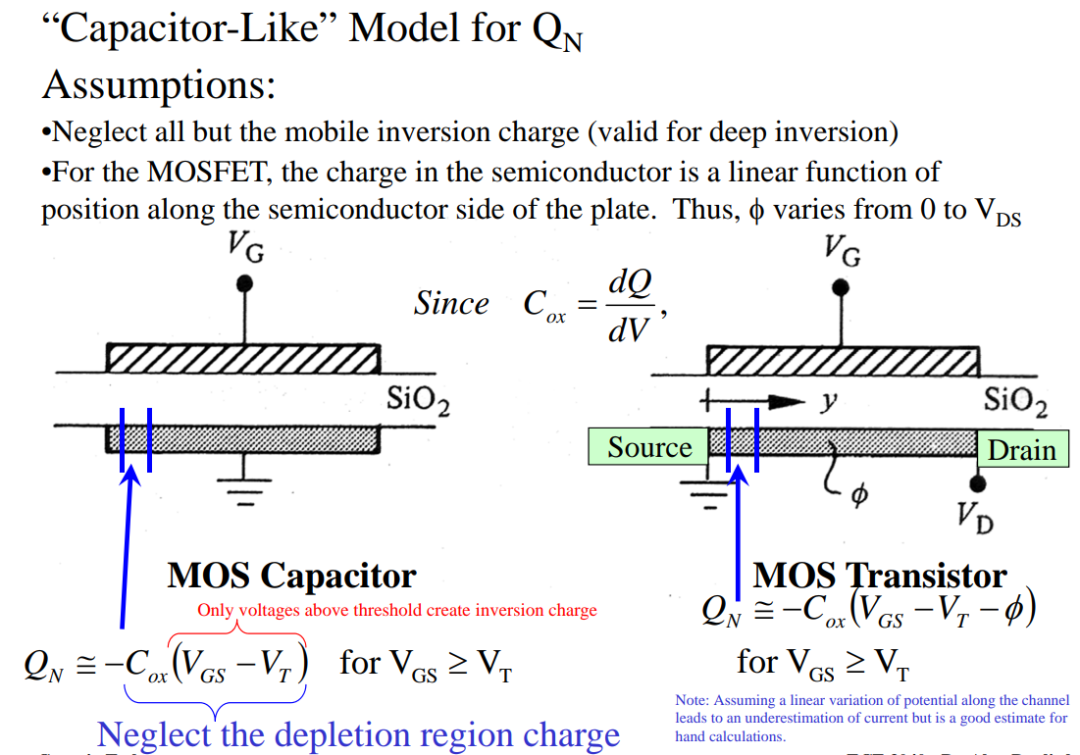
左邊就是一個最簡化的MOS電容模型,上極板接電壓VG,中間的介電材料是SiO2,標準的平行板電容器。當VG值>閾值電壓Vt,反型層建立,溝道的總電荷密度QN就是柵電容乘以電容兩端的電勢差。
那么對比一下,從MOS電容到MOS晶體管,無非就是加了源級D和漏極S,其中漏極S還是接地的,電壓為0,所以,只加入了源級電壓VD,那么,溝道從漏極到源級(D到S),無非是每個點的電勢不一樣,最小是0,最大是VD,僅此而已。
所以接下來就好辦了,直接設溝道上某處的電勢為Φ,那么此處的電荷密度QN和MOS電容計算方法一樣,也是柵電容Cox乘以電勢差(VG-Vt-Φ)
代入到上面電流ID的公式,
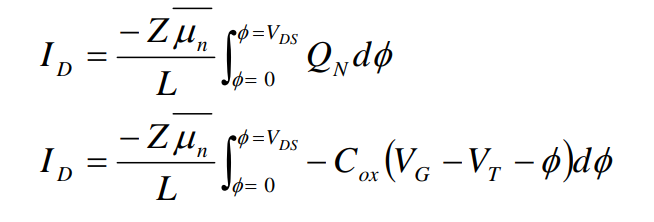
然后對溝道上的每個點的電勢進行積分(積分下限是源極的0V,積分上限是漏極的VD),把電勢看成變量,其余為常量,被積函數是最簡單的一次方程,那么原函數就是二次方程;

這個方程就是上篇文章的薩支唐方程,描述了MOSFET的輸出電流與柵極電壓,漏極電壓的關系。
需要注意的是,這個方程使用條件有兩個,首先是要MOS溝道完全開啟,也就是VGS要大于閾值電壓Vt,其次溝道不能夾斷,也就是VDS要小于VDsat(預夾斷電壓/飽和電壓)。
這個夾斷點的電壓怎么計算?看圖
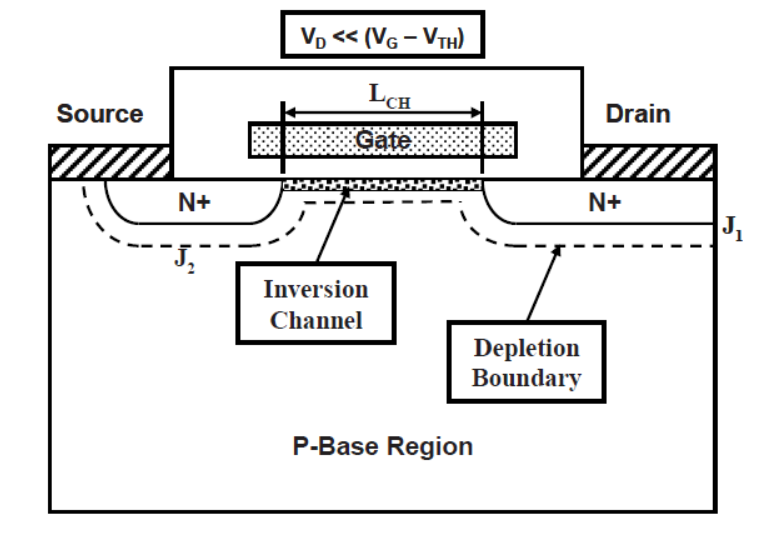
分4種類型討論;
1: 溝道開啟,漏極電壓VDS遠小于柵極電壓和閾值電壓的差值VG-Vth,此時二階量直接忽略:
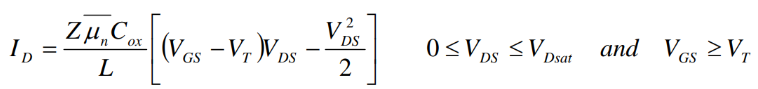
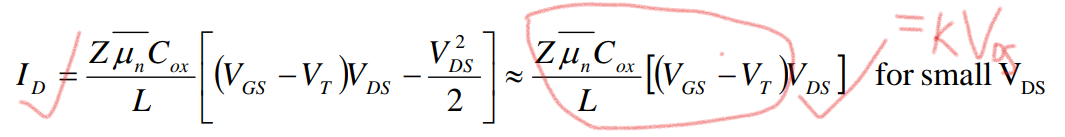
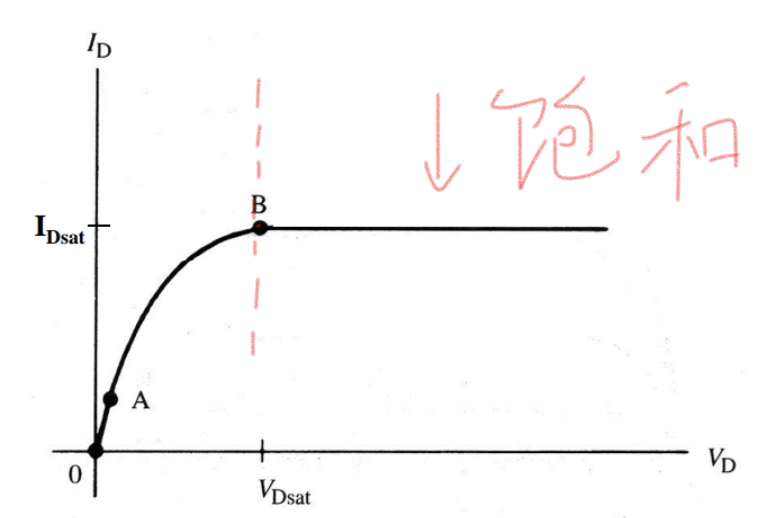
得到ID和VDS線性相關,對應的就是MOSFET輸出特性曲線的線性區:
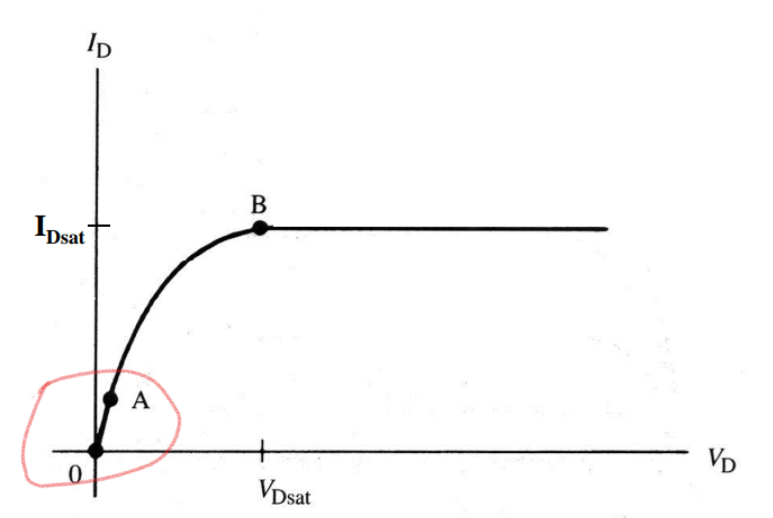
對應的是輸出特性曲線上0-A這一段直線。
2: 溝道開啟,漏極電壓VDS增大,依然不大于柵壓和閾值電壓之差VGS-Vth。那么此時溝道內由于右邊電勢為VDS,左邊VS=0,必然會出現溝道右邊電勢高,左邊電勢低的情況,那么,溝道右邊的反型層處電勢=VGS-Vth-VDS,會變小,最右邊柵極的影響力被漏極抵消一部分,一部分本來可以柵吸引形成溝道的電子,就被漏極正電壓拉過去了,右邊的反型層便逐漸減弱,溝道在靠近右邊漏極區域慢慢變窄,于是電流能力變得沒那么強。
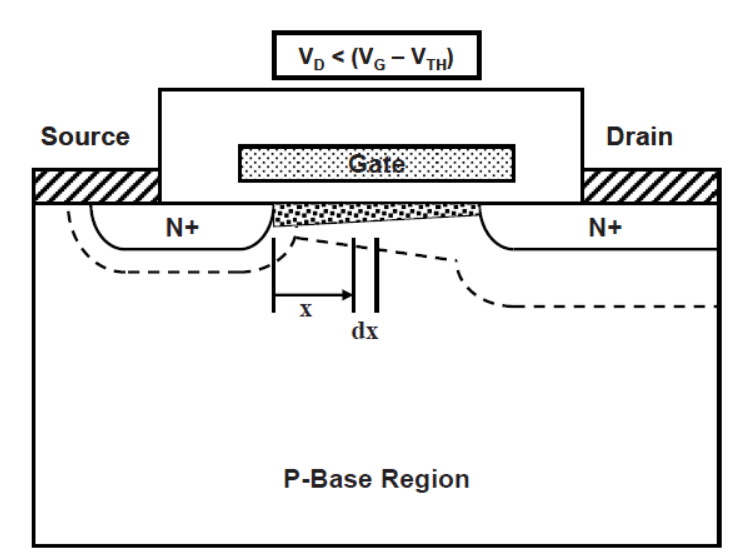
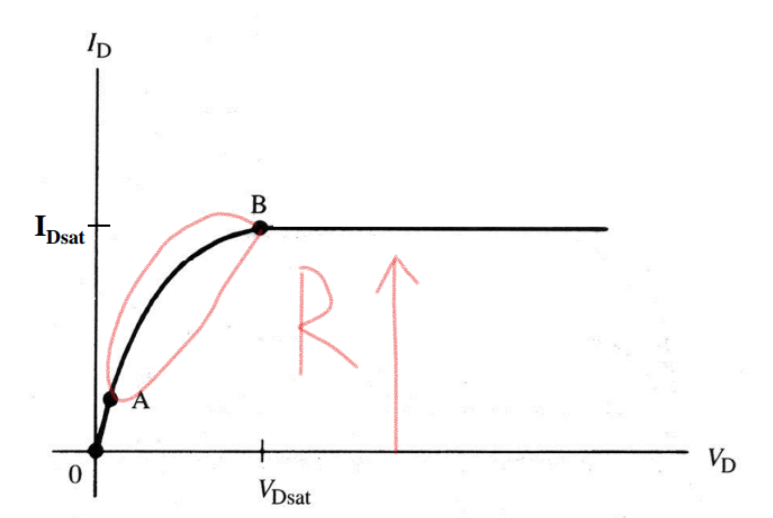
反應在輸出特性曲線上就是電流上升速度變慢,導通阻抗變大:A到B這一段
3: 預夾斷點(pinch-off),當電流繼續上升,漏極電壓VDS持續增大,達到VDS=VGS-Vth這個點時,此時溝道的最右邊終于頂不住了,由于VGS-Vth電勢沒有VDS高,這里已經沒有反型層了,也就是導電溝道在這里開始消失了。
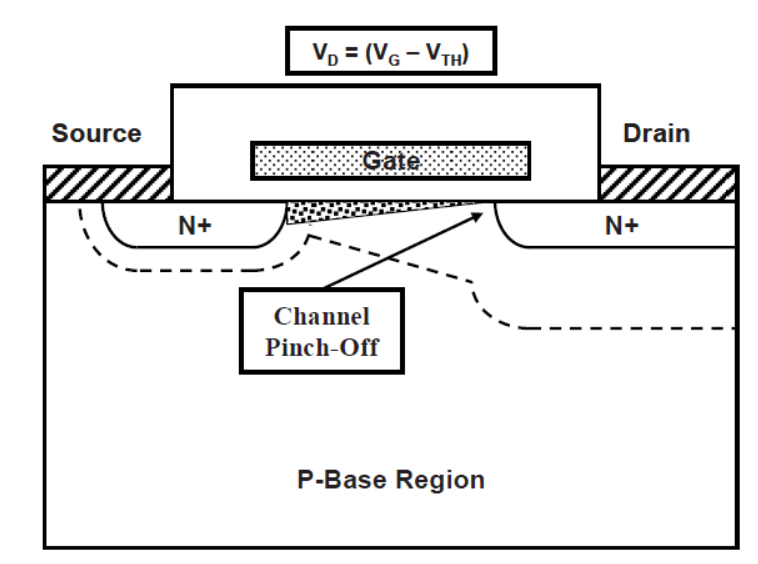
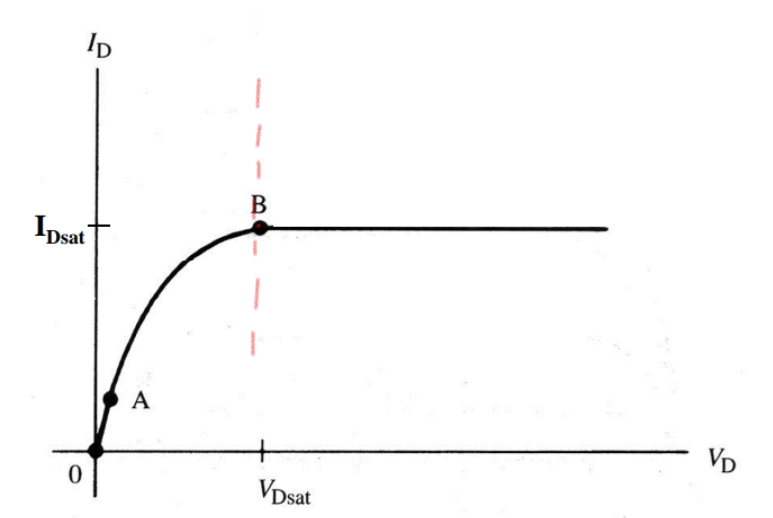
反映在輸出特性曲線上就是漏極電流飽和了,再也無法靠提升VDS來提升了,除非提升柵壓,否則電流是無法上升的。
4: 完全夾斷(飽和區)
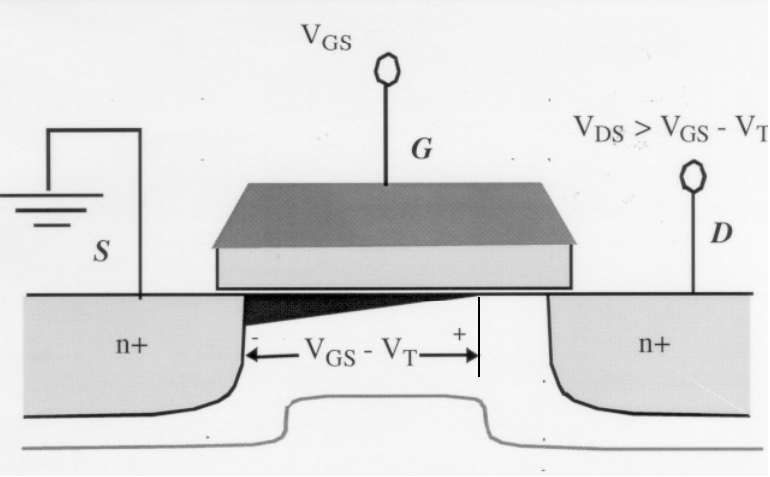
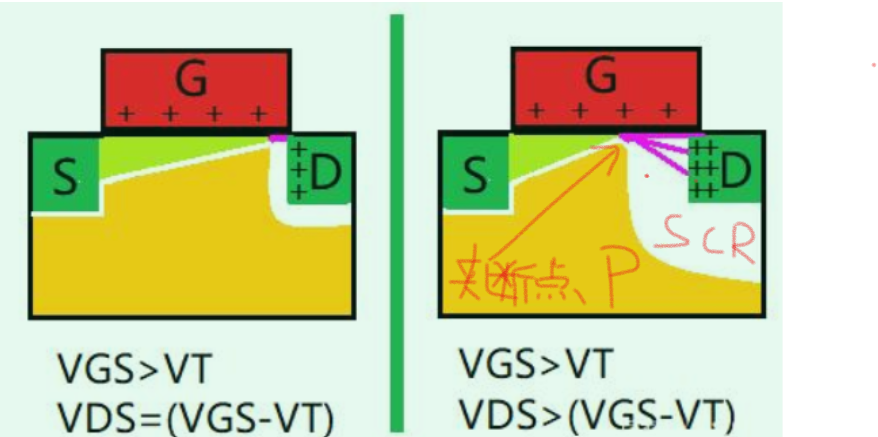
溝道完全夾斷之后,源級到漏極之間的導電溝道斷了一部分,也就是說電子只能沿著溝道跑到中間,然后溝道不見了,不過為什么還是有電流呢?
因為夾斷點后面支撐它的不是原來的黃色P型區域,而是電壓升高更吸引電子的漏極D及其空間電荷區(白色SCR) 。因此電子沖入空間電荷區,就相當于幾乎沒有阻擋的準自由電子快速被漏極收集。所以雖然溝道夾斷了,但是電流依然還在。
-
電容器
+關注
關注
64文章
6240瀏覽量
99888 -
MOSFET
+關注
關注
147文章
7203瀏覽量
213661 -
場效應管
+關注
關注
47文章
1166瀏覽量
64078 -
MOS管
+關注
關注
108文章
2426瀏覽量
67113 -
VDS
+關注
關注
0文章
45瀏覽量
10752
發布評論請先 登錄
相關推薦
解答74HC14中正向閾值電壓和負向閾值電壓是什么/電壓為多少
MOS管閾值電壓的問題
遲滯比較器閾值電壓除了由我的電阻參數設定還要其他因素嗎?
閾值電壓的計算

MOS管閾值電壓與溝長和溝寬的關系
GaN基MIS-HEMTs閾值電壓漂移的快速動力學論文免費下載
如何突破EDA封鎖 卷起來的閾值電壓
不同Vt cell工藝是怎么實現的?閾值電壓和哪些因素有關系?
影響MOSFET閾值電壓的因素
什么是MOS管亞閾值電壓?MOSFET中的閾值電壓是如何產生的?
MOSFET閾值電壓是什么?影響MOSFET閾值電壓的因素有哪些?




 溝道反型層閾值電壓Vth介紹
溝道反型層閾值電壓Vth介紹










評論