今天聊一聊矩形脈沖,談他只因為常見,工作中常用。
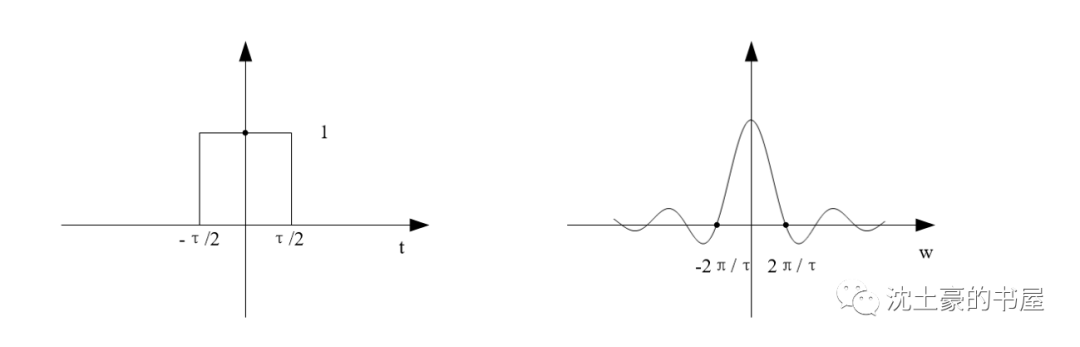
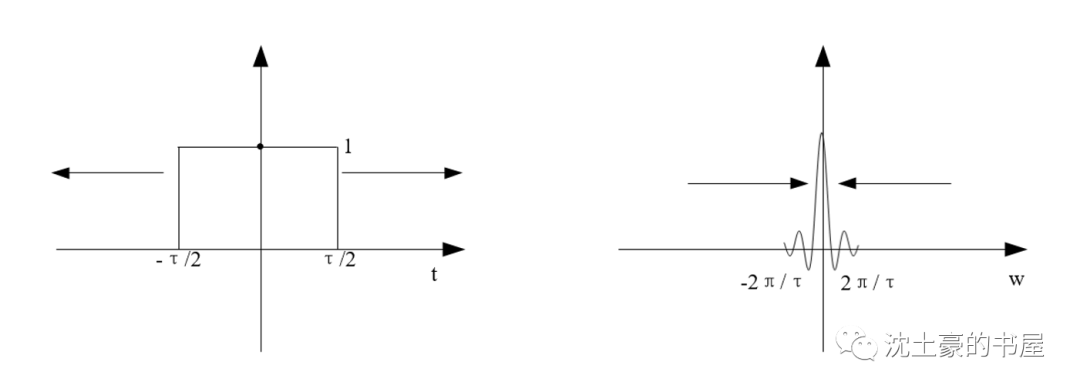
左圖是個門函數,寬度為τ,高度為1,自變量t。
右圖是門函數經過傅里葉變換的頻譜密度函數
F(jw),自變量w。
兩種變換對等,包含信號的所有信息量,僅僅是一種數學的變換域。
其傅里葉變換對如下式:
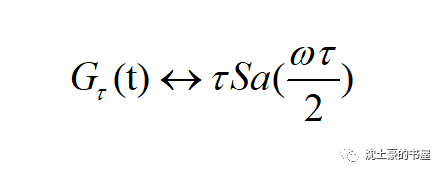
case1:
我們把門寬度縮小,即τ→0,或者很小很小,獲得一個尖脈沖。(研究它的目的是尖峰噪聲,都是小的脈沖,振蕩的,時間寬度小的,尖刺的…)
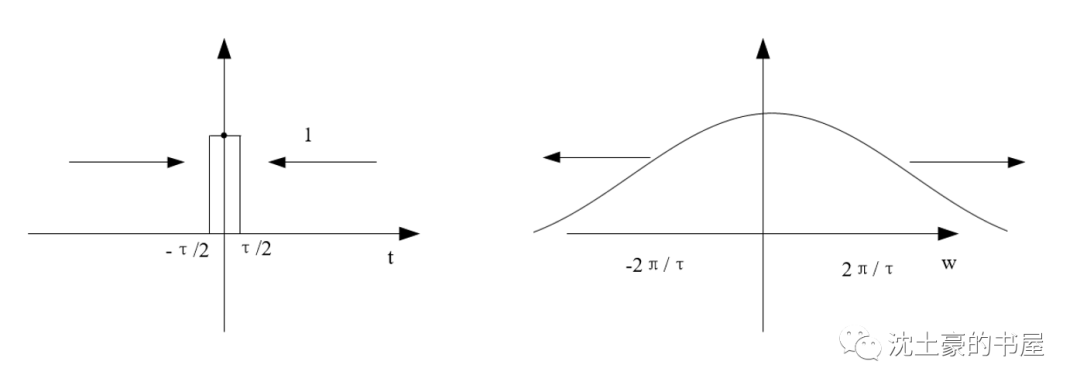
長的很像沖激函數吧~就高度不一樣嘛
再看看沖激函數的FT,正好是1。
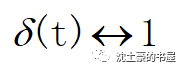
我們把門函數的FT即τSa(wτ/2),令τ趨于0,數無形時少直覺,右圖一看,第一過零點直接趨于無窮大,Sa()函數中間凸起來的區域一條直線~不就長得像1嗎?
case2:
我們把門寬度放大,即τ→很大,或者很大很大,獲得一個直流信號。
再看看直流信號的FT,是個沖激。
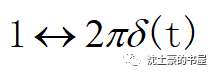
我們把門函數的FT即τSa(wτ/2),如果忽略前面的系數τ,并令τ趨于+∞。數無形時少直覺,右圖一看,第一過零點直接趨于無窮小,Sa()函數中間凸起來的區域逼近于0~不就長得像沖激函數嗎?
case3:
由尺度變換公式
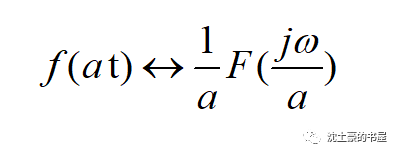
得
時域壓縮信號,將會使得頻譜密度函數頻率軸伸展,信號的頻率分量會 向高頻擴散 。
時域擴展信號,將會使得頻譜密度函數頻率軸收縮,信號的頻率分量會 向低頻聚集 。
或者說:對于一個脈沖信號,信號越窄,頻譜密度函數 收斂性變差 ,Sa()函數第一過零點帶寬往后推,幅度較高的頻率分量往后搬移。
以后應當有認知:
- 尖峰噪聲具有高頻特性,尖峰越窄,信號帶寬越高。
- 時域觀察即是尖峰噪聲振蕩周期/脈沖寬度。
- 頻域觀察即使頻譜密度函數的分布情況。
REF ADI一張圖

- 上圖DCDC噪聲,開關噪聲脈沖窄,能量小,信號帶寬高。
- 紋波噪聲,振蕩周期T大,脈寬大,能量較開關噪聲大,信號帶寬等于1/T。
-
Ref
+關注
關注
0文章
19瀏覽量
28019 -
脈沖信號
+關注
關注
6文章
401瀏覽量
37338 -
DCDC芯片
+關注
關注
0文章
34瀏覽量
11148 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42895
發布評論請先 登錄
相關推薦
從焊接角度聊一聊,設計PCB的5個建議

來聊一聊Altium中Fill,Polygon Pour,Plane的區別和用法
聊一聊stm32的低功耗調試
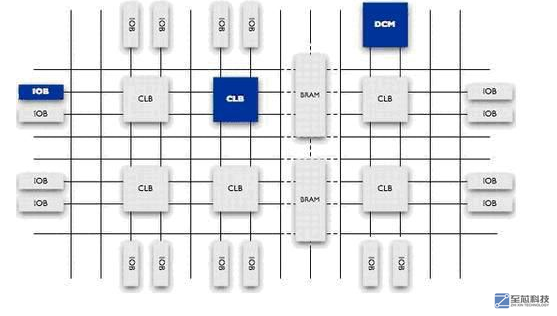
聊一聊7系列FPGA的供電部分
聊一聊FPGA的片內資源相關知識
聊一聊IIC總線設計
小米米聊2月19日停止服務 米聊宣布關閉服務器
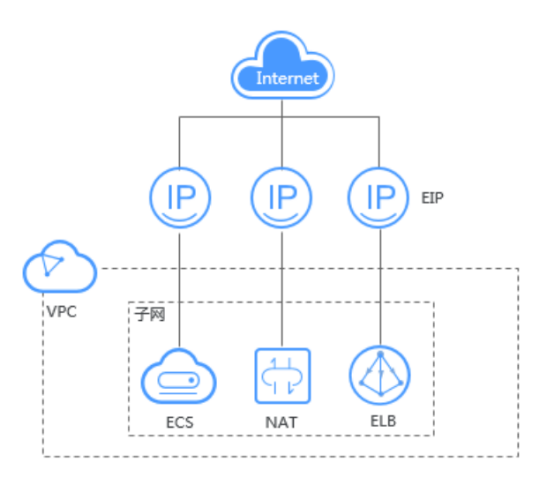
聊一聊華為云彈性公網IP的那些事兒



















評論