摘 要

當電磁波頻率增大到太赫茲頻段時，太赫茲波的波長與粗糙表面微結構可比擬。粗糙表面將對太赫茲波的傳播機理產生重要影響，散射在傳播中將發揮關鍵作用。當下針對太赫茲頻段散射特性的研究主要依靠大規模測量，較難實現。因此，使用建模的方法生成符合實際物理分布的粗糙表面，借助全波仿真的方法研究太赫茲波和表面粗糙度的作用機理是研究太赫茲波散射特性的新途徑。提出使用輪廓儀捕獲典型材料的物理分布特性，并從中提取粗糙面的關鍵統計參數。基于蒙特卡羅方法，依據統計參數重建該表面的物理分布。將測量表面和重建表面導入Feko進行全波仿真，比較并驗證該研究方案的可行性。

0 1

概 述

當下，無線通信系統面臨著2個關鍵問題：傳統頻譜資源的日益短缺和無線網絡需求的飛速增長，這迫使無線通信行業亟需開發新的頻譜資源以滿足用戶的迫切需求。在無線通信領域，有限的頻譜極其珍貴，對通信、廣播、信息網絡等領域極其重要［1］。而隨著無線通信行業的發展，較低頻段的頻譜資源已不能滿足人們對無線網絡的需求，使得無線通信行業開發更高頻段的頻譜資源以滿足市場的需求。

太赫茲（Terahertz，THz）頻段是介于毫米波和紅外波之間，頻率在0.1~10THz，它在電子學領域被稱為亞毫米波，光譜學領域被稱為遠紅外射線，是目前通信研究的熱點頻段。太赫茲波是目前電磁波譜中唯一一個沒有獲得全面研究且充分利用的波譜“空白”區［2］。在未來的通信中，太赫茲頻段的無線通信有著高數據率的潛力，有望分擔繁重的通信壓力［3］。因此，對該波段的研究是通信行業當前和未來的重點研究方向之一。對于太赫茲通信而言，由于其波長與環境中大部分表面的粗糙度可比擬，太赫茲波的傳播機理將發生重要變化，散射將成為關鍵的傳播機理。

當前針對太赫茲頻段散射特性的研究主要依賴于昂貴的太赫茲測量設備和大規模的材料測量。但是，由于太赫茲頻段恰好處于由宏觀電子學向微觀光子學過渡的頻段，目前目標材料對太赫茲波的響應機理尚且不明，目標表面可與波長比擬的細微結構對太赫茲波散射的影響規律也不清楚，同時有效的散射特性計算方法與實驗測量手段缺乏，這些問題給太赫茲頻段目標散射特性理解與太赫茲雷達技術的實際應用帶來了嚴峻挑戰。由于太赫茲的衍射和反射相比微波或者毫米波較弱，室內任何的障礙物和移動的人體都有可能破壞通信條件。太赫茲測量設備價格昂貴，實驗環境較為嚴格，對于實際實驗室測試的要求較高，實際研究成本較大，且結果易受環境影響［5］。對于太赫茲頻段電磁波的研究，傳統的實際測量研究方法不能滿足大多數情況下的研究要求，過高的測試設備要求導致研究成本昂貴。因此，電磁計算仿真成為了優選的研究方法，對于精確仿真室內環境下的太赫茲通信系統的散射十分重要。

本文利用三維輪廓儀捕獲實際粗糙面的高度分布特性，同時基于蒙特卡洛方法依照測得關鍵參數對粗糙表面進行隨機建模，借助全波仿真工具Feko進行電磁仿真，得出由實際粗糙表面和建模重新生成的粗糙表面的散射特性。比較2個表面的散射電場分布，驗證利用該方法研究粗糙面散射特性的可行性。

0 2

表征粗糙表面分布的關鍵參數

研究粗糙面表面粗糙度對散射的影響首先需要確定粗糙面的統計參數，目前已經有相關理論對粗糙面高度分布的統計量進行介紹［6］。隨機粗糙面的高度起伏均方根高度δ和表面相關長度l是描述粗糙表面高度分布特性的2個基本統計參數。

2.1 均方根高度 δ

以一維情況為例，設隨機粗糙面的高度起伏為z=f（x），它的概率密度函數p（f）反映高度起伏的分布情況［7］。粗糙面的均方根高度δ反應粗糙面粗糙程度，定義為：

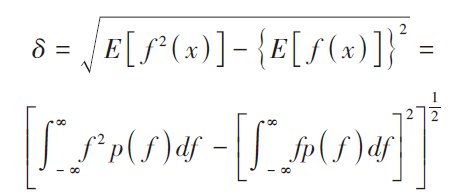
（1）

對于二維粗糙面同理，將積分域從X方向變換為XOY平面，計算得出均方根高度即可。

2.2 相關長度l

對于特定分布的粗糙表面，單一的均方根高度并不能唯一地描述粗糙面的特性，所以引入自相關函數表明隨機表面上任意2點間的關聯程度［8］，從而更準確地描述粗糙面特性，定義自相關函數為：

G(R)=E[f(x)f(x+R)]

（2）

δ2是粗糙面表面的高度方差，因此對自相關函數進行歸一化，定義相關系數為：

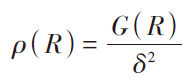
（3）

表面相關長度l是估計表面上任意2點是否相互獨立的一種基準，即若表面上2點在水平距離上相隔距離大于l，則可認為這2點的高度值在統計學上近似相互獨立。根據上述定義，將相關系數ρ(R)降為1/e時的R值稱為相關長度l，即ρ(l)=1/e。對于二維粗糙面，單一方向的相關長度不能很好的描述其任意2點間的相關性，因此引入lx，ly 2個統計參數來分別描述其不同方向的相關性。

0 3

基于蒙特卡洛法的粗糙表面建模

3.1 蒙特卡洛法

蒙特卡洛方法又稱線性濾波法[9]，其基本思想是在頻域用功率譜對其進行濾波，再對結果做逆快速傅里葉變換得到粗糙面的高度起伏。由于粗糙表面被認為由大量的諧波疊加而成［10］，諧波的振幅是獨立的高斯隨機變量，其方差正比于特定波數的功率譜密度S(k)。假設要產生的二維隨機粗糙表面在X和Y方向上的長度分別為lx和ly，等間隔離散點數分別為M和N，相鄰2點間的距離分別為Δx和Δy，則粗糙面上每一點的高度可表示為：

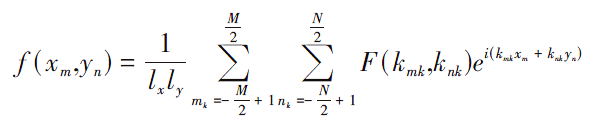
（4）

其中，

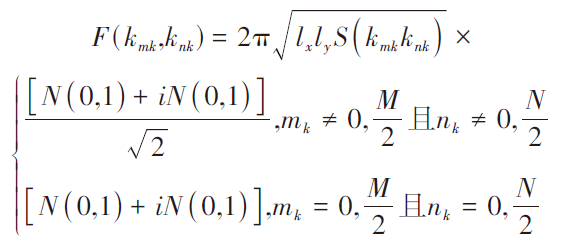
（5）

其中，離散波數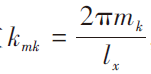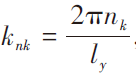，，N(0,1)表示均值為0，方差為1的正態分布隨機數。S(kmkknk)為服從高斯分布的粗糙面的功率譜函數。

3.2 實際表面的高度分布

采用某三維掃描儀［11］（掃描精度高、數據量大，能在光學掃描過程中產生極高密度數據）捕獲表面的三維物理分布，實現對材料的三維建模。對輪廓儀進行基本的校正，讓其左右相機對焦于所測材料的平面，并調整好曝光度與清晰度。將標定板置于材料平面進行標定，將所測材料貼上標定點并置于平面上，這里以瓷磚為例，待測樣本如圖1（a）所示。從不同角度掃描瓷磚，然后對所得數據進行拼接，得到瓷磚的三維模型，導出為stl文件并處理［12］，掃描拼接后的結果如圖1（b）所示。

圖1 瓷磚實物與輪廓儀掃描結果對比

提取其分布參數，借助分布擬合工具擬合粗糙表面的高度分布特性（見圖2）。從圖2可以看出，瓷磚表面的高度服從均值為0.028mm、標準差為0.135mm的高斯分布。依據式（1），擬合的標準差即為表面的均方根高度。

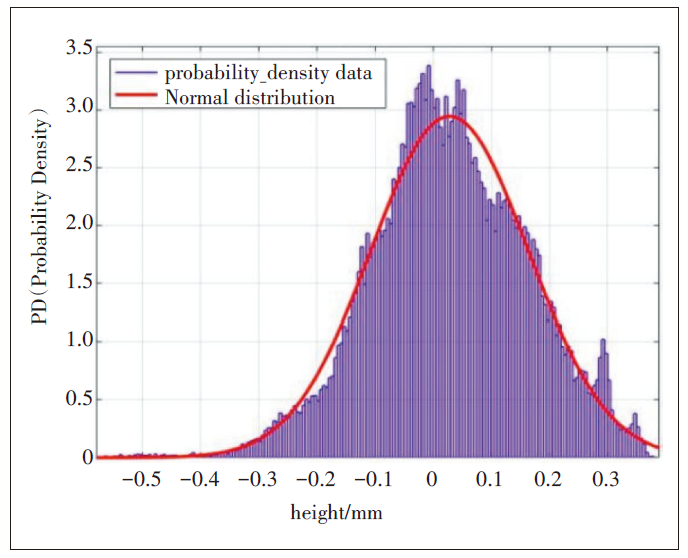
圖2 瓷磚表面高度分布擬合

基于測量數據和式（2）~（3），計算得到表面在X與Y方向的相關系數ρ(R)，如圖3所示。

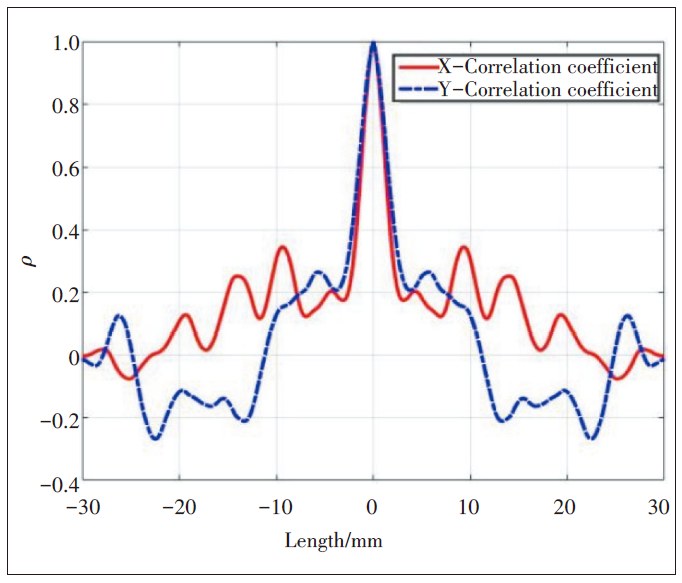
圖3 瓷磚表面相關系數

將相關系數ρ(R)降為1/e時的R值稱為相關長度l，即ρ(l)=1/e，記錄X與Y方向的相關長度。計算得出2種材料的均方根高度與相關長度，如表1所示。

表1 材料的粗糙面統計參數

3.3 基于蒙特卡洛法生成隨機粗糙面

依據式（4），通過蒙特卡洛方法[13]重建均方根高度為0.13533mm，相關長度分別為lx=1.80mm、ly=2.24mm的三維粗糙表面（見圖4）。

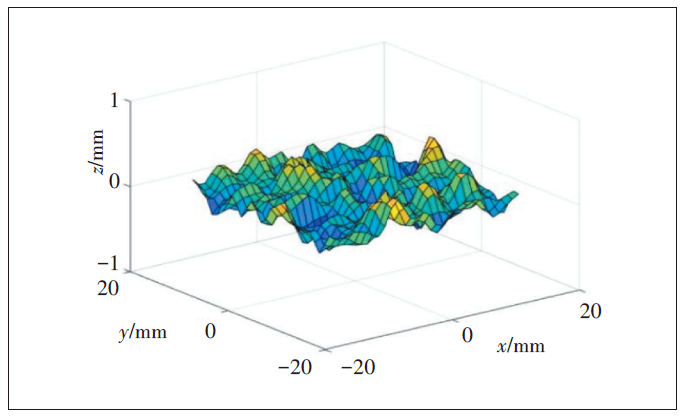
圖4 重建的隨機粗糙面

0 4

粗糙表面散射特性

Feko是一款基于積分方程方法求解麥克斯韋方程組任意結構通用的三維電磁場仿真軟件。Feko支持對外部導入的三維模型進行仿真，可以設置模型的材質、激勵源頻率和角度、求解算法等參數，還能在不同維度上對比仿真結果，能夠很好地滿足實驗需求，其電磁計算結果的準確性得到了行業的認可。

4.1 仿真設置

瑞利判據常用來判斷一個表面是否是粗糙的，瑞利判據公式如下：

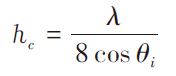
（6）

式中：

λ——波長

θi——入射角

h0——粗糙表面最大高度差，若h0大于hc，則認為表面是粗糙的，反之則可認為它是光滑的

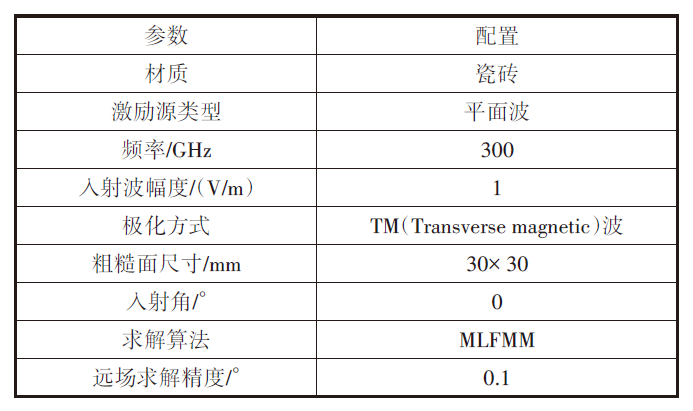
導入材料粗糙面，增加并選擇所需的參數與材質，進行網格剖分，重新劃分網格面，提升粗糙面的精度。然后采用多層快速多極子方法（Multi Level FastMultipole Method，MLFMM）［14］，基于分組思想，將規模為N的分組逐層計算單元間的相互作用，對內存的需求正比于N×log（N），極大節約了計算資源，非常適合電大尺寸結構的輻射與散射問題，依靠Feko軟件的高性能進行計算，在保證精度的前提下能夠極大降低工作量。最后設置對應頻率的激勵源與遠場參數進行求解，具體參數參考表2。

表2 仿真參數配置

4.2 結果比較

為了對比不同材質粗糙面的遠場散射特性和相同材質粗糙面的遠場散射特性，對不同獲取途徑的粗糙面進行全波仿真，得到遠場的散射電場分布如圖5所示。比較圖5（a）與圖5（b），2個粗糙表面上的散射波瓣形狀基本一致。對于粗糙表面而言，在該配置下盡管部分能量被散射到各個方向，但散射波瓣基本聚集在鏡面反射方向周圍。為更清楚地對比其散射電場分布情況，圖6是測量得到的瓷磚粗糙面和生成得到的瓷磚粗糙面的入射面散射電場在笛卡爾坐標系的結果。

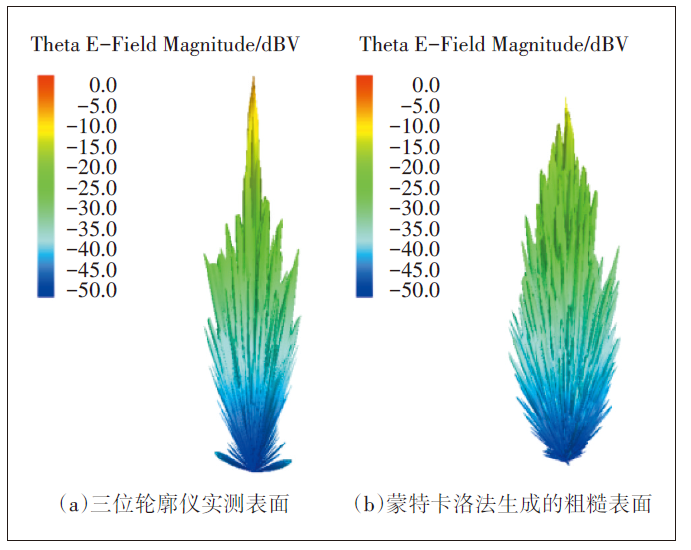
圖5 粗糙面遠場散射（3D）

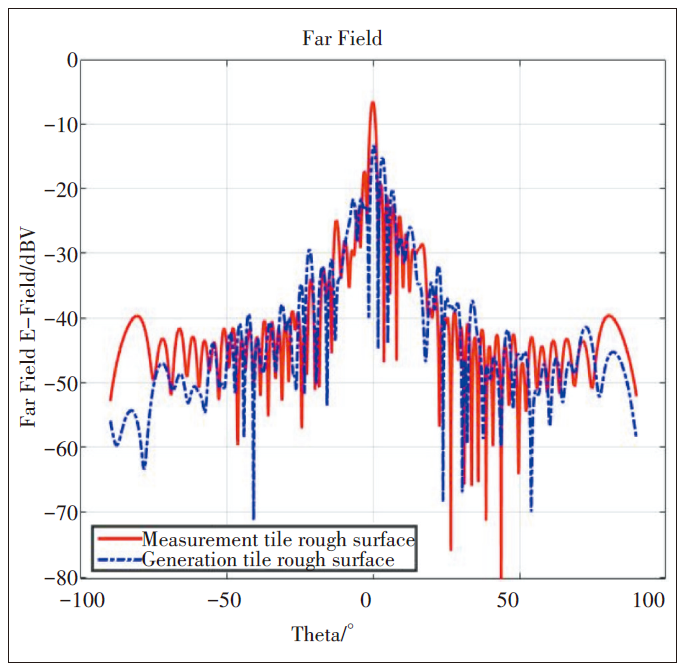
圖6 測量瓷磚與生成瓷磚粗糙面遠場

散射特性對比

首先，兩者遠場散射特性的包絡曲線整體趨勢變化大致相同，遠場電場幅值在Theta為0時達到最大，隨著Theta絕對值的增大逐漸減小；其次，兩者的波瓣均為狹窄的陡峰，形狀較為相似。這說明通過蒙特卡洛法重建的粗糙表面上散射電場的波瓣形狀和變化趨勢與實際表面基本相同，驗證了用蒙特卡洛方法建立的理想粗糙面來代替實際粗糙面進行全波仿真的可行性。

0 5

總 結

本文比較了由輪廓儀實際測量得到的粗糙表面和基于蒙特卡洛法建模生成的粗糙表面在太赫茲頻段下的散射特性，通過測量的實際粗糙面與建立理想粗糙面的仿真對比，得到了如下結論。

a）實際粗糙面的高度分布服從正態分布，證明了基于蒙特卡洛方法對粗糙面進行建模的合理性。

b）通過對比2個粗糙面在相同頻段下的散射電場分布，證明了使用蒙特卡洛方法建立的理想粗糙面以替代實際粗糙面來研究太赫茲頻段粗糙表面散射特性的可行性。

對于未來太赫茲頻段的研究，粗糙面的散射始終是一個重要的研究課題，理想粗糙面的仿真對于實際應用有很大意義［15］，在一些不便于實際測試的研究環境下，電磁計算仿真方法可以提供理想的測試環境，在一定程度上為實驗提供可靠的數據。

審核編輯 ：李倩