DPD是數字預失真的首字母縮寫,許多射頻(RF)、信號處理和嵌入式軟件開發工程師都熟悉這一術語。對于DPD,從純粹數學角度出發的建模,到微處理器實際實現面臨的限制,許多工程師都有自己獨特的見解。作為負責評估RF基站產品中DPD性能的工程師,或者是一名算法工程師,可能都會想知道數學建模技術以及在實際系統中的實現方式。如今,DPD在蜂窩通信系統中隨處可見,使功率放大器(PA)能夠有效地為天線提供最大功率。5G基站中的天線數量增加,頻譜變得更加擁擠,DPD開始成為一項關鍵技術,支持開發經濟高效且符合規格要求的蜂窩系統。
什么是DPD?為什么要使用DPD?
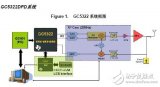
當基站射頻裝置輸出RF信號時(參見圖1),需要先將其放大,然后通過天線發射出去。放大是通過RF PA來實現的。在理想情況下,PA接收輸入信號,然后輸出與其輸入成正比的更高功率信號。PA效率應盡可能高,將放大器的大部分功耗都轉化為信號輸出功率。
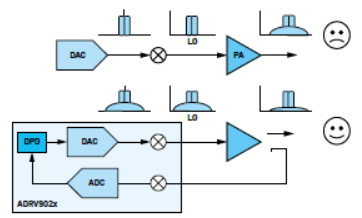
圖1:采用和未采用DPD技術的簡化射頻結構框圖。
但理想并非實際。PA由晶體管構成,晶體管是有源器件,本身具有非線性。如圖2所示,如果PA工作在“線性”(相對而言)區域,則輸出功率與輸入功率相對成比例。但缺點是PA效率很低,大部分功耗都會作為熱量流失。故希望PA工作在壓縮初始區。這意味著, PA輸出不會隨著輸入信號等比例增加,即此時輸出信號會嚴重失真。
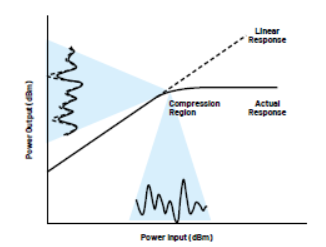
圖2:PA輸出功率與輸入功率之間的關系圖(顯示了輸出/輸入信號的投影)。
這種失真發生在頻域中的已知位置,具體取決于輸入信號。圖3顯示了這些位置,以及基頻與這些失真產物之間的關系。在RF系統中,只需要對基波信號附近的失真進行補償,這些信號是奇階交調產物。系統濾波處理帶外產物(諧波和偶階交調產物)。圖4顯示RF PA的壓縮點附近的輸出。交調產物(特別是三階)清晰可見,就像是圍繞著目標信號的“裙擺”。
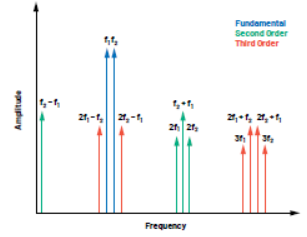
圖3:雙音輸入交調和諧波失真的位置。

圖4:2× 20 MHz信號通過SKY66391-12 RF PA,中心頻率為1850 MHz。
DPD旨在通過觀察PA輸出來表征這種失真,要了解所需輸出信號,隨之更改輸入信號,使得PA輸出接近理想值。只有在相當具體的情況下才能有效地實現這一目標。需要配置放大器和輸入信號,使放大器有一定程度的壓縮但未完全飽和。
PA失真建模背后的數學計算
在“射頻功率放大器數字預失真的廣義記憶多項式模型”一文中,開創性地介紹了針對DPD廣泛使用的廣義記憶多項式(GMP)方法。為了簡化,先嘗試拆解一下GMP方法,以更直觀地理解數學原理。
Volterra級數是DPD的重要數學基礎,它用于建立具有記憶的非線性系統模型。記憶僅僅意味著系統的當前輸出取決于當前和過去的輸入。Volterra級數很常用(所以功能強大),對于PA DPD,該級數可以精簡使用,使其在實時數字系統中更易實現,也更穩定。
圖5顯示如何使用GMP對PA的輸入x和輸出y之間的關系進行建模。可以看到,該等式的三個單獨的求和塊彼此都非常相似。先來看看下方用紅色圈出來的第一個。|x(…)|k項是指輸入信號的包絡,其中k是多項式階。l將記憶集成到系統中。如果La={0,1,2},那么該模型允許輸出yGMP(n)由當前的輸入x(n)和過去輸入x(n – 1)和x(n – 2)決定。圖6分析多項式階k對樣本向量的影響。向量x是單個20 MHz載波,在復基帶上表示出來。去除記憶部分,以簡化GMP建模等式。x|x|k圖顯示的失真與圖4中的實際失真非常相似。
每個多項式階(k)和記憶延遲(l)都有相關的復值權重(akl)。在選擇模型的復雜程度之后(其中包括k和l的值),需要根據已知輸入信號的PA輸出實際觀測值來求解這些權重。圖7將簡化的等式轉換為矩陣形式。可以使用數學符號簡明表示該模型。但是,要在數字數據緩沖區實現DPD,用矩陣表示法會更簡單,也更具代表性。
來看看圖6中等式的第二行和第三行,為了簡化,這兩行被忽略了。注意,如果m設置為0,那么這兩行會變得與第一行一模一樣。這些行允許在包絡項和復基帶信號之間增加延遲(正延遲和負延遲)。這些稱為滯后交叉和超前交叉項,可以顯著提高DPD的建模精度。在嘗試對放大器的行為建模時,這些項提供了額外的自由度。注意,Mb、Mc、Kb和Kc不包含0;否則,會重復第一行的項。
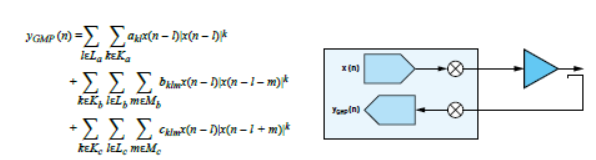
圖5:用于PA失真建模的GMP。
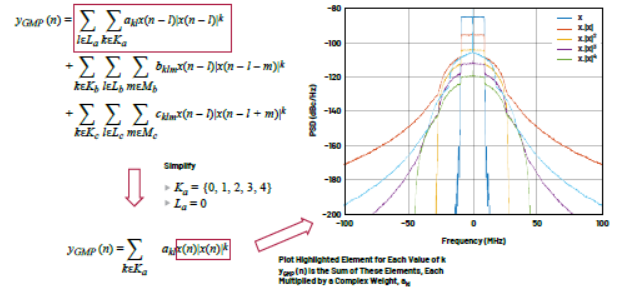
圖6:在信號x的頻域中,階(k)對信號的影響曲線圖。

圖7:將簡化的等式轉換為數據緩沖區的矩陣運算(更接近于數字實現方式)。
那么,如何確定模型的階、記憶項的數量,以及應該添加哪些交叉項?此時,就需要一定數量的“黑魔法”了。此時,有關失真的物理學知識能夠提供一定幫助。放大器的類型、制造材料,以及通過放大器的信號帶寬都會影響建模項,可以幫助熟悉該領域的工程師確定應該使用哪個模型。但是,除此之外,還涉及一定程度的反復試驗。
有了模型架構,從數學角度來解決該問題的最后一個方面是如何求解權重系數。在實際場景中,人們傾向于求解上述模型的倒數。事實證明,這些模型系數能夠彼此互惠,可以使用相同的權重對捕捉到的PA輸出向量進行后失真,以消除非線性,并對通過PA發送的發射信號預失真,使得PA輸出盡可能呈現線性。在圖8所示的框圖中,顯示了如何對權重系數進行估算和預失真。

圖8:建模和預失真間接實現框圖。
在逆模型中,將圖7給出的矩陣等式互換,給出X?= Yw。其中,矩陣Y的構成方式與其他示例中X的構成方式相同,如圖9所示。在本例中,包含了一個記憶項,且減少了包含的多項式的階數。為了求解w,我們需要得出Y的倒數。Y不是方形的(是一個瘦長矩陣),所以需要使用“偽逆”矩陣進行求解(參見等式1)。這是從最小二乘意義上求解w,最小化了X?和Yw之間的差的平方!

鑒于是在具有不同信號的真實環境中使用,可以對其進一步優化。在這里,系數是基于之前的值進行更新,因此受到限制。μ是0和1之間的常數值,用于控制每次迭代時權重的變化量。如果μ= 1,w0=0,那么此等式立即恢復到基本最小二乘解。如果將μ設為小于1的值,則需要多次迭代才能使系數收斂。
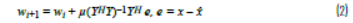
注意,這里描述的建模和估算技術并非是執行DPD的唯一方式。也可以使用其他技術,例如基于動態偏差減少的建模來代替或作為附加方法使用。上述用于求解系數的估算技術具有多種實現方式。鑒于篇幅,此處不再贅述。
如何在微處理器中實現這一技術?
前面介紹了相關數學知識。下一個問題是如何在實際通信系統中實現?在數字基帶中,一般在微處理器或FPGA中實現。目前,ADI的RadioVerse收發器產品(例如ADRV902x系列)內置微處理器內核,已經集成了這類算法,其結構有助于輕松實現DPD。不僅提供了高度集成的RF硬件,還為客戶提供可配置的軟件工具。
在嵌入式軟件中實現DPD涉及兩個方面。一是DPD執行器,對實時發送的數據執行實時預失真,二是DPD自適應引擎,基于觀察到的PA輸出來更新DPD系數。
對于如何在微處理器或類似器件中實時執行DPD和許多其他信號處理概念,關鍵在于使用查找表(LUT)。LUT允許用更簡單的矩陣索引操作來代替成本高昂的實時計算。來看看DPD執行器如何對發送的數據樣本進行預失真。代表符號如圖8所示,其中u(n)表示要傳輸的新數據樣本,x(n)表示預失真版本。圖10顯示在給定場景下,獲取一個預失真樣本所需的計算。這是一個相對受限的示例,最高多項式階為三階,只有一次記憶選取和一個交叉項。即使在這種情況下,要獲取這樣一個數據樣本,也需要進行大量乘法、冪運算和加法運算。
在這種情況下,使用LUT可以減輕實時計算負擔。可以將圖10所示的等式改寫成圖11所示的樣式,其中輸入LUT的數據會變得更加明顯。每個LUT都包含等式中突出顯示項的結果值,它們對應|u(n)|的多個可能值。分辨率取決于在可用硬件中實現的LUT大小。當前輸入樣本的幅度大小基于LUT的分辨率進行量化,可以作為索引,用于訪問給定輸入的正確LUT元素。
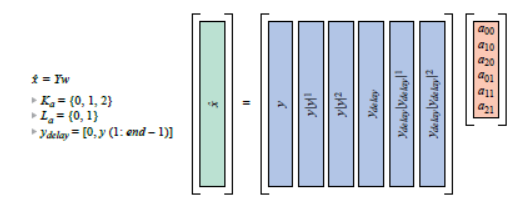
圖9:以矩陣形式表示的逆算法等式,有些記憶包含在其中。
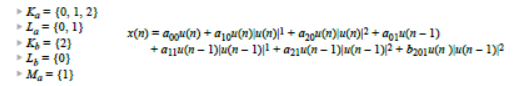
圖10:具有一次記憶選擇和一個三階交叉項元素的三階預失真計算案例。
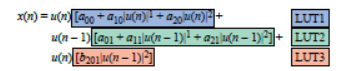
圖11:對等式項重新分組,以顯示LUT的結構。
圖12顯示如何將LUT集成到示例案例的完全預失真執行器實現方案。注意,這只是其中一種可能的實現方法。在保持相同輸出的情況下,可以做出更改,例如:可以將延遲元素z–1移動到LUT2右側。
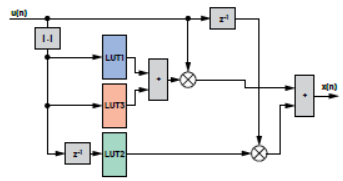
圖12:使用LUT可能實現DPD的框圖。
自適應引擎負責求解用于計算執行器中的LUT值的系數。這涉及到求解等式1和2中描述的w向量。偽逆矩陣運算(YHY)-1YH會耗費大量計算資源。等式1可以改寫為

如果CYY=YHY,CYx=YHx,等式3會變成

CYY是矩形矩陣,可以通過柯列斯基分解方法分解為上三角矩陣L和共軛轉置矩陣(CYY=LHL)的乘積。這樣我們可以通過引入一個虛擬變量z來求解w,求解方法如下:

然后,重新代入這個虛擬變量,求解

因為L和LH分別是上、下三角矩陣,所以花費很少的計算資源,就可以求解等式5和等式6,得出w。自適應引擎每次運行,得出w的新值時,都需要更新執行器LUT來體現這一點。根據觀察到的PA輸出,或者操作員掌握的待傳輸信號的變化情況,自適應引擎可以按照設定的定期間隔或不規則的間隔執行操作。
在嵌入式系統中實現DPD需要進行大量檢查和平衡,以確保系統的穩定性。最重要的是,發送數據緩沖器和捕捉緩沖器數據的時間要一致,以確保它們之間建立的數學關系是正確的,且在長時間之后仍然保持正確。如果這種一致性喪失,那么自適應引擎返回的系數將不能對系統執行正確的預失真,可能導致系統不穩定。還應檢查預失真執行器輸出,確保信號不會使DAC飽和。
審核編輯:劉清
-
功率放大器
+關注
關注
102文章
3599瀏覽量
132019 -
晶體管
+關注
關注
77文章
9706瀏覽量
138490 -
DPD
+關注
關注
3文章
40瀏覽量
15280 -
RF系統
+關注
關注
0文章
14瀏覽量
8454
原文標題:數字預失真技術的數學建模與物理實現
文章出處:【微信號:CloudBrain-TT,微信公眾號:云腦智庫】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
GC5322_DPD數據分析




 什么是DPD?為什么要使用DPD呢?
什么是DPD?為什么要使用DPD呢?











評論