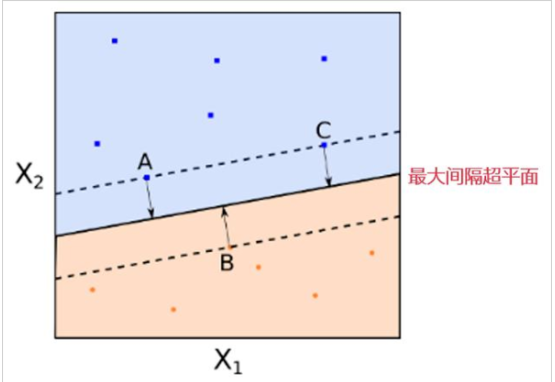
支持向量機尋找的最優分類直線應滿足如下條件:
(1)該直線可將訓練數據完全分為兩類。
(2)該直線可最大化間隔。
(3)該直線處于間隔的中間,其與所有支持向量(任意一條可將訓練樣本完全分類的直線分別向兩側被平行移動時,最先穿過的一個或幾個訓練樣本)的距離相等。
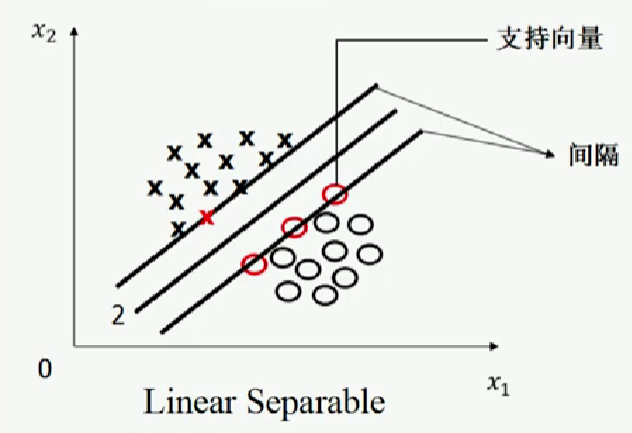
圖片來源:中國慕課大學《機器學習概論》
可推出支持向量機尋找最優分類超平面(超平面是將三維以上特征空間的訓練數據分割為不同類別的“圖形”)應滿足如下條件:
(1)該超平面可將訓練數據完全分為兩類。
(2)該超平面可最大化間隔。
(3)該超平面處于間隔的中間,其與所有支持向量的距離相等。
下文介紹通過數學方法,將支持向量機尋找線性可分訓練數據集的最優分類超平面的過程,描述為最優化問題。
回顧線性可分的定義:訓練樣本集 {(Xi,yi)}在i=1~N線性可分是指存在ω和b(Xi=[xi1,xi2,…,xin],ω=[ω1,ω2,…,ωn]T),使得對 i=1~N,有:
若yi=+1,則ωTXi+b>0;
若yi=-1,則ωTXi+b<0。
同時,基于以下兩個事實:
事實1:ωTx+b=0與(aωTx)+(ab)=0是同一個超平面(a≠0)。(此事實可基于二維特征空間的情況理解,當a≠0時,二維特征空間中,ωx+b=0與aωx+ab=0是同一條直線)
事實2:一個點X0到超平面ωTx+b=0的距離d的公式為:d=|ωTX0+b|/||ω||,其中||ω||2=ω12+ω22…+ωn2。(此事實也可基于二維特征空間的情況理解,二維特征空間中,一個點(x0,y0)到ω1x0+ω2y0+b=0的距離為:d=|ω1x0+ω2y0+b|/√(ω12+ω22),√代表根號)
因為ωTx+b=0與(aωTx)+(ab)=0是同一個超平面,所以可以通過縮放(即直線方程兩端均乘以相同系數),使得ωTx+b在支持向量x0上有|ωTx0+b|=1(根據線性可分的定義,支持向量x0上有|ωTx0+b|>0,假設|ωTx0+b|=0.5,那么可以通過將該方程兩端均乘以2縮放為|ωTx0+b|=1,其他情況均可以此類推)。
那么,根據事實2,支持向量x0到超平面的距離d=|ωTx0+b|/||ω||=1/||ω||。因此,最大化支持向量至超平面的距離(即最大化超平面的間隔)等價于最小化||ω||。
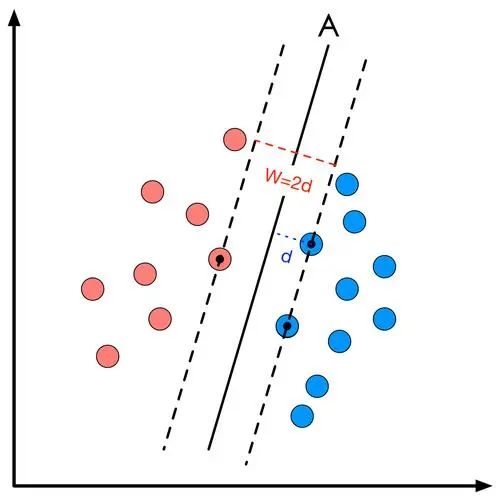
圖片來源:來自網絡
因此,支持向量機尋找線性可分訓練數據集的最優分類超平面的過程可描述為最小化1/2||ω||2(最小化1/2||ω||2即可使||ω||最小化)的最優化問題。
又因為非支持向量與超平面的距離大于支持向量與超平面的距離,所以非支持向量與超平面的距離d>1/||ω||,即在非支持向量x0上有|ωTx0+b|>1。
綜合支持向量與非支持向量距離取值,可得出支持向量機尋找線性可分訓練數據集的最優分類超平面的限制條件:yi(ωTXi+b)≥1,i=1~N。
綜上,在線性可分情況下,支持向量機尋找最佳超平面的優化問題可以表示為 :
最小化:1/2||ω||2,
限制條件:yi(ωTXi+b)≥1,i=1~N。
上述優化問題中,ω和b為待求量,(Xi,yi),i=1~N為已知量。該優化問題屬于凸優化問題(CONVEX OPTIMIZATION)。當一個問題轉化為凸優化問題時,該問題可使用機器學習算法的工具包求解。
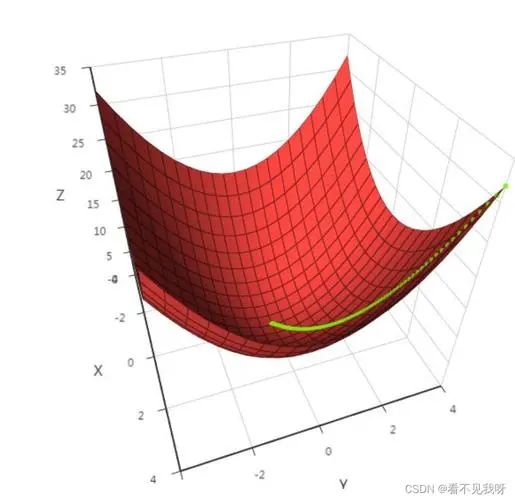
圖片來源:來自網絡
審核編輯:劉清
-
向量機
+關注
關注
0文章
166瀏覽量
21040 -
機器學習
+關注
關注
66文章
8467瀏覽量
133639
原文標題:機器學習相關介紹(8)——支持向量機(優化問題)
文章出處:【微信號:行業學習與研究,微信公眾號:行業學習與研究】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于多分類支持向量機的隱寫域盲檢測
多分類孿生支持向量機研究進展
支持向量機的故障預測模型
基于支持向量機的噪聲分類與補償
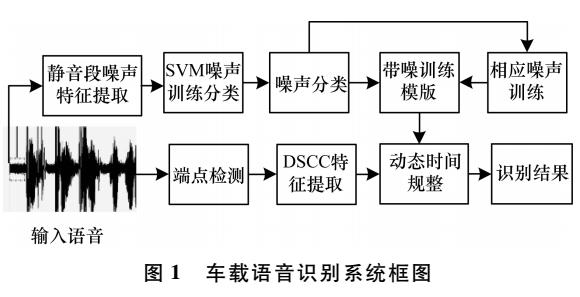
什么是支持向量機 什么是支持向量







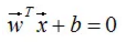













評論