相信很多人都知道Buck電路中輸入電容紋波電流有效值,在連續(xù)工作模式下可以用以下公式來計算:
然而,相信也有很多人并不一定知道上面的計算公式是如何推導(dǎo)出來的,下文將完成這一過程。
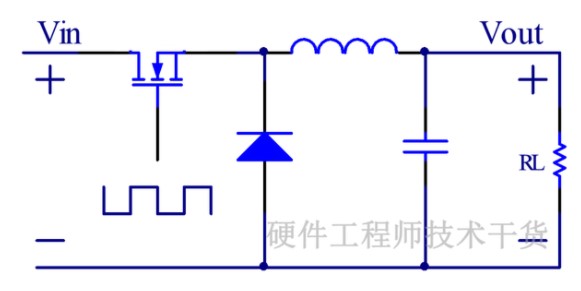
眾所周知,在BuckConverter電路中Q1的電流(IQ1)波形基本如圖1所示:0~DTs期間為一半梯形,DTs~Ts期間為零。當(dāng)0~DT期間Iq1 ⊿I足夠小時(不考慮輸出電流紋波的影響),則Iq1波形為近似為一個高為Io、寬為DTs的矩形,則有:
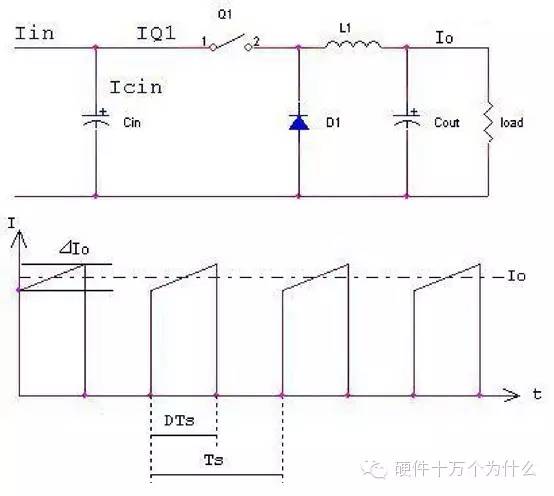
圖1
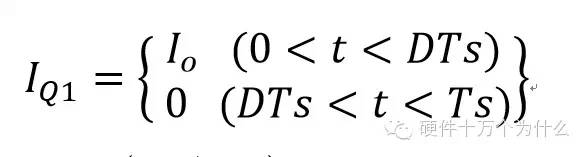
Iin=(Vo/Vin)*Io=DIo (Iin,只要Cin容量足夠大,則在整個周期中是基本恒定的;按照能量守恒定律:Pin≈Pout)
Icin=Iq1-Iin
對Icin 的表達(dá)式可以這樣理解:在Q1導(dǎo)通期間輸入端和輸入電容共同向輸出端提供電流,因此輸入電容電流等于Q1電流減去輸入端電流;在Q1關(guān)斷期間輸入端對電容充電,以補(bǔ)充在Q1導(dǎo)通期間所泄掉的電荷,而此時電流方向與所定義的正向是相反的,所以有Icin=-DIo根據(jù)有效值的定義.
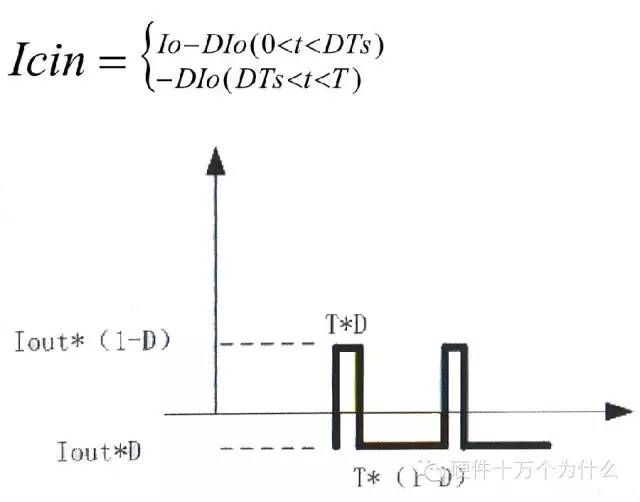

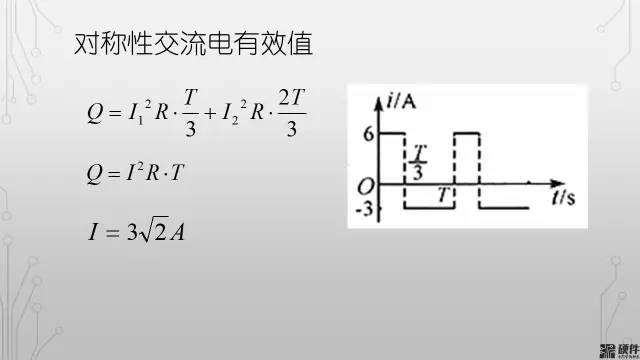
不難得出輸入電容的紋波電流有效值Icin.rms的計算公式:
有效值定義:有效值(Effectivevalue)在相同的電阻上分別通以直流電流和交流電流,經(jīng)過一個交流周期的時間,如果它們在電阻上所消耗的電能相等的話,則把該直流電流(電壓)的大小作為交流電流(電壓)的有效值,正弦電流(電壓)的有效值等于其最大值(幅值)的1/√2,約0.707倍。
在正弦交流電流電中根據(jù)熱等效原理,定義電流和電壓的有效值為其瞬時值在一個周期內(nèi)的方均根值。
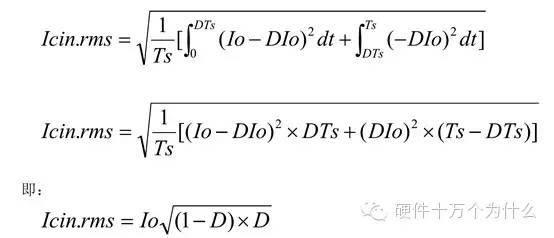
如果考慮輸出紋波ΔI,Icin.rms的電流有效值。
在忽略Buck電源的輸出電流紋波的前提下,進(jìn)行的近似計算。那么我們通過精確計算,可以得到一個更準(zhǔn)確的數(shù)據(jù)。
這個推導(dǎo)的過程,利用到積分公式。通過分析和推導(dǎo),可以對電路的工作原理有比較透徹的理解。
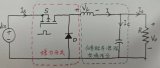
如果考慮輸出紋波電流。那么電容上的紋波電流的波形為:
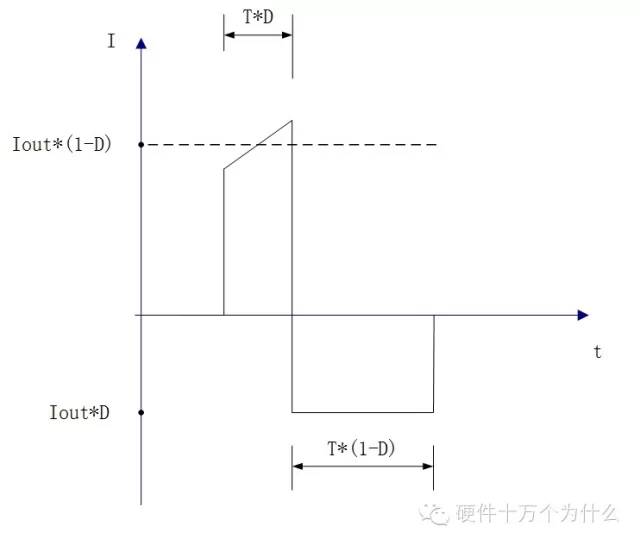
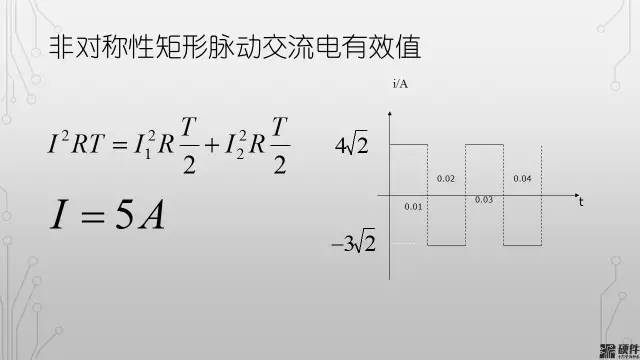
我們了解了脈沖波的有效電流的計算方法之后,我們知道開關(guān)電源的輸入電容承載的電流脈沖也是矩形脈沖電流
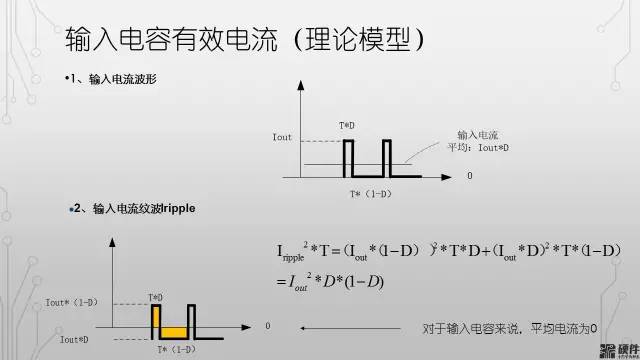
由于在上管打開的階段,輸入電流的大小即可近似的看成輸出電流的大小。所以只需要將輸出電流的波形疊加在輸入電容的波形上面,可以得到上圖中的波形。
那么按照有效電流定義,我們可以通過對電流平方在時間上的計算
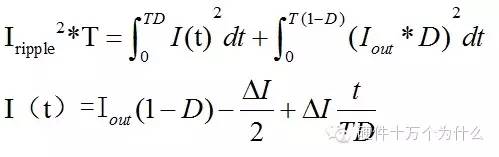
為了簡便計算,我們將能量拆成紋波部分,和直流部分。
原先的直流部分,我們直接用乘法進(jìn)行計算。
直流部分,我們按照近似計算的方法可以得到。
交流部分的功耗,我們按照公式計算可以得到:
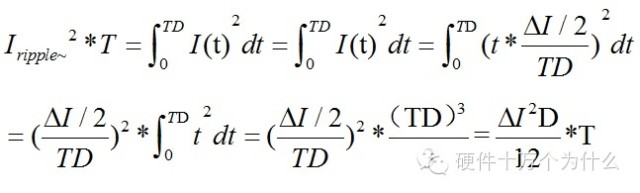
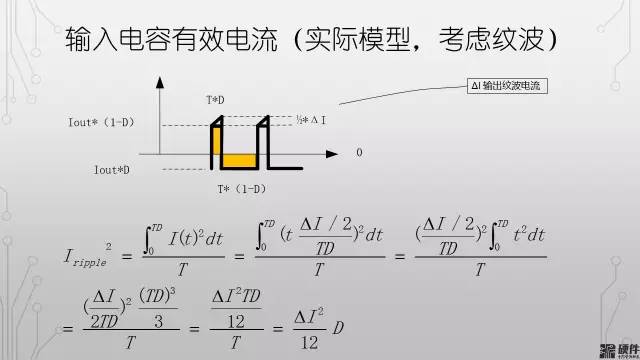
所以總的電容上的有效電流為:
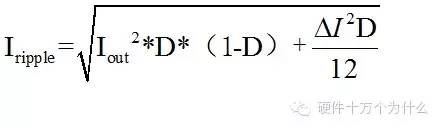
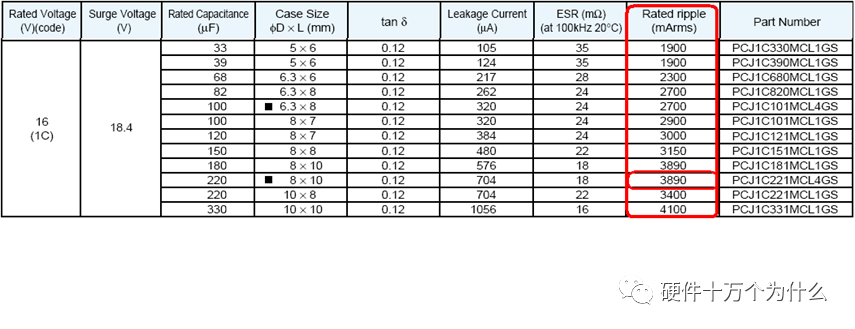
如果選用220uF的電容,每個能承受的有效電流為3.8A。。如果我們計算出來輸入電容的有效電流值為7A,則需要選用220uF電容2個。高分子電解電容能夠承受的有效電流值是有限的。在設(shè)計時需要充分考慮電容的承受能力。
如果沒有輸入電感,則電容的容值并不是非常重要,可以利用供電電源穩(wěn)定輸入電壓值。只要前一級的電源帶負(fù)載能力夠強(qiáng),應(yīng)對電流突變的能力足夠大(其實也是前一級的輸出電容足夠多),則電源輸入測的電容容量并不重要。
如果有輸入電感,則輸入端的電容容值顯得重要,影響輸入電壓值跌落和輸入電壓紋波,利用充放電的電量相同可得:
Q=C*ΔU
Q=IoutTD
C=IoutTD/ΔU
因為對于二次電源來說,下一級的輸入電容不夠,可以依賴別的同源的輸入電容,或者依賴上一級的輸出電容,來避免電源跌落。所以這個問題容易被我們忽視。
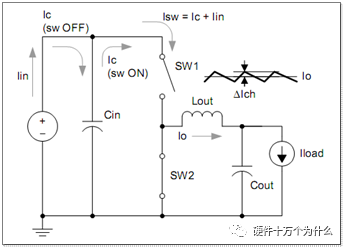
流過MOSFET的電流Isw是不連續(xù),輸入電容的作用是用來提供一個低阻抗的電流源來提供MOSFET電流。
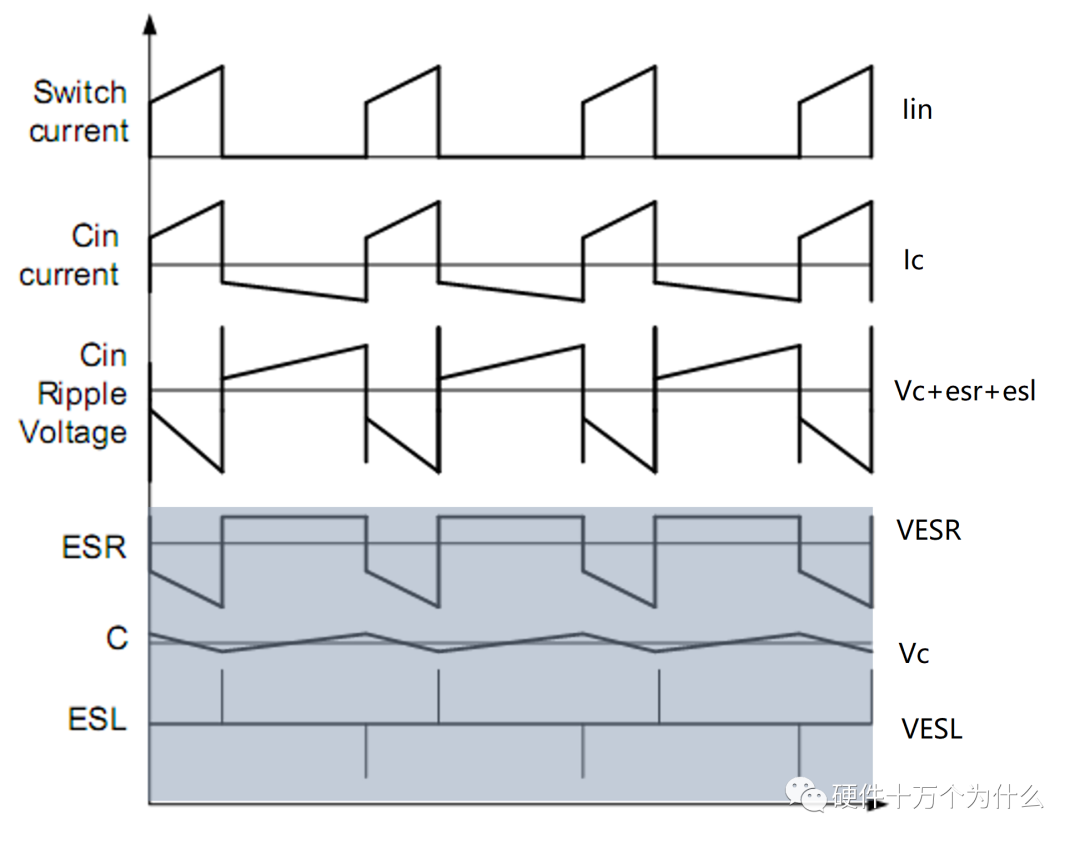
輸入電容上各電壓分量和電流波形
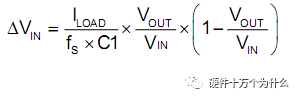
有些Datasheet會給一個上面的公式,讓你去計算電容容值的最小值。但是沒有給出為什么。或者直接給一個參考電路,告訴你:至少放兩個10uF的陶瓷電容,或者放置3顆100uF鋁電解電容等等。


當(dāng)上管關(guān)閉的時候,只是輸入電流給電容充電。此時Iin=Ic(sw OFF)
當(dāng)上管打開的時候,電容放電和輸入電流同時給輸出端供電。
此時,上管上的電流Isw=Ic(sw ON)+Iin
Isw≈Iout
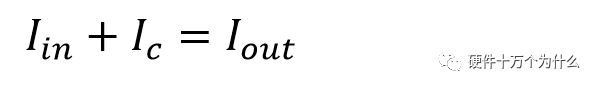
首先我們可以根據(jù)電容的:


可以得出:
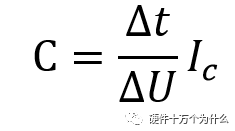
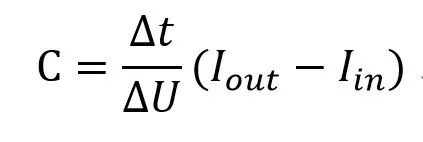
我們想知道一個周期內(nèi)電壓跌落多少:
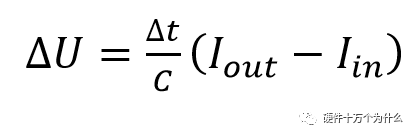
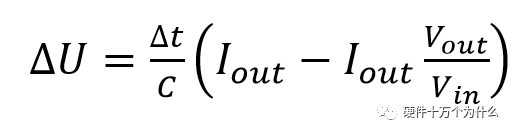
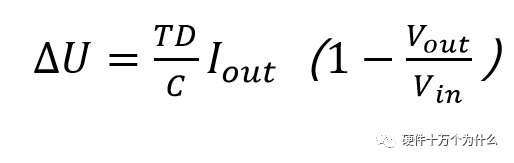
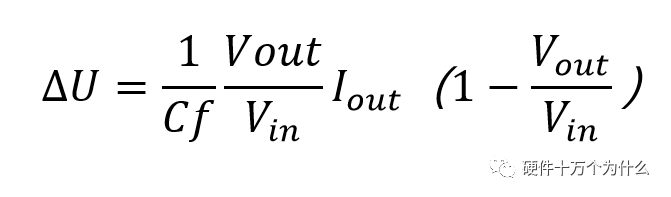
由紋波可見,需要在滿足電容容量的前提下,選用低ESR的陶瓷電容,同時需要減小ESL。
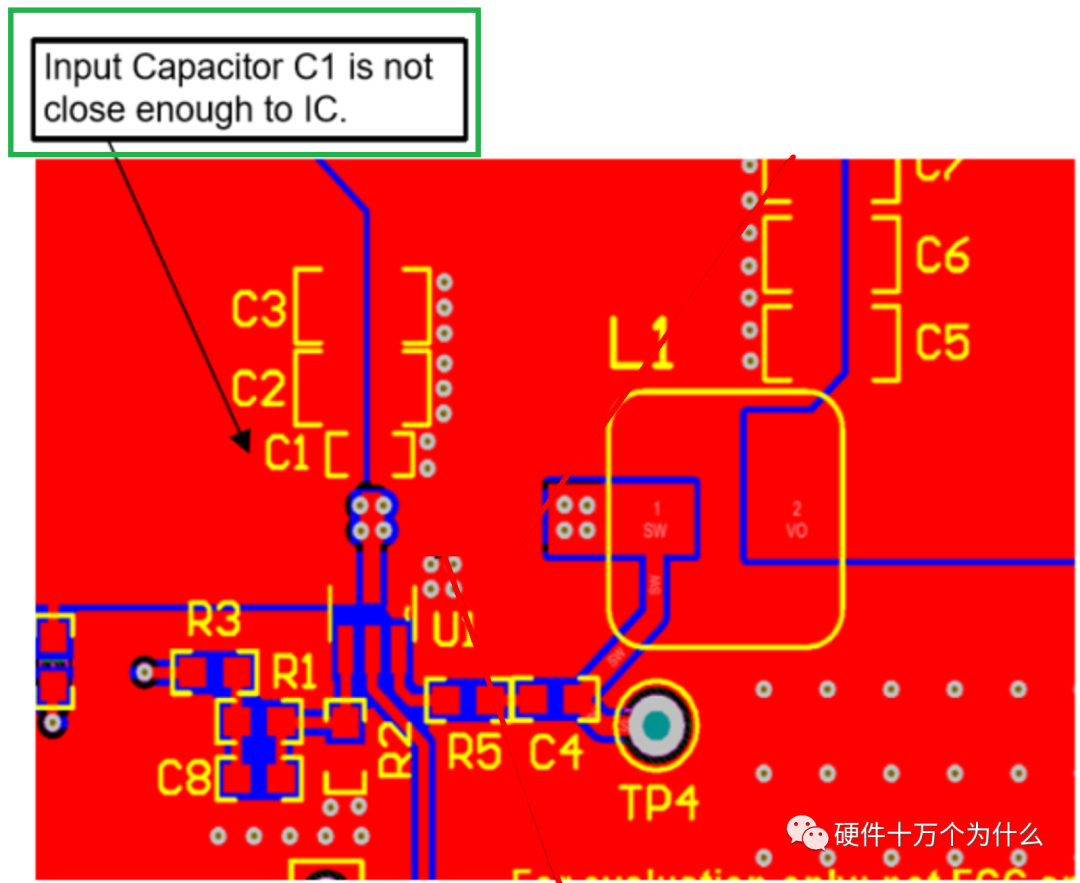
電容上本身的ESL并不大,但是經(jīng)常會有因為輸入電容較遠(yuǎn)或者地線較遠(yuǎn)引入較大的ESL在輸入端引起較大的尖峰,導(dǎo)致芯片供電異常或者芯片MOSFET過壓擊穿。
所以輸入電容的PCB布放,需要靠近輸入端的兩個管腳。
-
電流
+關(guān)注
關(guān)注
40文章
7085瀏覽量
133654 -
輸入電容
+關(guān)注
關(guān)注
1文章
46瀏覽量
9927 -
buck電路
+關(guān)注
關(guān)注
28文章
487瀏覽量
47097
發(fā)布評論請先 登錄
相關(guān)推薦
DCDC拓?fù)浣Y(jié)構(gòu)之BUCK電路
Buck電路中輸入電容紋波電流有效值計算
細(xì)說Buck的Boot電容(自舉電容)
開關(guān)電源設(shè)計之Buck電路電感、電容值的選取
DCDC之Buck電路電感、電容值的選取及分析
【設(shè)計技巧】電源設(shè)計必知電路之BUCK電路
開關(guān)電源之BUCK電路








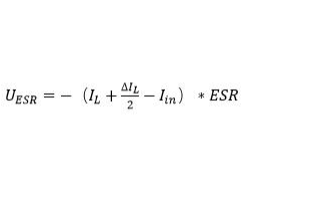











評論