PART1. 進位計數制
數制也稱計數制,是指用一組固定的符號和統一的規則來表示數值的方法。它按進位的原則進行計數的方法,稱為進位計數制。
PART2. 常用進位制
01 十進制
有10個基數:0 ~~ 9 ,逢十進一;
舉例說明:如1234=1*103+2*102+3*101+4*100,逢十進一,那么基數為10,單個數是0-9,每位的系數乘于基數(10)的N次方,N為其所處的位數。
02 二進制
有2 個基數:0 ~~ 1 ,逢二進一;
舉例說明:如1101=1*23+1*22+0*21+1*20=13,逢二進一,那么基數為2,單個數只有0和1, 每位的系數乘于基數(10)的N次方,N為其所處的位數。從第3位至0分別為8,4,2,1,所以二進制也成8421碼。如果表示有符號數,則用最高位表示符號,0為正數1為負數。正數以二進制原碼表示;負數則以補碼存儲,即將原碼逐位取反再加1。
03 八進制
有8個基數:0 ~~ 7 ,逢八進一;在PLC中常用于編址,數據運算應用較少。
04 十六進制
有16個基數:0 ~~ 9、A、B、C、D、E、F (A=10,B=11,C=12,D=13,E=14,F=15) ,逢十六進一。
PART3. 基數與位權
"基數"和"位權"是進位計數制的兩個要素。
01 基數
所謂基數,就是進位計數制的每位數上可能有的數碼的個數。例如,十進制數每位上的數碼,有"0"、"1"、"3",…,"9"十個數碼,所以基數為10。
02 位權
所謂位權,是指一個數值的每一位上的數字的權值的大小。例如十進制數4567從低位到高位的位權分別為100、101、102、103。因為:4567=4x103+5x 102+6x 101 +7x100
03 數的位權
任何一種數制的數都可以表示成按位權展開的多項式之和。比如:十進制數的435.05可表示為:435.05=4x102+3x 101+5x100+0x10-1 +5x 10-2 。位權表示法的特點:每一項=某位上的數字X基數的若干冪次;而冪次的大小由該數字所在的位置決定。
PART4. 十進制轉二進制
十進制數除2取余法,即十進制數除2,余數為權位上的數,得到的商值繼續除2,依此步驟繼續向下運算直到商為0為止。如圖:
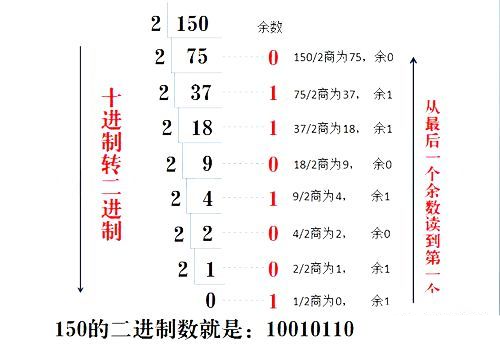
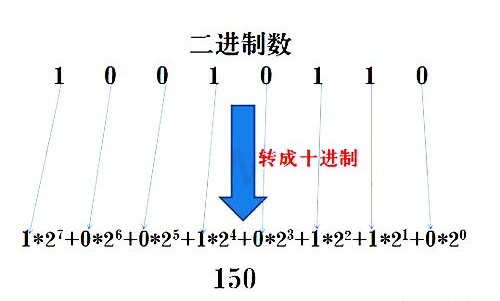
PART5. 二進制轉十進制
把二進制數按權展開、相加即得十進制數。如圖:
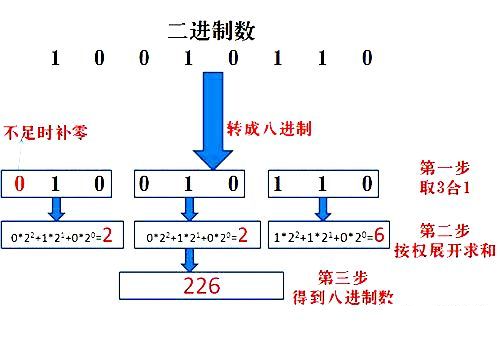
PART6. 二進制轉八進制
3位二進制數按權展開相加得到1位八進制數。注:3位二進制轉成八進制是從右到左開始轉換,不足時補0。如圖:
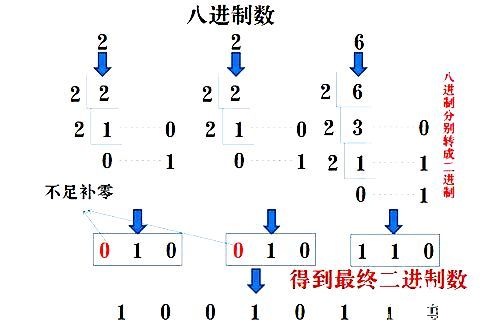
PART7. 八進制轉二進制
八進制數通過除2取余法,得到二進制數,對每個八進制為3個二進制,不足時在最左邊補零。如圖:
PART8. 二進制轉十六進制
與二進制轉八進制方法近似,八進制是取三合一,十六進制是取四合一。(注意事項,4位二進制轉成十六進制是從右到左開始轉換,不足時補0)。如圖:
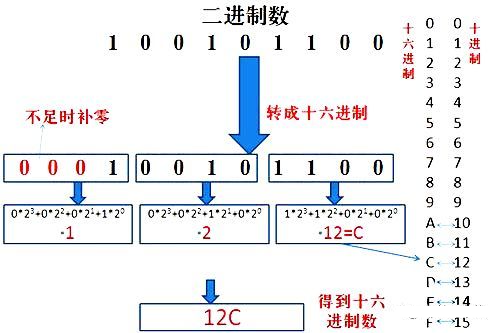
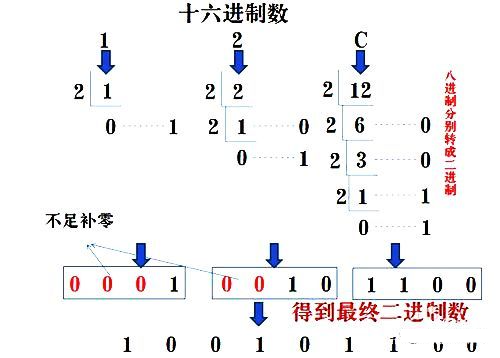
PART9. 十六制轉二進制
十六進制數通過除2取余法,得到二進制數,對每個十六進制為4個二進制,不足時在最左邊補零。如圖:
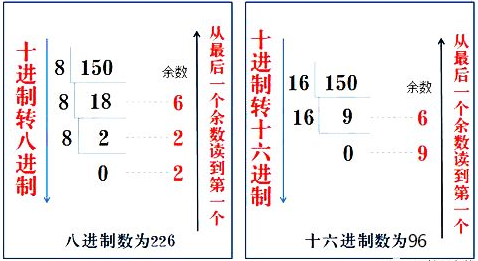
PART10. 十進制轉八進制或者十六進制
第一:間接法—把十進制轉成二進制,然后再由二進制轉成八進制或者十六進制。這里不再做圖片用法解釋。
第二:直接法—把十進制轉八進制或者十六進制按照除8或者16取余,直到商為0為止。(具體用法如下圖)
PART11. 八進制或者十六進制轉成十進制
把八進制、十六進制數按權展開、相加即得十進制數。(具體用法如下圖)

PART12. BCD碼轉十進制
BCD碼是用四位二進制表示一位十進制數,所以轉換方法類似二進制轉十六進制“取四合一”法,四位組合后轉成十進制得到的就是十進制。
以上就是PLC中常用進制及相互轉換方法,加上舉例是不是很簡單呢?
審核編輯:湯梓紅
-
plc
+關注
關注
5013文章
13331瀏覽量
464155 -
存儲
+關注
關注
13文章
4332瀏覽量
85956 -
二進制
+關注
關注
2文章
795瀏覽量
41692 -
十進制
+關注
關注
0文章
67瀏覽量
13240 -
八進制
+關注
關注
0文章
13瀏覽量
6556
原文標題:新手入門必看,PLC進位計數轉換方法
文章出處:【微信號:指南車機器人科技,微信公眾號:指南車機器人科技】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
labview中浮點數與十六進制字符串相互轉化
字符 數字相互轉換
labview里單精度浮點數和十六進制數如何相互轉換?
BCD碼與十進制數相互轉換,無密碼,可直接用
觸發器的相互轉換
PLC中常用數制及如何轉換





 PLC中常用進制及相互轉換方法
PLC中常用進制及相互轉換方法
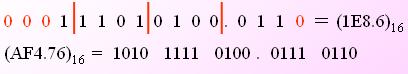











評論