麥克斯韋方程組是一組描述電場、磁場與電荷密度、電流密度之間關系的偏微分方程。它由四個方程組成:描述電荷如何產生電場的高斯定律、論述磁單極子不存在的高斯磁定律、描述電流和時變電場怎樣產生磁場的麥克斯韋-安培定律、描述時變磁場如何產生電場的法拉第感應定律。四個方程中,兩個方程涉及到散度,另外兩個方程涉及到旋度。散度和旋度是對向量場進行微分運算的兩種方式,它們可以用來刻畫向量場的性質。那么,散度和旋度具體有什么物理意義呢?
散度
散度是一個標量,它表示一個向量場在某一點處的發散程度。如果一個向量場在某一點處的散度為正,那么說明該點附近有向量從內部向外部發散;如果為負,那么說明有向量從外部向內部匯聚;如果為零,那么說明該點附近向量場沒有發散或收斂的趨勢。散度的物理意義是,如果在一個向量場中取一個小閉合曲面,那么該曲面上的向量通量與曲面包圍的體積成正比。
在麥克斯韋方程組中,高斯定律和高斯磁定律都涉及到了散度。高斯定律可以表示成如下形式:??E=ρ/ε_0。其中?·表示散度運算,E表示電場強度,ρ表示電荷密度,ε_0表示真空中的介電常數。這個方程告訴我們,電場在某一點處的散度等于該點處單位體積內的凈電荷除以真空介電常數。也就是說,電荷是產生電場散度的源頭。如果某一點處有正電荷,那么該點處的電場散度為正,說明有電場線從該點向外發散;如果有負電荷,那么該點處的電場散度為負,說明有電場線從外部向該點匯聚;如果沒有凈電荷,那么該點處的電場散度為零,說明該點附近電場沒有發散或收斂的趨勢。
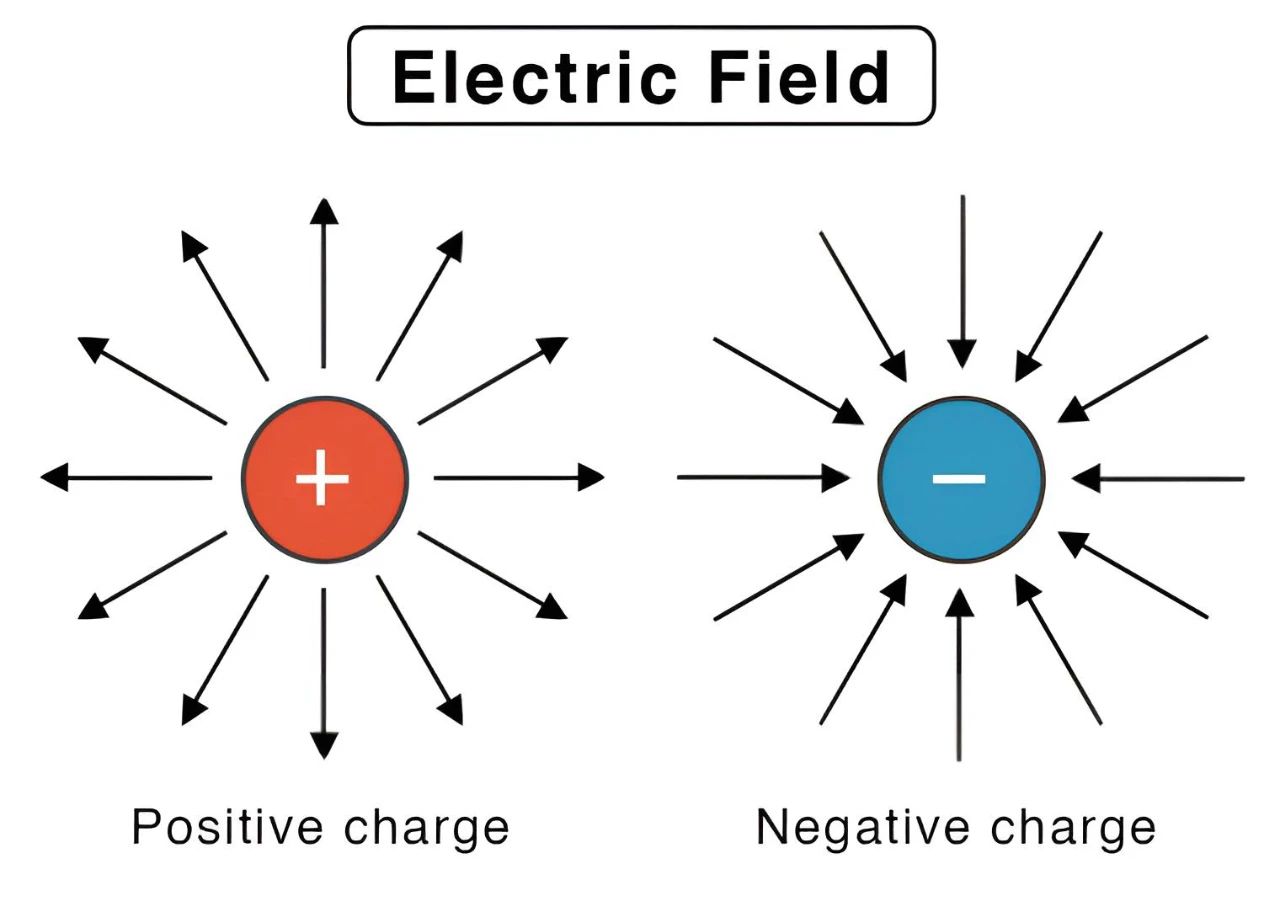
另一方面,高斯磁定律可以寫成如下的微分形式:??B=0。其中B表示磁場強度。這個方程告訴我們,磁場在某一點處的散度等于零,也就是說,該點附近沒有磁荷或磁單極子。如果某一點處有磁荷,那么該點處的磁場散度不為零,說明有磁場線從該點向外發散或從外部向該點收斂。但是,目前還沒有發現任何證據表明磁單極子的存在,因此高斯磁定律是一個普遍成立的定律。
旋度
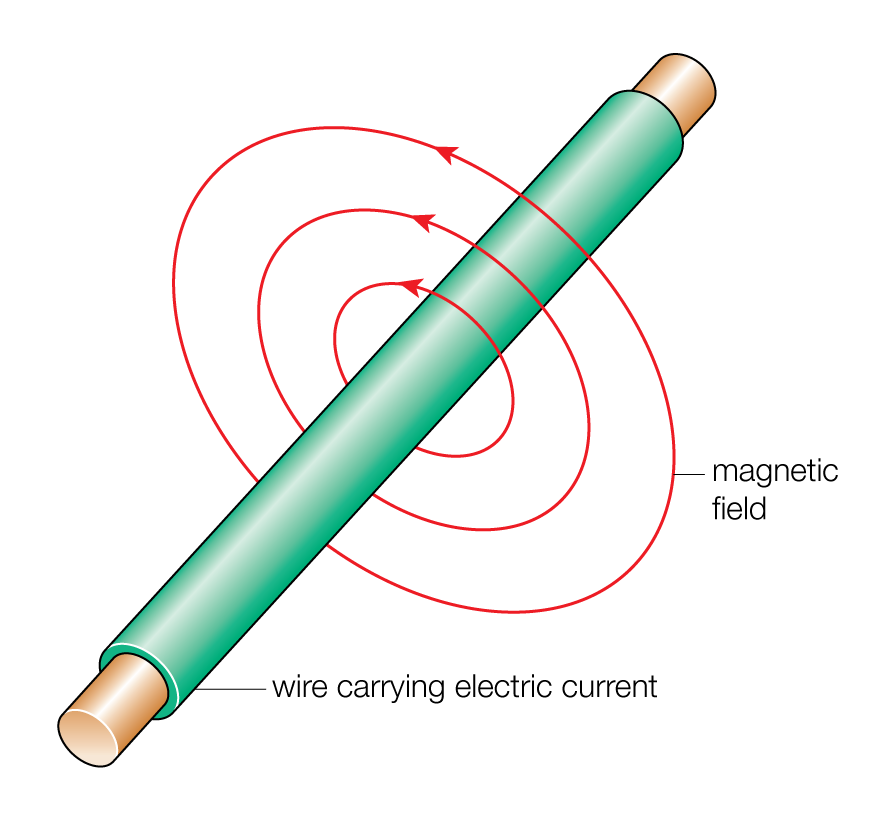
旋度是一個向量,它表示一個向量場在某一點處的旋轉程度。旋度的物理意義是,如果在一個向量場中取一個小閉合回路,那么該回路上的向量環流與回路包圍的面積成正比。旋度的方向由右手定則確定,即如果右手四指沿著回路方向彎曲,那么大拇指指向的方向就是旋度的方向。如果旋度不為零,表示向量場在該點有旋轉性;如果旋度為零,表示向量場在該點無旋轉性。法拉第感應定律可以寫成?×E=??B/?t,其中?×表示旋度運算。它告訴我們,當一個閉合回路在一個變化的磁場中時,會在回路上感應出一個電動勢,從而產生電流。這個電動勢的大小等于回路包圍的面積內磁通量的變化率的負值。
從公式可以看出,感應電場是一個旋轉性的場,它的旋度方向垂直于磁通量的變化方向。這樣,我們就可以用右手定則來判斷感應電流的方向:如果右手大拇指指向磁通量增加的方向,那么右手四指彎曲的方向就是感應電流的方向。同樣地,麥克斯韋-安培定律可以表示為:?×B=μ_0(J+ε_0?E/?t),它告訴我們,當一個閉合回路在一個變化的電場中時,會在回路上產生一個磁動勢,從而形成磁場。從公式我們可以看出,產生磁場的原因有兩個:一是電流,二是變化的電場。這兩個因素都會使得磁場具有旋轉性,它們的旋度方向垂直于電流或電場矢量的變化方向。這樣,我們也可以用右手定則來判斷磁場線的方向:如果右手四指指向電流或電位移矢量增加的方向,那么右手大拇指指向的方向就是磁場線的方向。
通過以上分析,我們可以發現,散度和旋度是描述電磁場分布和變化的兩個重要工具。散度反映了電荷或磁單極子(如果存在)對電場或磁場的影響;旋度反映了時變電場或時變磁場對彼此產生影響的方式。麥克斯韋方程組用散度和旋度將四個基本定律統一起來,揭示了電磁現象背后的普遍規律。
編輯:黃飛
-
磁場
+關注
關注
3文章
900瀏覽量
24561 -
電磁場
+關注
關注
0文章
797瀏覽量
47744 -
麥克斯韋方程組
+關注
關注
0文章
14瀏覽量
9738
原文標題:散度和旋度:理解麥克斯韋方程組的兩個關鍵工具
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
麥克斯韋方程組究竟帶來了什么
麥克斯韋Maxwell方程組是怎么來的
淺析麥克斯韋方程組
電與磁的開始麥克斯韋方程組到追逐電磁波
電磁場理論之麥克斯韋方程組論文的詳細資料免費下載
追逐麥克斯韋方程組與電磁波理論
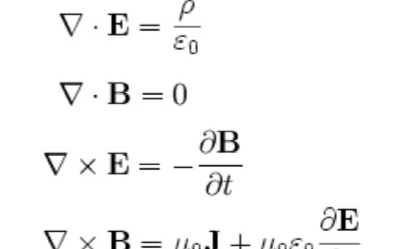
麥克斯韋方程組的詳細資料說明

電磁波究竟是如何傳播的?一文帶你搞懂麥克斯韋方程組
電磁波的傳播原理和麥克斯韋方程組的詳細說明
射頻微波設計入門——麥克斯韋方程組
描述電磁場的麥克斯韋方程組
聊聊介電常數那些事
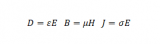







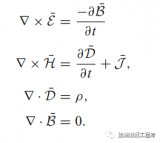











評論