單調棧實際上就是棧，只是利用了一些巧妙的邏輯，使得 每次新元素入棧后，棧內的元素都保持有序 （單調遞增或單調遞減）。

本文就通過幾道算法題來看看單調棧模板的使用。

單調棧模板

首先，看一下 Next Greater Number 的原始問題，這是力扣第 496 題「下一個更大元素 I」：

給你一個數組，返回一個等長的數組，對應索引存儲著下一個更大元素，如果沒有更大的元素，就存 -1。

函數簽名如下：

vector<int> nextGreaterElement(vector<int>& nums);

比如說，輸入一個數組nums = [2,1,2,4,3]，你返回數組[4,2,4,-1,-1]。

解釋：第一個 2 后面比 2 大的數是 4; 1 后面比 1 大的數是 2；第二個 2 后面比 2 大的數是 4; 4 后面沒有比 4 大的數，填 -1；3 后面沒有比 3 大的數，填 -1。

這道題的暴力解法很好想到，就是對每個元素后面都進行掃描，找到第一個更大的元素就行了。但是暴力解法的時間復雜度是O(n^2)。

這個問題可以這樣抽象思考：把數組的元素想象成并列站立的人，元素大小想象成人的身高。這些人面對你站成一列，如何求元素「2」的 Next Greater Number 呢？很簡單，如果能夠看到元素「2」，那么他后面可見的第一個人就是「2」的 Next Greater Number，因為比「2」小的元素身高不夠，都被「2」擋住了，第一個露出來的就是答案。

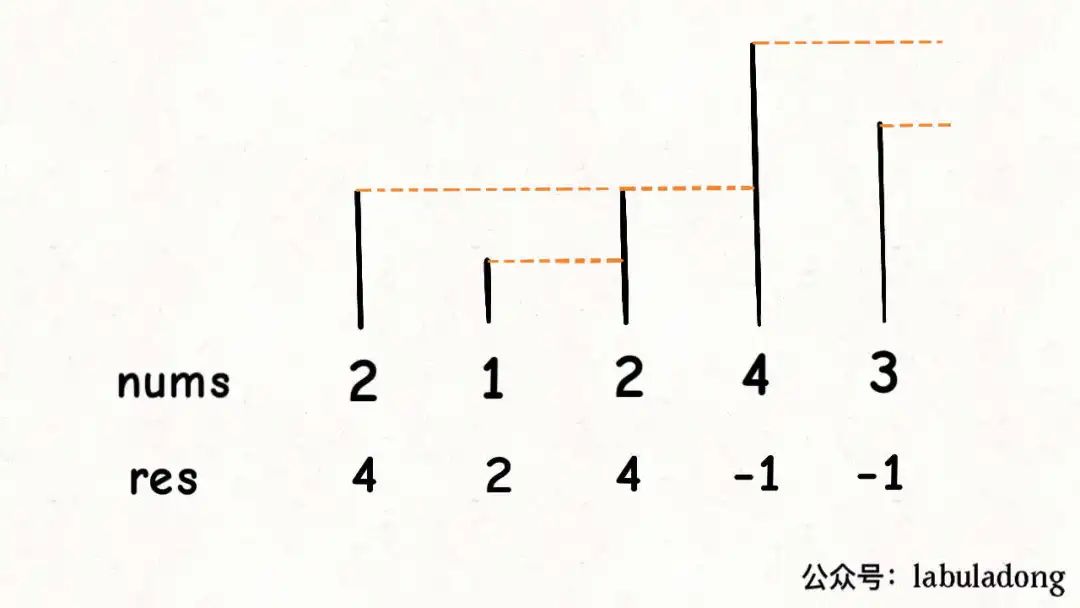
這個情景很好理解吧？帶著這個抽象的情景，先來看下代碼。

vector<int> nextGreaterElement(vector<int>& nums) {
    vector<int> res(nums.size()); // 存放答案的數組
    stack<int> s;
    // 倒著往棧里放
    for (int i = nums.size() - 1; i >= 0; i--) {
        // 判定個子高矮
        while (!s.empty() && s.top() <= nums[i]) {
            // 矮個起開，反正也被擋著了。。。
            s.pop();
        }
        // nums[i] 身后的 next great number
        res[i] = s.empty() ? -1 : s.top();
        // 
        s.push(nums[i]);
    }
    return res;
}

這就是單調隊列解決問題的模板。for 循環要從后往前掃描元素，因為我們借助的是棧的結構，倒著入棧，其實是正著出棧。while 循環是把兩個「個子高」元素之間的元素排除，因為他們的存在沒有意義，前面擋著個「更高」的元素，所以他們不可能被作為后續進來的元素的 Next Great Number 了。

這個算法的時間復雜度不是那么直觀，如果你看到 for 循環嵌套 while 循環，可能認為這個算法的復雜度也是O(n^2)，但是實際上這個算法的復雜度只有O(n)。

分析它的時間復雜度，要從整體來看：總共有n個元素，每個元素都被push入棧了一次，而最多會被pop一次，沒有任何冗余操作。所以總的計算規模是和元素規模n成正比的，也就是O(n)的復雜度。

問題變形

單調棧的使用技巧差不多了，來一個簡單的變形，力扣第 1118 題「一月有多少天」：

給你一個數組T，這個數組存放的是近幾天的天氣氣溫，你返回一個等長的數組，計算： 對于每一天，你還要至少等多少天才能等到一個更暖和的氣溫；如果等不到那一天，填 0 。

函數簽名如下：

vector<int> dailyTemperatures(vector<int>& T);

比如說給你輸入T = [73,74,75,71,69,76]，你返回[1,1,3,2,1,0]。

解釋：第一天 73 華氏度，第二天 74 華氏度，比 73 大，所以對于第一天，只要等一天就能等到一個更暖和的氣溫，后面的同理。

這個問題本質上也是找 Next Greater Number，只不過現在不是問你 Next Greater Number 是多少，而是問你當前距離 Next Greater Number 的距離而已。

相同的思路，直接調用單調棧的算法模板，稍作改動就可以，直接上代碼吧：

vector<int> dailyTemperatures(vector<int>& T) {
    vector<int> res(T.size());
    // 這里放元素索引，而不是元素
    stack<int> s; 
    /* 單調棧模板 */
    for (int i = T.size() - 1; i >= 0; i--) {
        while (!s.empty() && T[s.top()] <= T[i]) {
            s.pop();
        }
        // 得到索引間距
        res[i] = s.empty() ? 0 : (s.top() - i); 
        // 將索引入棧，而不是元素
        s.push(i); 
    }
    return res;
}

單調棧講解完畢，下面開始另一個重點：如何處理「循環數組」。

如何處理環形數組

同樣是 Next Greater Number，現在假設給你的數組是個環形的，如何處理？力扣第 503 題「下一個更大元素 II」就是這個問題：

比如輸入一個數組[2,1,2,4,3]，你返回數組[4,2,4,-1,4]。擁有了環形屬性， 最后一個元素 3 繞了一圈后找到了比自己大的元素 4 。

一般是通過 % 運算符求模（余數），來獲得環形特效：

int[] arr = {1,2,3,4,5};
int n = arr.length, index = 0;
while (true) {
    print(arr[index % n]);
    index++;
}

這個問題肯定還是要用單調棧的解題模板，但難點在于，比如輸入是[2,1,2,4,3]，對于最后一個元素 3，如何找到元素 4 作為 Next Greater Number。

對于這種需求，常用套路就是將數組長度翻倍 ：

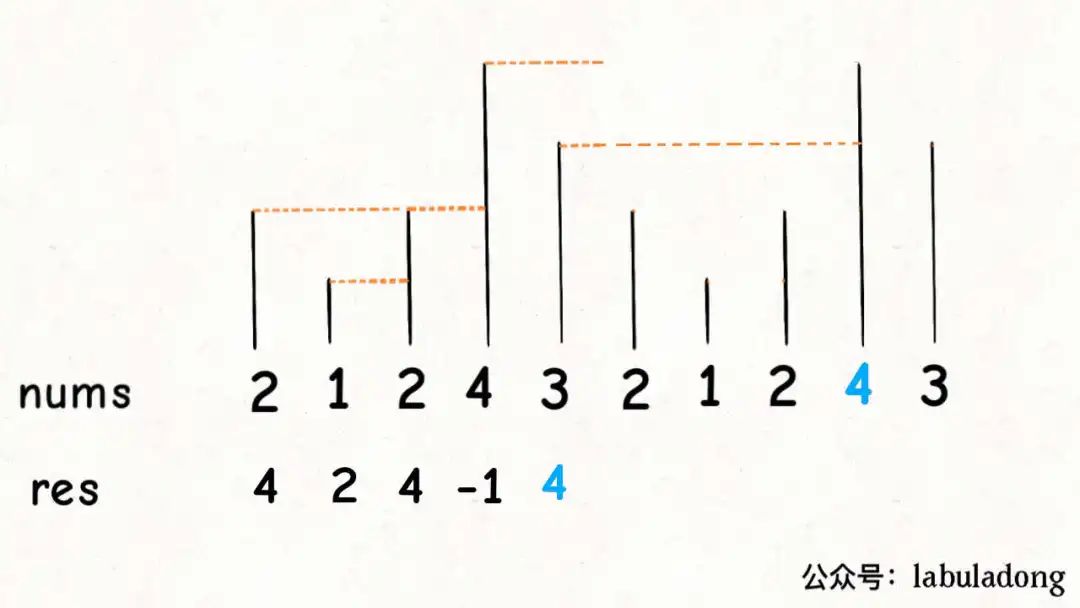
這樣，元素 3 就可以找到元素 4 作為 Next Greater Number 了，而且其他的元素都可以被正確地計算。

有了思路，最簡單的實現方式當然可以把這個雙倍長度的數組構造出來，然后套用算法模板。但是， 我們可以不用構造新數組，而是利用循環數組的技巧來模擬數組長度翻倍的效果 。

直接看代碼吧：

vector<int> nextGreaterElements(vector<int>& nums) {
    int n = nums.size();
    vector<int> res(n);
    stack<int> s;
    // 假裝這個數組長度翻倍了
    for (int i = 2 * n - 1; i >= 0; i--) {
        // 索引要求模，其他的和模板一樣
        while (!s.empty() && s.top() <= nums[i % n])
            s.pop();
        res[i % n] = s.empty() ? -1 : s.top();
        s.push(nums[i % n]);
    }
    return res;
}

這樣，就可以巧妙解決環形數組的問題，時間復雜度O(N)。