什么是振蕩器?

振蕩器是一種機械或電子結構，它根據幾個變量產生振蕩。我們都有需要振蕩器的設備， 我們家里的傳統時鐘作為掛鐘或手表，各種類型的金屬探測器，涉及微控制器和微處理器的計算機都使用振蕩器，尤其是產生周期信號的電子振蕩器。基于那里的配置有許多類型的振蕩器，如 Hartley 振蕩器、Colpitts 振蕩器、Wein橋振蕩器、石英晶體振蕩器、相移振蕩器電路等。

RC 振蕩器和相位：

當我們討論 RC 振蕩器時，由于它也被稱為相移振蕩器，我們需要對 什么是相位有一個公平的理解。看這張圖片：

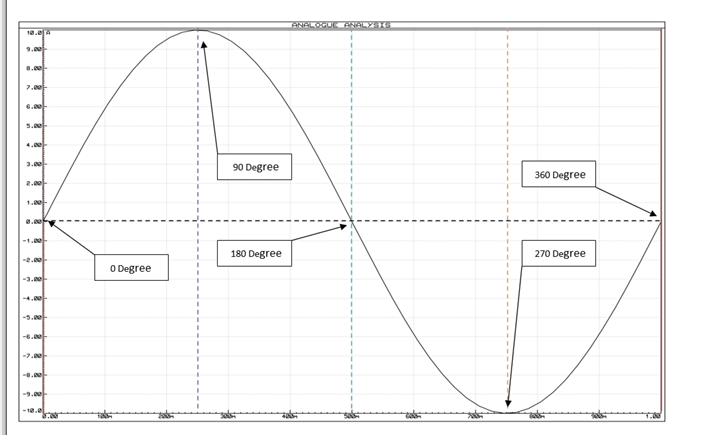
如果我們看到上面 這樣的正弦波，我們會清楚地看到信號的起點是0度相位，之后信號的每個峰值點從正到0再到負點再到0分別表示為90度、180 度、270 度和 360 度相位。

相位是正弦波在 360 度參考中的完整周期。

事不宜遲，讓我們看看 相移是什么?

如果我們移動正弦波起點而不是 0 度，相位就會移動。我們將在下一張圖片中了解相移。

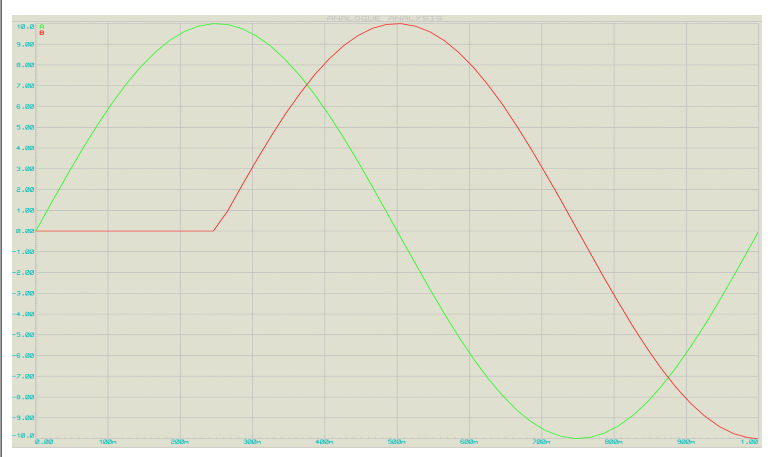
在這張圖片中，有兩個交流正弦信號波，第一個綠色正弦波的相位是 360 度，而紅色正弦波是第一個的復制品，讀取信號與綠色信號的相位相差 90 度。

使用 RC 振蕩器，我們可以改變正弦信號的相位。

使用 RC 振蕩器電路的相移：

RC 代表 電阻器和電容器 。我們可以僅使用一個電阻和一個電容器的形式來簡單地形成相移電阻-電容網絡。

正如在 高通濾波器教程中看到的，同樣的電路適用于這里。典型 的 RC 移相振蕩器 可以由串聯的電容器和并聯的電阻器產生。

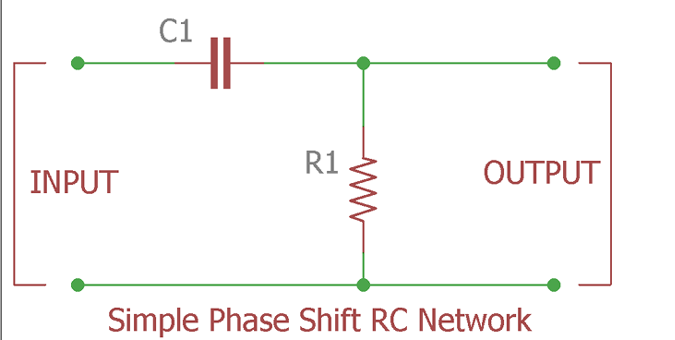
這是一個 單極移相網絡 ;該電路與無源高通濾波器相同 。理論上，如果 我們在這個 RC 網絡上應用同相信號，輸出相位將正好偏移 90 度 . 但如果我們在現實中嘗試并檢查相移，那么我們將實現 60 度到小于 90 度的相移。這取決于頻率，以及在現實中產生不利影響的元件容差。眾所周知，沒有什么是完美的，所謂的實際值或預期值與現實之間應該存在一些差異。溫度和其他外部依賴性導致難以實現精確的 90 度相移，一般為 45 度，60 度通常取決于頻率，而在許多情況下實現 90 度是一項非常困難的工作。

該高通濾波器的電路以及組件值如下圖所示：-

這是我們在之前的無源高通濾波器教程中使用的示例 。它將產生 4.9 KHz 的帶寬。如果我們檢查拐角頻率，我們將確定振蕩器輸出端的相位角。

現在我們可以看到相移從 90 度開始，這是 RC 振蕩器網絡的最大相移，但在拐角頻率點，相移為 45 度。

現在考慮到相移為 90 度的事實，或者如果我們選擇振蕩器電路結構，如將產生 90 度相移的特殊方式，那么由于頻率穩定因素較差，電路將失去其邊界范圍內的免疫力。正如我們可以想象的那樣，在曲線剛開始的 90 度點，從 10Hz 或更低到 100Hz 幾乎是平坦的。這意味著如果振蕩器的頻率由于元件容差、溫度和其他不可避免的情況而略有變化，相移將不會改變。那不是一個好的選擇。所以我們認為 60 度或 45 度是單極 RC 網絡振蕩器可接受的相移 。頻率穩定性將提高。

級聯多個 RC 濾波器：

級聯三個 RC 濾波器：

考慮到我們不能只實現 60 度相移而不是 90 度這一事實，我們可以級聯三個 RC 濾波器(如果 RC 振蕩器的相移為 60 度)或串聯級聯四個濾波器(如果相移為每個 RC 振蕩器 45 度)并獲得 180 度。

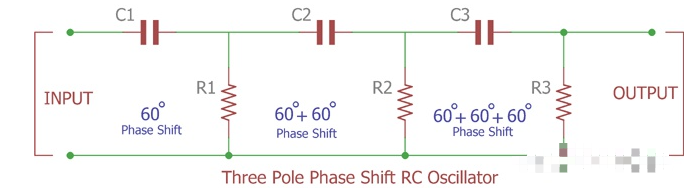
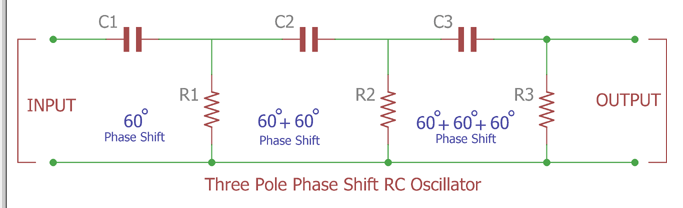
在此圖像中， 三個 RC 振蕩器級聯，每次添加 60 度相移 ，最后在第三級之后我們將獲得 180 度相移。

我們將在仿真軟件中構建此電路，并查看電路的輸入和輸出波形。讓我們先看看電路的圖像，同時也會看到示波器連接。

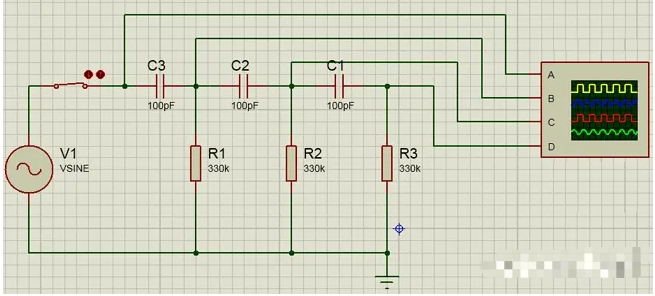
在上圖中，我們使用了 100pF 電容和 330k 電阻值。示波器連接在輸入 VSIN(A/黃色通道)、第一個極點輸出(B/藍色通道)、第二個極點 輸出

(C/紅色通道)和第三個極點(D/綠色通道)的最終輸出之間。

級聯四個 RC 濾波器：

在下圖中，四個 RC 相移振蕩器分別使用 45 度相移，在 RC 網絡末端產生 180 度相移 。

使用晶體管的 RC 相移振蕩器：

這都是 RC 振蕩器中的無源元件或組件。我們得到 180 度的相移。如果我們想要進行 360 度相移，則需要一個有源組件 來產生額外的 180 度相移。這是由晶體管或放大器完成的，需要額外的電源電壓。下面的電路顯示了使用 BJT 的 RC 移相振蕩器。

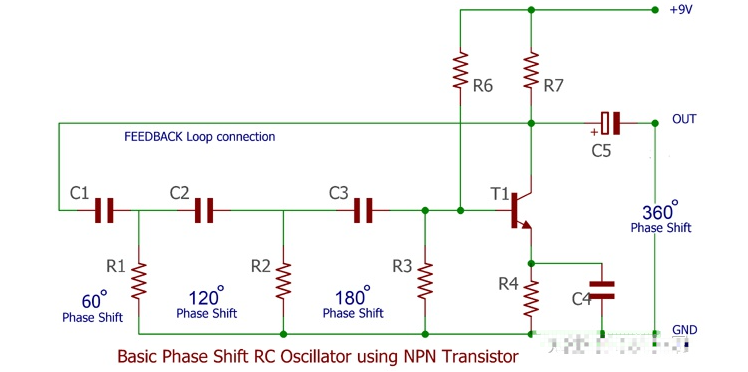
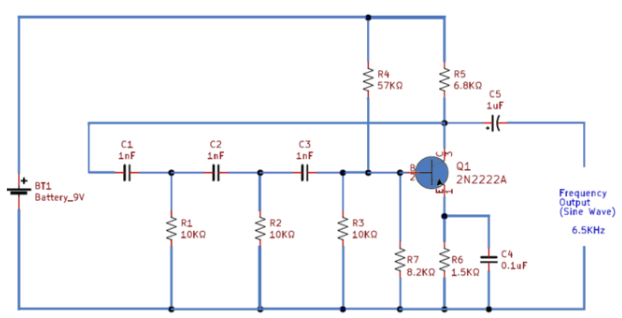
在此圖中， NPN 晶體管用于產生 180 度的相移 ，而 C1R1 C2R2 C3R3 將產生 60 度的相位延遲。因此，累積這 三個 60 + 60 + 60 = 180 度相移，另一方面通過晶體管添加另一個 180 度，創建總 360 度相移。 我們將在 C5 電解電容器上獲得 360 度相移 。如果我們想改變這種改變電容器值的方法的頻率，或者通過消除單獨的固定電容器在這三個極上單獨使用可變預設電容器。

建立反饋 連接 以使用該三極 RC 網絡將能量檢索回放大器。這是穩定的正振蕩和產生正弦電壓所必需的。由于反饋連接或配置， RC 振蕩器是反饋型振蕩器 。

1921 年，德國物理學家海因里希·格奧爾格·巴克豪森 (Heinrich Georg Barkhausen) 引入了“巴克豪森準則”，用于確定反饋回路中相移之間的關系。根據標準，只有當反饋回路周圍的相移等于或 360 度的倍數并且回路增益等于 1 時，電路才會振蕩。如果相移在所需頻率上是準確的并且反饋回路產生 360 度振蕩，則輸出將是正弦波。RC 濾波器用于實現此目的。

RC相移振蕩器的頻率：

我們可以輕松確定相移振蕩器電路的頻率：

其中：

R = 電阻(歐姆)

C = 電容

N = 使用/將使用的 RC 網絡數量

此公式用于高通濾波器相關設計，我們也可以使用 低通濾波器并且相移將為負。在這種情況下，上面的公式將無法用于計算振蕩器的頻率，將適用不同的公式。

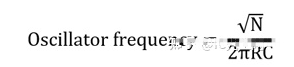
其中：

R = 電阻(歐姆)

C = 電容

N = 使用/將使用的 RC 網絡數量

使用運算放大器的RC相移振蕩器：

由于可以使用晶體管即 BJT 構建 RC 相移振蕩器，因此使用 BJT 的 RC 相移振蕩器還有 其他限制。

它對低頻穩定。

僅使用一個 BJT 輸出波的幅度并不完美，需要額外的電路來穩定波形的幅度。

頻率精度并不完美，也無法避免噪聲干擾。

不利的加載效果。由于級聯形成，第二個極點的輸入阻抗改變了第一個極點濾波器的電阻器電阻特性。級聯的濾波器越多，情況就越糟，因為它會影響計算相移振蕩器頻率的準確性。

由于電阻器和電容器兩端的衰減，每級的損耗都會增加，總損耗約為 輸入信號總損耗的1/29 。

由于電路衰減為 1/29，需要恢復損失。

現在是用運算放大器更換 BJT 的時候了 。如果我們使用運算放大器代替 BJT，我們還可以彌補這四個缺點并獲得更多的控制余量。由于高輸入阻抗，負載效應也得到了有效控制，因為運算放大器輸入阻抗促進了整體負載效應。

現在，無需進一步修改， 讓我們用運算放大器更改 BJT ，看看使用運算放大器的 RC 振蕩器的電路或原理圖是什么。

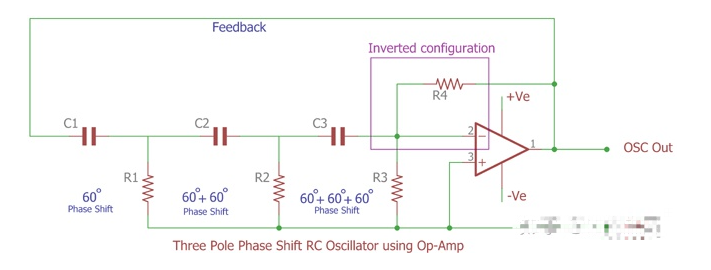
正如我們所見，BJT 被一個反相運算放大器所取代。反饋環路連接在第一個極點 RC 振蕩器上，并饋送到運算放大器的反相輸入引腳。由于這種反向反饋連接， 運算放大器將產生 180 度相移 。三個 RC 級將提供額外的 180 度相移。我們將在名為 OSC out 的 運算放大器第一個引腳上獲得所需的 360 度相移波輸出。 R4 用于運算放大器的增益補償。我們可以調整電路以獲得高頻振蕩輸出，但這取決于運算放大器的頻率范圍帶寬。

此外，為了獲得所需的結果，我們需要計算增益電阻 R4 以 在運算放大器上實現29倍的更大幅度，因為我們需要補償 RC 級的1/29損失。

讓我們看看，我們將制作一個具有真實元件值的電路，看看 RC 相移振蕩器的模擬輸出是什么。

我們將使用 10k 歐姆電阻和 500pF 電容器并確定振蕩頻率。我們還將計算增益電阻的值。

N= 3，因為將使用 3 個階段。

R = 10000，因為 10k 歐姆轉換為歐姆

C = 500 x 10 -12因為電容器值為 500pF

輸出為 12995Hz 或相對接近的值為 13 KHz。

由于需要 29次運算放大器增益， 因此使用以下公式計算增益電阻的值：

增益 = R f / R 29 = Rf / 10k 射頻= 290k

這就是 使用 RC 組件和運算放大器構建相移振蕩器的方式。您可以 通過以下鏈接了解有關使用運算放大器的 RC 相移振蕩器的更多信息。

RC 相移振蕩器的應用 包括放大器，其中使用音頻變壓器和需要差分音頻信號但反相信號不可用，或者如果任何應用需要 AC 信號源，則使用 RC 濾波器。此外，信號發生器或函數發生器使用 RC 移相振蕩器。

審核編輯：湯梓紅