有時為了某些測試需求，需要仿真產生一些數據。 這時，我們可以通過調取指令或自行編寫程序來生成這些隨機數據。

以下以博途為例，簡要說明了隨機數產生的幾種方式：

一、讀取系統時間的納秒作為隨機數

以固定周期直接將系統時間中的納秒輸出到對應變量。

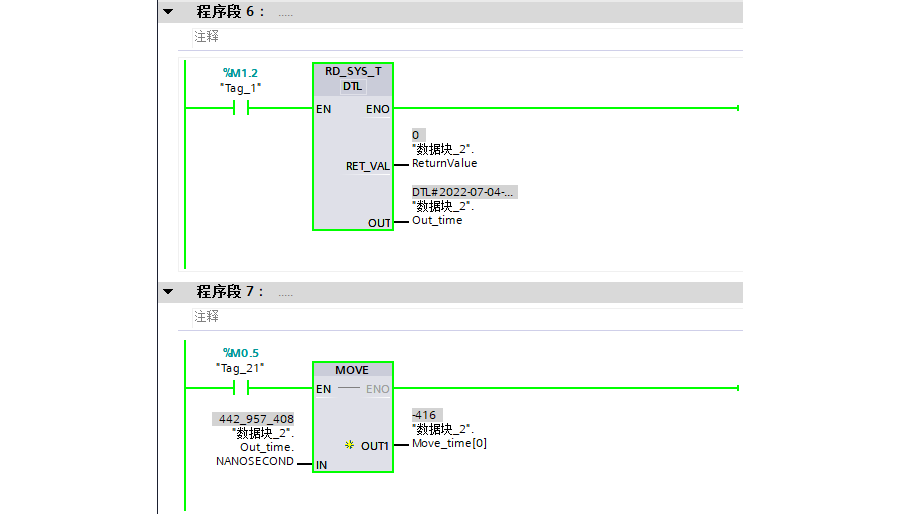
系統時間中的納秒為UDINT類型，轉為INT后，丟棄了高字部分

監視實時的系統時間，取其中的納秒(NANOSECOND，1秒=10^9納秒)

監視一下生成的隨機數的范圍：-32258—32751（5分鐘）

后續可繼續對此數據處理，縮放到需要的區間。

二、由LGF庫(官方提供的通用函數庫)內的隨機數程序生成

該指令原理也是采用納秒，不過處理過程更加細化、完善。

LGF庫

隨機數生成程序如下(只貼了其中關鍵的計算過程)：

REGION Calculating random number
    // 將納秒轉換為雙字以便尋址單個字節
    #tempNanoSecondInDWord := UDINT_TO_DWORD(#tempTime.NANOSECOND);
    // 以片段訪問方式將納秒進行字節交換
    #tempRandomValue.%B3 := #tempNanoSecondInDWord.%B0;
    #tempRandomValue.%B2 := #tempNanoSecondInDWord.%B1;
    #tempRandomValue.%B1 := #tempNanoSecondInDWord.%B2;
    #tempRandomValue.%B0 := #tempNanoSecondInDWord.%B3;
    // 隨機數標準化
    #tempNormReal := UDINT_TO_REAL(DWORD_TO_UDINT(#tempRandomValue)) / UDINT_TO_REAL(#MAX_UDINT);
    // 隨機數縮放
    #LGF_RandomRange_Real := ((#tempNormReal * (#maxValue - #minValue) + (#minValue)));
    #error := false;
    #status := #STATUS_FINISHED_NO_ERROR;
    #subfunctionStatus := #SUB_STATUS_NO_ERROR;
    // ENO mechanism is not used
    ENO := TRUE;
END_REGION

在主程序中調用，可設置上下限

三、線性同余法(LCG，Linear Congruential Method)

該方法的核心是以下遞歸公式：

RandNum =(A * RandNum + B)% M

A、B、M均為常數，其中A是 乘數 ，B是 增量 ，M是 模數 ，RandNum是 初始值 ，A、C、M的取值是保證產生高質量隨機數的關鍵。

可以看出，每次新產生的隨機數都跟上一次的數有關系。 隨機數序列中的初始值，我們通常叫做種子。 隨機數的產生需要設置種子，否則隨機數的結果每次運行都將一樣。 通常，我們使用系統時間的納秒作為種子(某些將此作為缺省設置)，這在一定程度上保證了種子的唯一性。

由于計算過程最后是對M取余數，余數的范圍就是0—(M-1)，這決定了產生的隨機數是有周期性的。 M的大小決定了最大周期的長短，一般取值域的最大值，而A和B也會影響周期。 A、B、M的選取多種多樣，只要保證產生的隨機數有較好的均勻性和隨機性即可。

FC塊，變量定義為雙整型。 模數M可以取值域最大值2^32

種子seed可以采用系統時間或自行設置

隨機數曲線

線性同余法的初始值一旦確定，輸出的序列將固定。 而當獲取某些隨機數序列后，其初始值以及A、B、M也會被反向計算出來。

對于其缺點，可以考慮以下改進方式，每產生n個數，將當前時鐘值MOD M得到的余數作為新的種子。

四、平方取中法

平方取中法由馮·諾依曼提出，它的原理是：首先取一個2s位的整數(種子)，平方，得4s位整數，然后取此4s位中間的2s位作為下次運算的種子。 重復該過程，即可得到一個隨機數序列。 (序列中每個數縮放至0.0—1.0范圍內)

例如：取種子365，平方得133225，高位補0，取中間1332，平方得1774224，高位補0，取7742，以此類推.........

#RandInt := SQR(#Seed);
#Seed := (#RandInt MOD 1000000 - #RandInt MOD 100) / 100;
#RandReal := DINT_TO_REAL(#Seed) / 9999.0;

隨機數測試結果

在實踐中，這種方法其實并不好用。 很難說明取什么種子才能保證足夠長的周期。 以種子123為例，在40多個周期后，種子末位便退化產生了00，之后的隨機數成了固定的幾個數值，周期極短。 該算法也有改進空間。

梅森旋轉算法_Mersenne Twister

梅森旋轉算法可以產生高質量的偽隨機數，且效率高效，彌補了以上偽隨機數生成器的不足和缺陷。 它在C++、Python等編程語言中均有應用。

理解該算法前需要先了解許多前置名詞，線性反饋移位寄存器、級、反饋函數、抽頭序列、本原多項式...... 實在有興趣的可以搜索一下。 我，放棄了。

說到隨機數，不禁想到了因果律：果由因生、有依空立 、事待理成。

所謂的“隨機”，大概不過是事物發展中的個體因為信息偏差，產生的局限認知。