觀察點
為了仿真變換器加上補償網(wǎng)絡(luò)后的傳遞函數(shù),可以直接把環(huán)路在誤差電壓處斷開,以占空比信號為輸入,誤差電壓為輸出,進行交流分析。 所謂的斷開,其實可以與之前一樣,接入一個大電感和大電容即可。

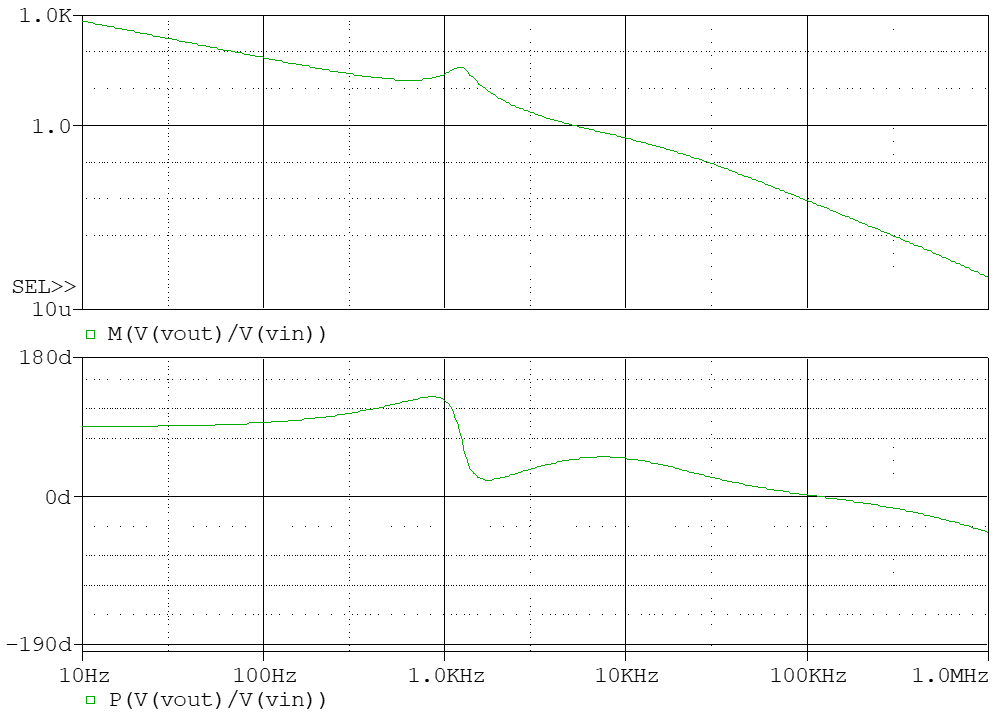
注意這里忽略了放大器引入的相移,因此相位從正的開始,相位裕度以與0°線的距離計算。 可見補償后的系統(tǒng)相位裕度抬高了。
頻域參數(shù)
當輸出信號和控制信號之間的相位差減少為0°,則變成正反饋振蕩器。
交叉頻率處的輸出容抗可以近似表示閉環(huán)輸出阻抗,所以可以近似計算出輸出瞬態(tài)階躍電流作用下的輸出電壓脈沖
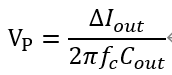
根據(jù)這個式子以及穩(wěn)態(tài)紋波需求,可以確定交叉頻率的取值。 不過對于有RHPZ的拓撲,一般就直接選定為RHPZ所在頻點的30%,同時又應(yīng)該保證交叉頻率在LC諧振頻率的5倍以上,給設(shè)計帶來困擾。 對于沒有RHPZ的拓撲,可以直接設(shè)定為開關(guān)頻率的20%以下。 脈沖峰值固然與上式有關(guān),不過恢復時間則由相位裕度決定。
構(gòu)建補償網(wǎng)絡(luò)
構(gòu)造零極點的知識均已知曉。 值得一提的有構(gòu)造RHPZ的方法,就是將原輸入信號與高通濾波器后的信號相減
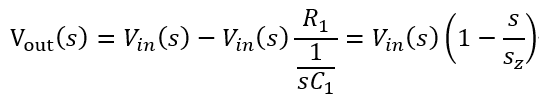
零點頻率即RC分之一。
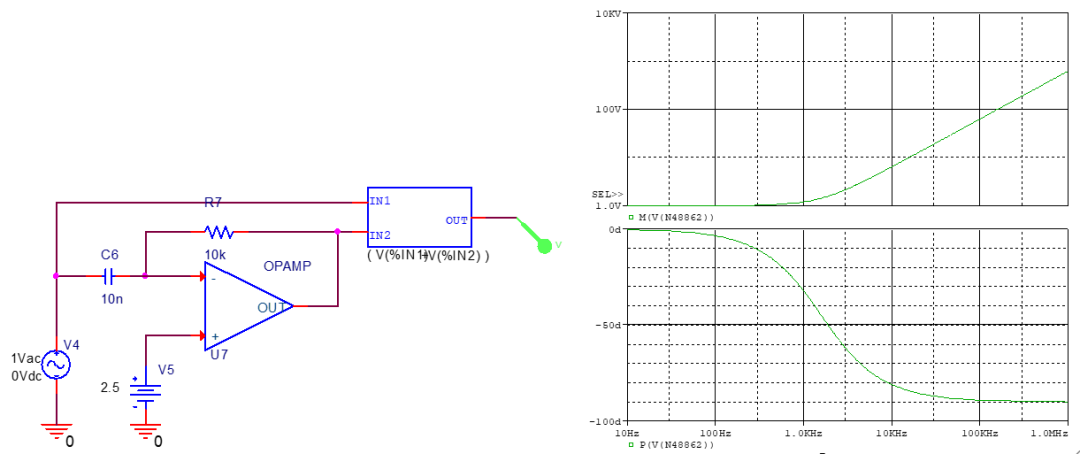
RHPZ是變換器間接能量傳輸?shù)慕Y(jié)果。 在CCM的Boost變換器中表現(xiàn)為,如果負載出現(xiàn)向上的階躍,造成占空比信號變大,即減小,即電感向負載供電流的周期減小。 但是電感電流不會馬上增大,而是以固定步長增加,這個過程中輸出電流可能會反而比原來更小,這就是RHPZ的影響。 如果系統(tǒng)響應(yīng)很快,那么在負載躍變瞬間,反饋環(huán)的占空比輸出會因為輸出電壓的反向減小而迅速增大到1,使變換器無法工作,這也是Boost變換器環(huán)路設(shè)計要降低交越頻率的原因。 一般選擇在最低RHPZ的1/3處。 DCM時變換器仍存在RHPZ,但其被推到高頻處,因此環(huán)路設(shè)計的困難相應(yīng)降低。
各個頻率響應(yīng)對應(yīng)的有源電路網(wǎng)絡(luò)依次示下:
積分器
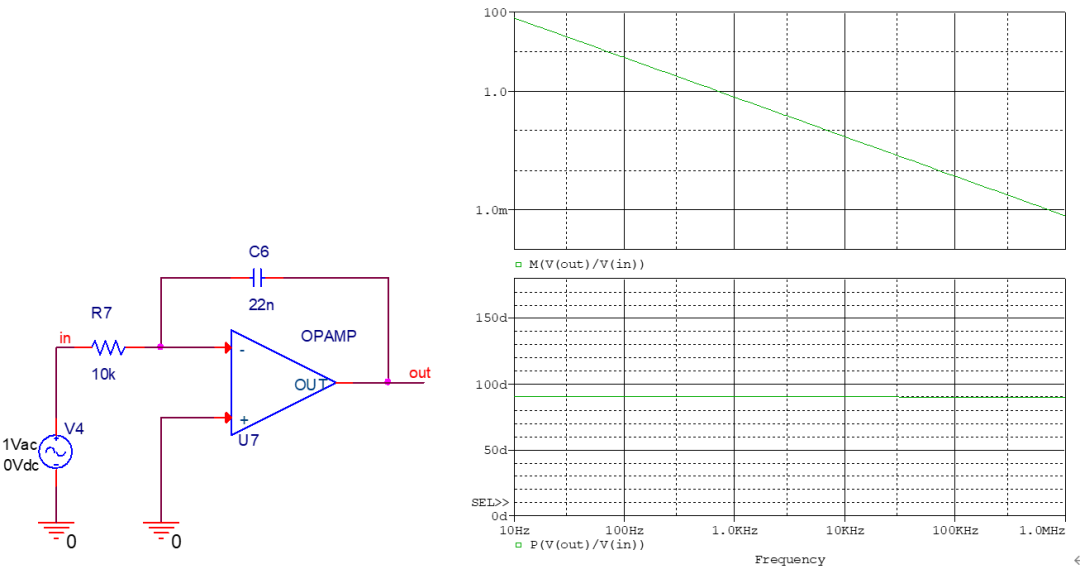
零極點
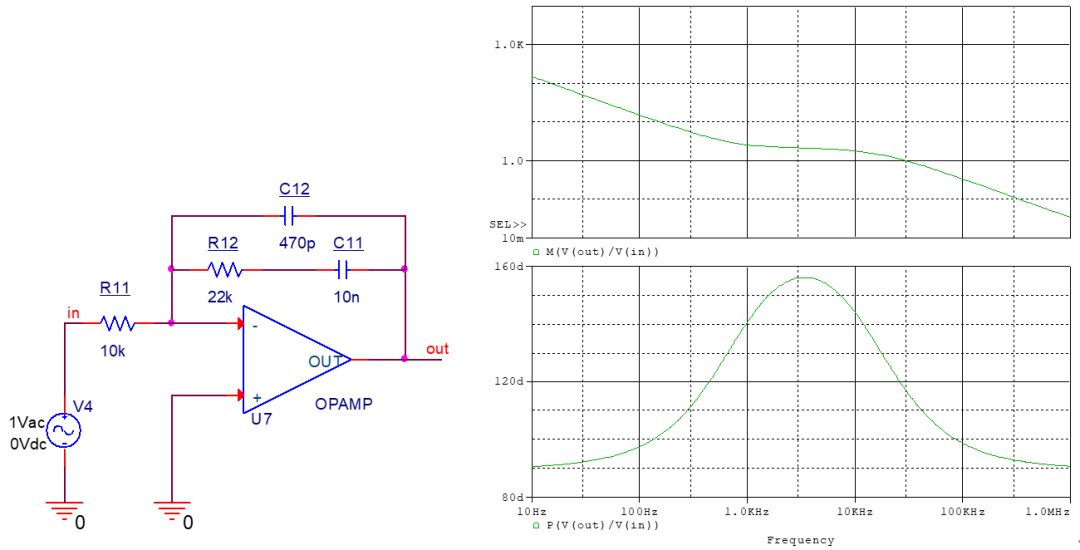
極點位置為
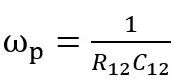
,零點位置為
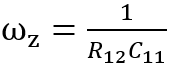
,并且有積分器的效果。 這種補償網(wǎng)絡(luò)的特點是中頻部分存在一個固定增益區(qū),并且該區(qū)域的相位具有超前性質(zhì),相位的最大值出現(xiàn)在頻率為
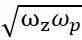
處。 用于電流模式和DCM。
零極點對a
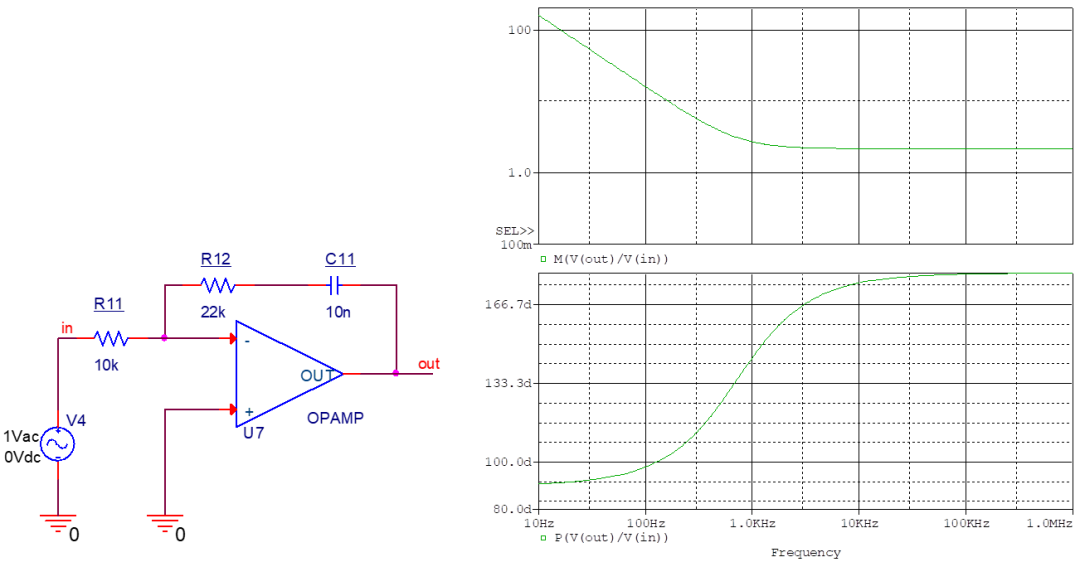
這是上面的特殊情況,即C12為0時,極點被排除,因此不存在高頻段的增益下降,相位也一直接近同相。 在無需考慮ESR零點的場合可以用這個簡化的補償器。
零極點對b
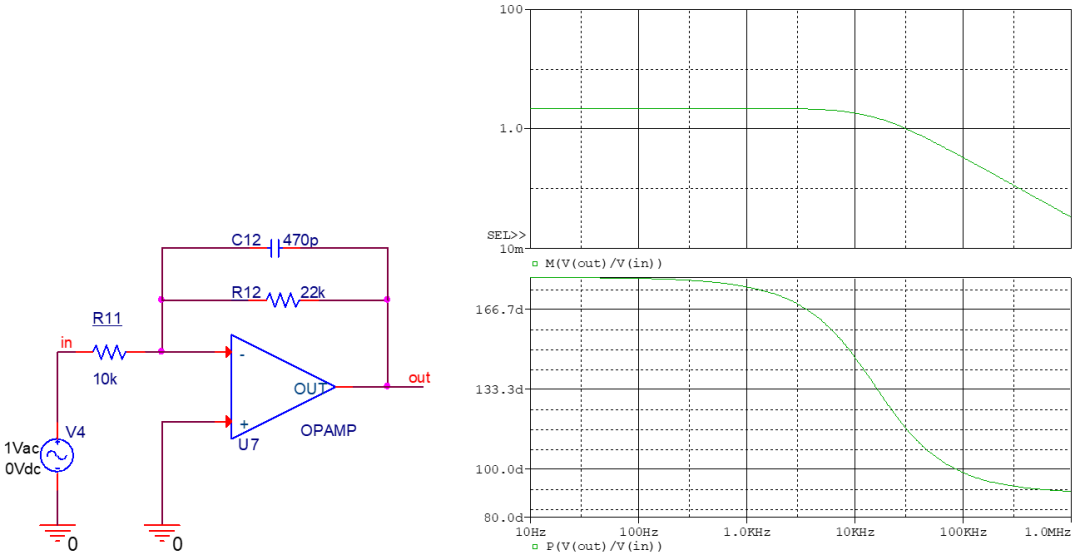
這也是上面的特殊情況,令C11為無窮大,則變成一個原點處的零點,相當于與積分器的效果相抵消,因此低頻至中頻都為固定增益。 明顯的缺點是直流增益太低,穩(wěn)態(tài)精度無法保證。
兩個零極點對
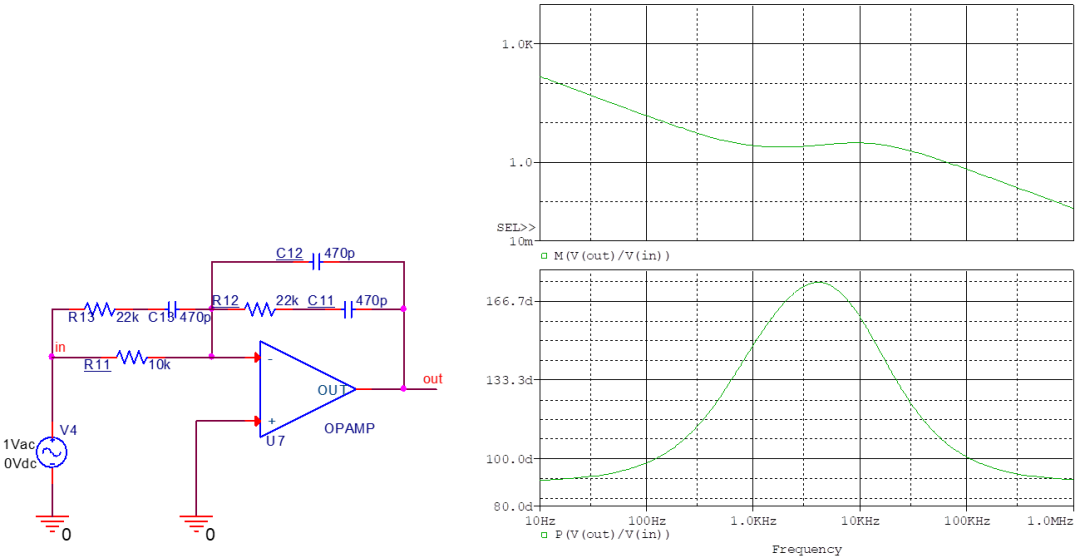
傳遞函數(shù)為
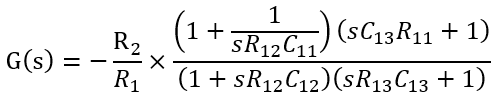
式中就可以看出零極點位置和直流增益。 比起單個的零極點對,兩個零極點對提供了更大的直流增益和更大的超前相角,因此是最完備的一種補償網(wǎng)絡(luò)。
注意,實際的運算放大器必定自身附帶一個低頻的極點,其本身的增益就隨頻率的增大而減小,所以實際設(shè)計時還需要根據(jù)具體的運放進行參數(shù)設(shè)計。
K因子
一種從變換器開環(huán)特性得到k因子等參數(shù)值后,直接推導各類型補償網(wǎng)絡(luò)組件參數(shù)的方法。
首先看各類型補償網(wǎng)絡(luò)需要考慮的補償參數(shù)。
積分器:極點在原點處,所以它只能通過平移增益曲線,改變系統(tǒng)的交叉頻率,并引入一個90°的相移。
零極點對:除了具有積分器的平移曲線的效果外,還引入了一個超前相位,某點引入的相位增加量計算為
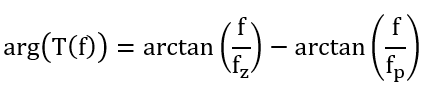
因此在交叉頻率處,用k因子的方法可以令極點頻率為kf,零點頻率為k分之一f,則相位增加量

解出
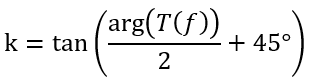
根據(jù)所需要的相位裕度和變換器本身的相移,加上積分器引入的90°相移來確定
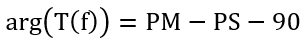
書中給出了不同k值下該補償器的響應(yīng),k=1時退化為積分器,隨著k增大,零極點距離增大,超前的相位增大,而直流增益減小。
雙零極點對:與上面相似,這里假設(shè)雙零點重疊,雙極點也重疊,那么令極點頻率為倍的f,則
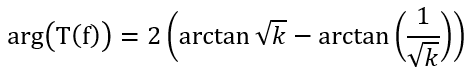
解出
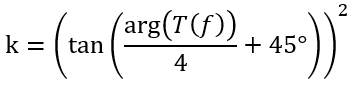
接下來的式子和關(guān)系與上述一致。
K因子設(shè)計步驟
1、獲得變換器交流響應(yīng)。
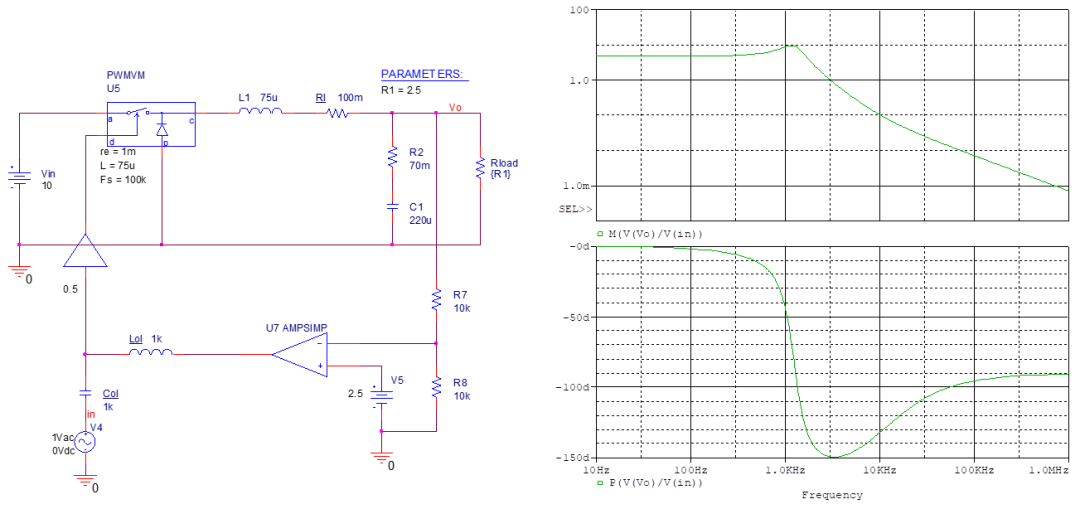
用游標看出交叉頻率為3kHz,相移149°。
2、選擇交叉頻率和裕度。
開關(guān)頻率為100kHz,而LC峰值頻率為
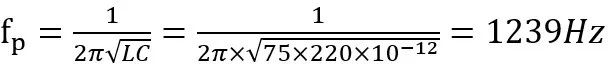
如前所述應(yīng)該選取6k以上的交叉頻率,但是書中選取了5k,先按書中選取,后面再觀察不同。
若選取5k,先觀察變換器響應(yīng)中5k處的數(shù)據(jù),得到相移為-146°,增益為-9.2dB,期望的相位裕度為45°。
3、選擇補償器類型。
可見到變換器的響應(yīng)相位滯后達到180°,穩(wěn)妥起見可以選擇雙零極點對補償器,最高可以補償180°超前相位。
4、應(yīng)用公式計算組件。
運用上頁的公式,計算出k因子和元件參數(shù)
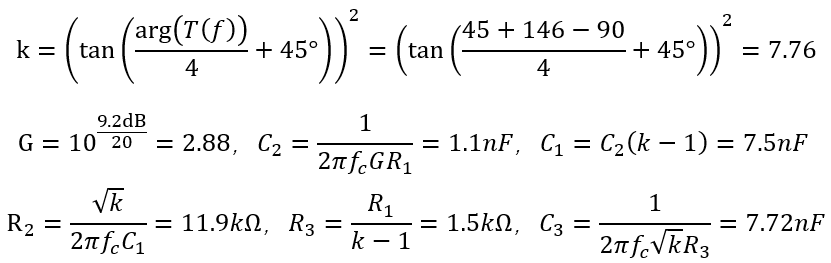
順便可以計算出補償器提供的零點和極點頻率分別為1.8k和14k。
5、連接補償器后開環(huán)掃描。
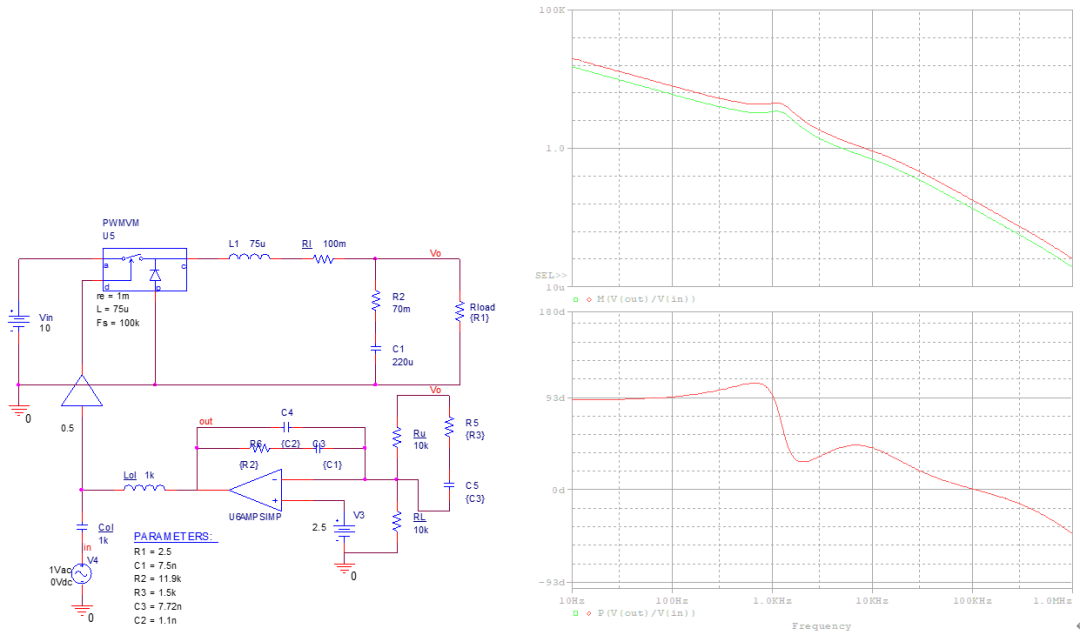
標準輸入并帶滿載情況下的開環(huán)響應(yīng),交叉頻率為5kHz,相位裕度為43°。 變化輸入電壓為20V,即圖中紅線所示,環(huán)路增益增加了1倍,即曲線被抬高了3dB,因此交叉頻率變?yōu)?.45kHz,相位裕度為44°。
6、變化ESR和負載檢查相位裕度。
以上測得是負載電阻為2.5Ω即電流為2A時的響應(yīng),若增大電阻至進入DCM模式,觀察補償器的功能是否受影響。 下圖看出,因為變換器在低頻處退化為一階系統(tǒng),低頻段增益減小,所以交叉頻率明顯降低,分別為613Hz和1kHz,相位裕度分別為39.5°和59.5°,在不同輸入電壓下的相位裕度相差更大了,即對輸入電壓更加敏感。
如果變化電容的ESR,道理相同,負載恢復滿載情況,若取值變?yōu)?00m時如下圖,交叉頻率變?yōu)?.83kHz和15.56kHz,相位裕度變?yōu)?4°和55°。 可見ESR的增大會使得其零點提前出現(xiàn),使得交叉頻率后移,并且提高中頻段的相位。
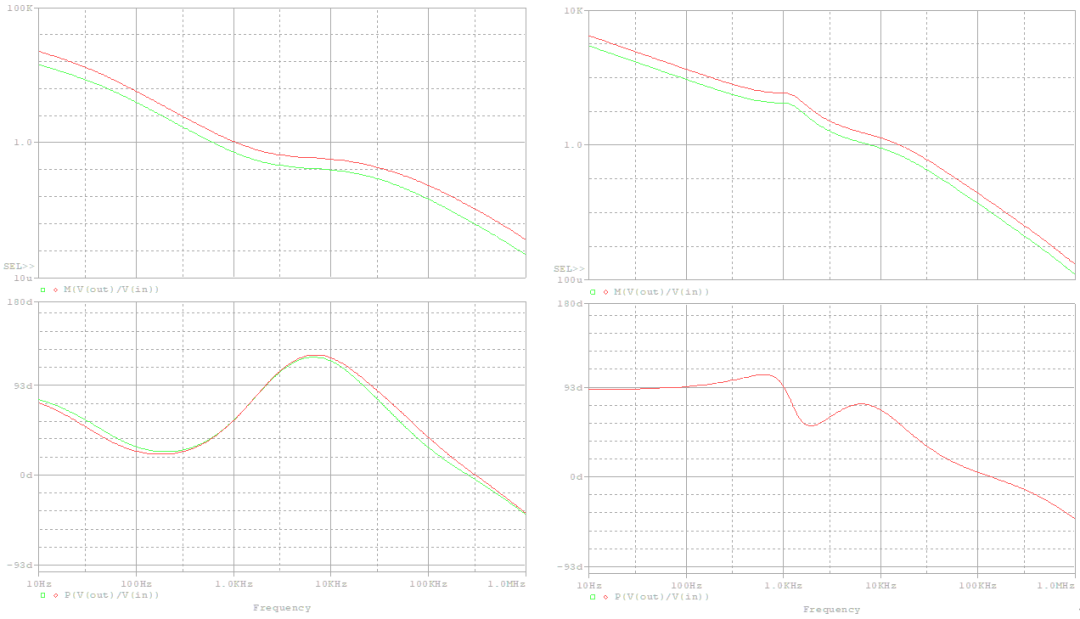
負載為50Ω時 ESR為200m時
7、觀察瞬態(tài)響應(yīng)。
前面給出了一個近似估計電流上升階躍下,電壓響應(yīng)尖峰的計算式
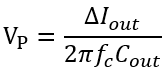
如果作0.1A到2A的階躍,大致算出峰值為
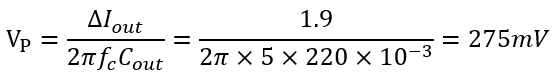
即從5V下降到4.725V。 搭建仿真模型,用ABM+脈沖信號源實現(xiàn)負載切換,結(jié)果如下
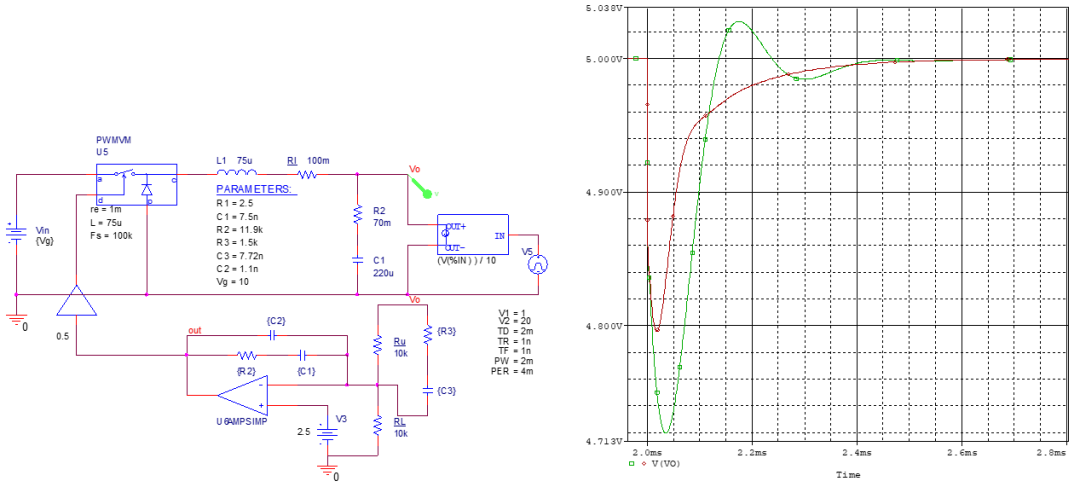
電壓跌落為4.713V,與計算值近似相等,誤差可能來自ESR等。 書中給出該式,只說明用來計算欠脈沖,若用來計算電流下降階躍下的電壓超調(diào),則似乎不符合仿真結(jié)果的5.24V。
下圖給出了全貌,明顯,DCM下到CCM的切換很快,建立時間大約0.4ms,而DCM切換到CCM則很慢,需要大約5ms。
圖中同樣以紅線示出了20V輸入電壓下的瞬態(tài)響應(yīng),說明Buck變換器中確實是以最低輸入電壓為最惡劣條件,而高輸入電壓下具有更好的動態(tài)性能。
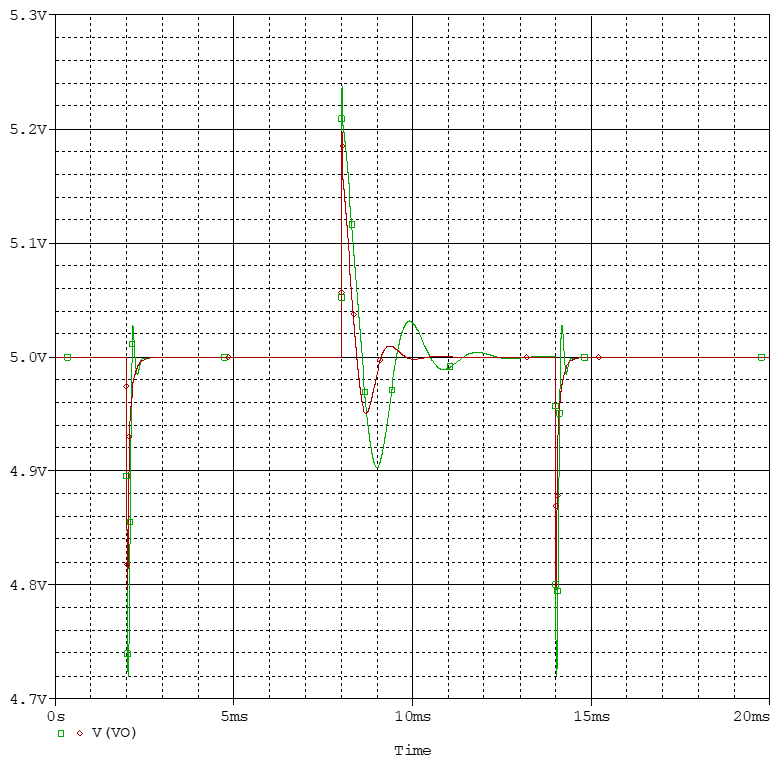
除了輸出電壓響應(yīng)外,還應(yīng)觀察誤差電壓的瞬態(tài)響應(yīng),這才是變換器在控制意義上的輸出。
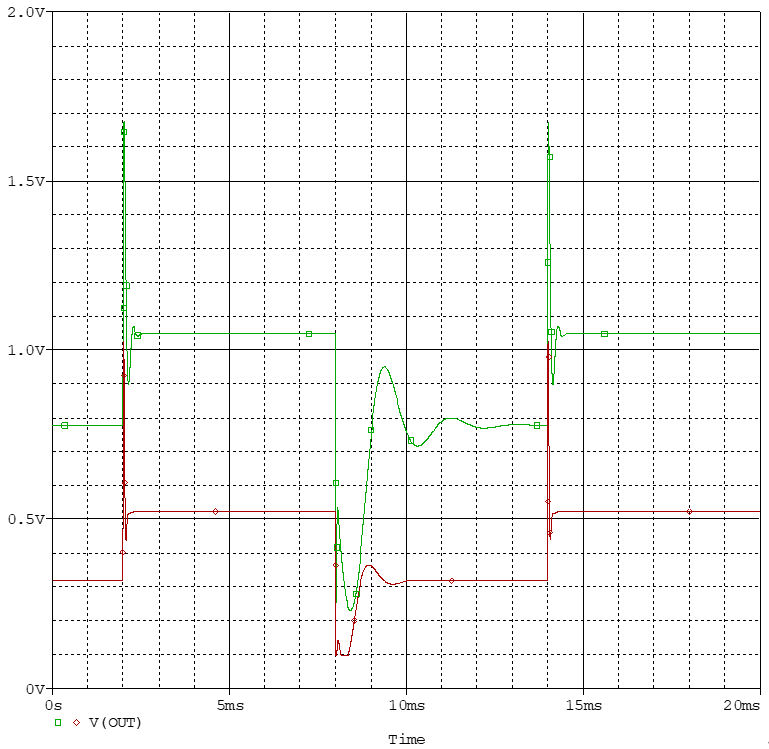
書中到后面也說明了當交叉頻率為8kHz時,響應(yīng)峰值降低為171mV,系統(tǒng)性能應(yīng)是有所改善。 重復上述步驟,8k處的曲線數(shù)據(jù)為相移137°,增益-16.5dB,同樣選擇45°裕度,雙零極點對補償器,列式如下。
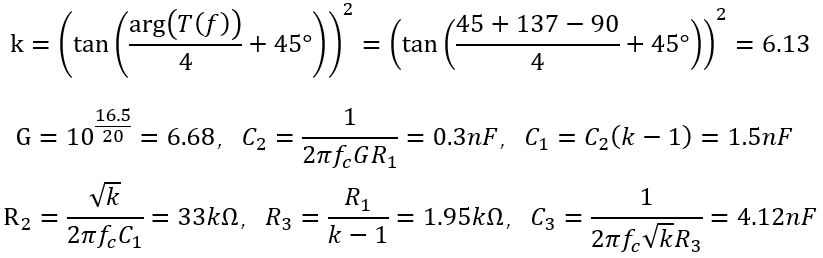
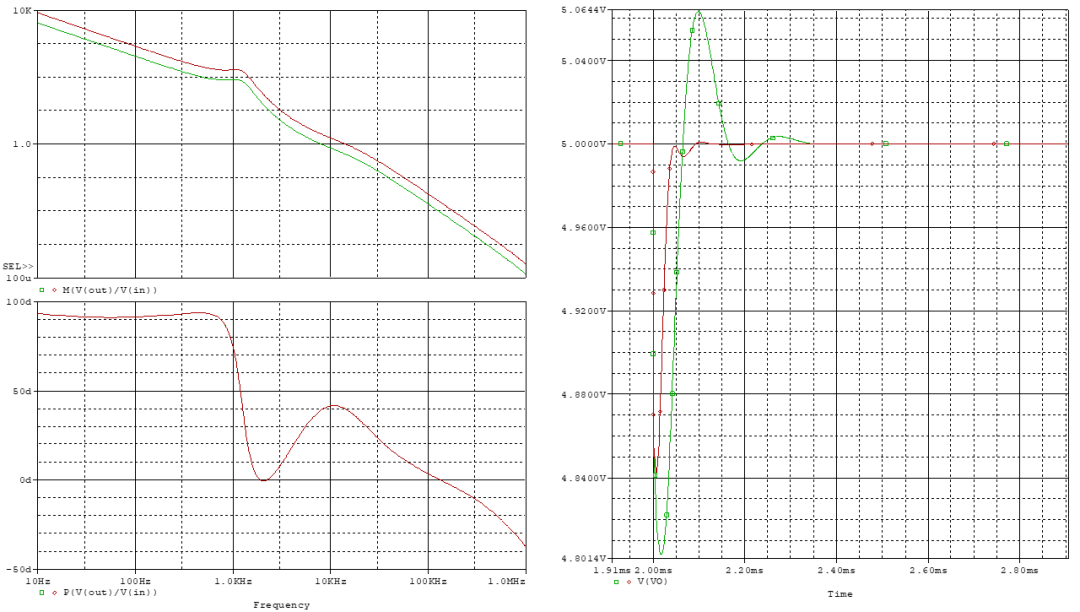
得到曲線如上,與前述相同,用輸入電壓分別為10V和20V時進行對比,10V時,交叉頻率為7.98kHz,相位裕度為42°。 再觀察瞬態(tài)響應(yīng),理論計算的峰值應(yīng)為,圖中為4.8V左右,相差不大,說明該估計式具有足夠的精確度。 仔細觀察上圖中的相位曲線,可以看出一些問題。
K因子法的缺陷
該方法雖然簡單,它對響應(yīng)曲線形狀忽略不計,即忽略了可能存在的諧振峰,而只考慮交叉頻率。 這樣有可能在交叉頻率之前出現(xiàn)相位裕度減小到0的情況,如上圖所示。 在交叉頻率較高為8k時,出現(xiàn)了相位降低到0,增益仍為10以上的情況,這樣在該頻點很容易就有振蕩現(xiàn)象,稱為條件穩(wěn)定。 這種問題出現(xiàn)的原因是K因子法在放置零極點時只考慮交叉頻率的實現(xiàn),而并未考慮零點位置與LC極點位置大致重疊這一要求,所以就會出現(xiàn)無法抵消LC極點引起相移的問題。 所以K因子法好雖好,若要妥善設(shè)計,還是應(yīng)該采取一般的零極點放置法進行配置。
這種一般的方法,精確放置了每一個零極點,可以制作專用的計算表格。 書中提供了一種利用仿真軟件進行參數(shù)計算的圖紙,似乎只能用Ispice,Pspice尚不知可否。
用放置零極點的方法,就不會出現(xiàn)條件穩(wěn)定性的問題了,圖如下,相位裕度為36°。 這種方法的缺陷也正是K因子法的優(yōu)點,即交叉頻率無法精確定位; 另外,書中的理論和實驗也表明,K因子法放置的零點頻率較高,瞬態(tài)響應(yīng)也會快于放置零極點的方法。 所以各存利弊。
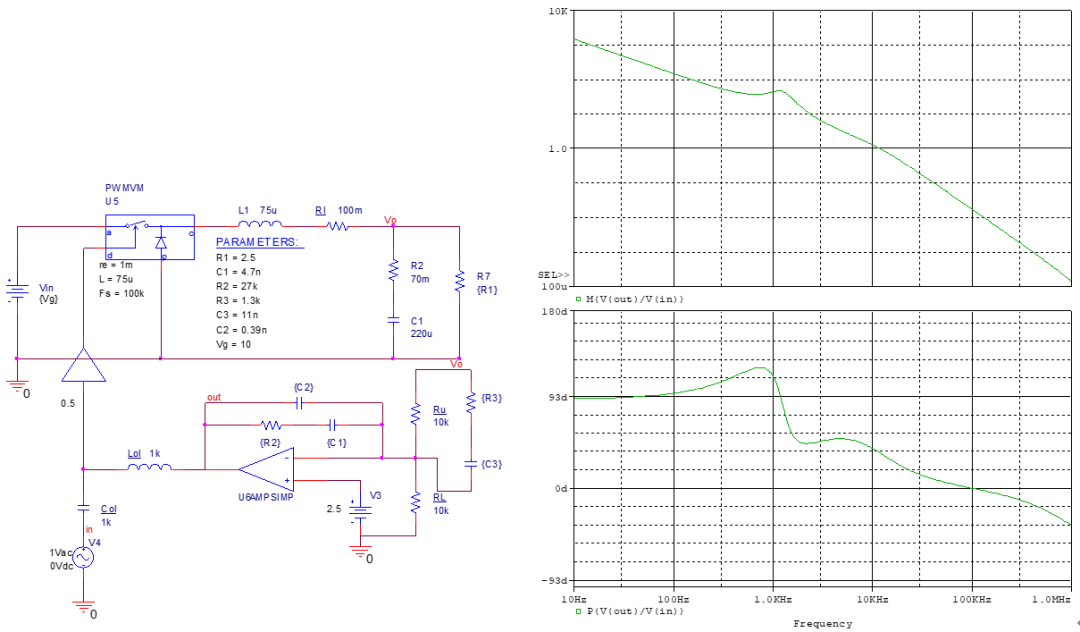
電流模式補償網(wǎng)絡(luò)
以上討論的內(nèi)容均針對二階的電壓模式Buck電路。 對于電流模式控制來說,變換器的模型在低頻呈現(xiàn)為一階系統(tǒng)。
回顧一下電流模式控制的相關(guān)設(shè)置。 為避免次諧波振蕩,需要加入斜坡補償,在輸入電壓為10V時,電路中電感電流的上升和下降斜率一樣都為66mA/μs,補償斜率可以為其一半。 若采集電阻阻值為0.4Ω,則補償斜坡電壓為13.3kV/s。
同樣運用K因子法,選擇交叉頻率為10kHz,相位裕度為80°。 先觀察開環(huán)曲線。
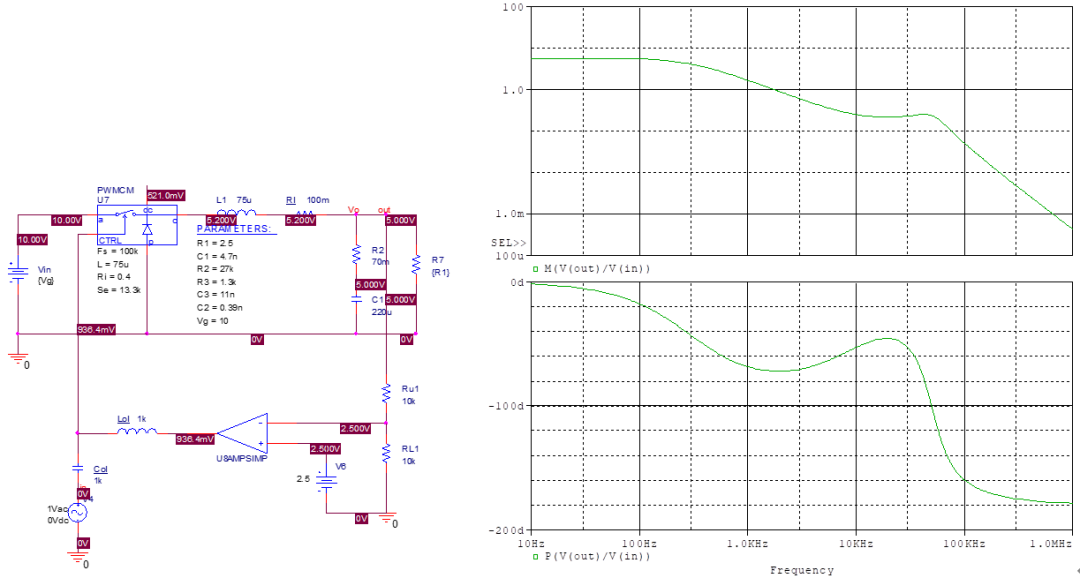
得到10kHz處相位為-52°,增益為0.25=>-12dB。 因為相位滯后在90°以內(nèi),可以用零極點對的補償器(2型)。
計算式如下
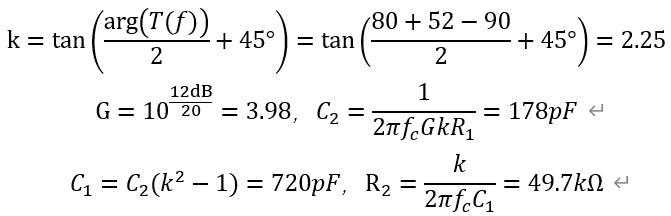
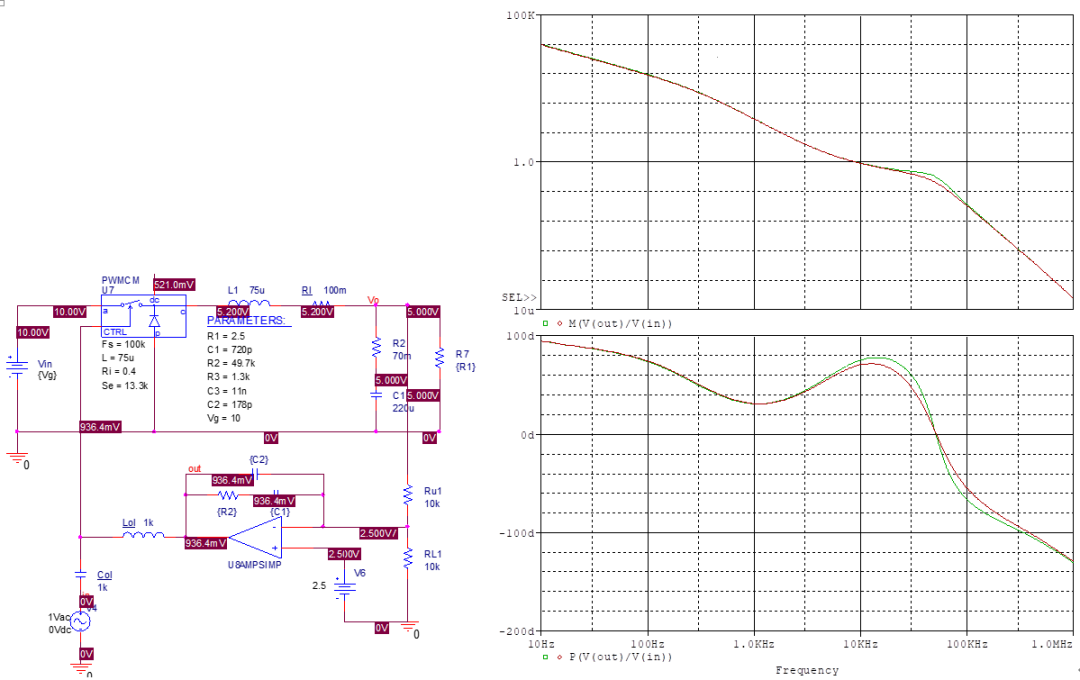
得到補償后的特性曲線如圖。 交叉頻率為9.1kHz,相位裕度74°。 值得注意的是在輸入電壓分別為10V和20V時,兩條曲線幾乎重合,這是因為電流模式控制下,理論上的音頻敏感度就是0,即輸入電壓的變化不會對系統(tǒng)造成影響。 略去了負載階躍測試,因為可知道電流模式控制下系統(tǒng)在低頻變?yōu)橐浑A系統(tǒng),自然在階躍作用下是不會產(chǎn)生振蕩的,但峰值電壓由輸出電容決定,對電壓模式和電流模式都是一樣的。
此例可以看出K因子法對電流模式的設(shè)計還是很有優(yōu)勢的,因為一階系統(tǒng)的特點,系統(tǒng)本身的相移就不大,所以不會出現(xiàn)條件穩(wěn)定性的問題。
實際設(shè)計之TL431反饋
實際工業(yè)應(yīng)用中已經(jīng)很少用運算放大器設(shè)計補償電路,而是將其與基準源合二為一,利用TL431內(nèi)部的集成誤差放大器就可以設(shè)計出高性能的補償電路。 TL431的參考電壓為2.5V,TLV431為1.24V,且電流更小。
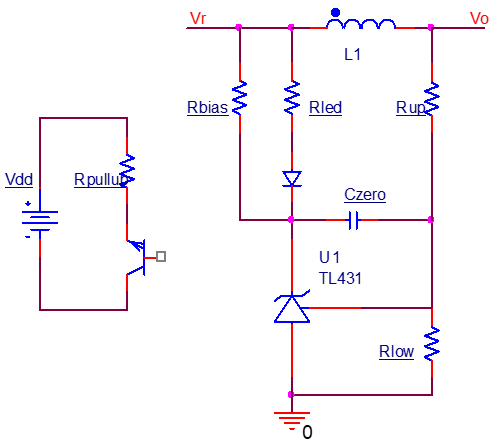
在一般的反饋環(huán)路中,連接光耦LED的支路為快支路,分壓網(wǎng)絡(luò)為慢支路,如圖所示。 對于小信號的研究,由于TL431的動態(tài)電阻與Rled比起來小得多,忽略后由KVL得
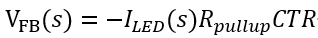
VFB為最終反饋回到芯片F(xiàn)B引腳的電壓。
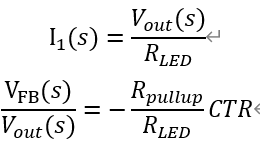
就得到了快通道的傳遞增益,在高頻區(qū)難以降低,使放置零點成為一個問題。
整個反饋可以看作快慢通道的疊加,與慢通道疊加后,推導反饋環(huán)路的傳遞函數(shù)
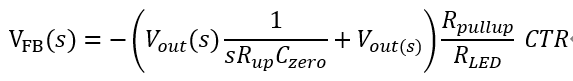
即
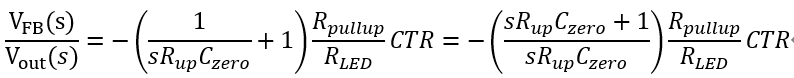
表明了系統(tǒng)中存在原點處極點和一個零點。
必須要明白的一點是,這個電路是實現(xiàn)前面所述補償網(wǎng)絡(luò)的方法。 對比零極點對補償網(wǎng)絡(luò),還缺少一個非原點處的極點,可以直接在光耦的輸出與地之間接入電容。 得到的零極點位置分別為
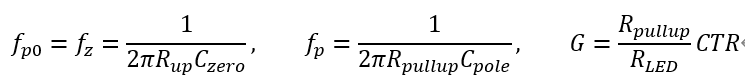
注意到第一條式子的關(guān)系,所以曲線的斜率剛好在0dB處發(fā)生轉(zhuǎn)折,結(jié)果就是中頻增益G與零極點位置無關(guān)。
下面用TL431實際設(shè)計補償器。
K因子+431
用k因子法直接把零極點放置在
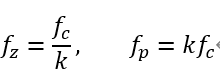
構(gòu)造零極點對的補償器做法較為簡單,基本上與前述的一般方法一致,直接代入計算即可,得到的響應(yīng)與前面用運放搭建的結(jié)果是一致的。
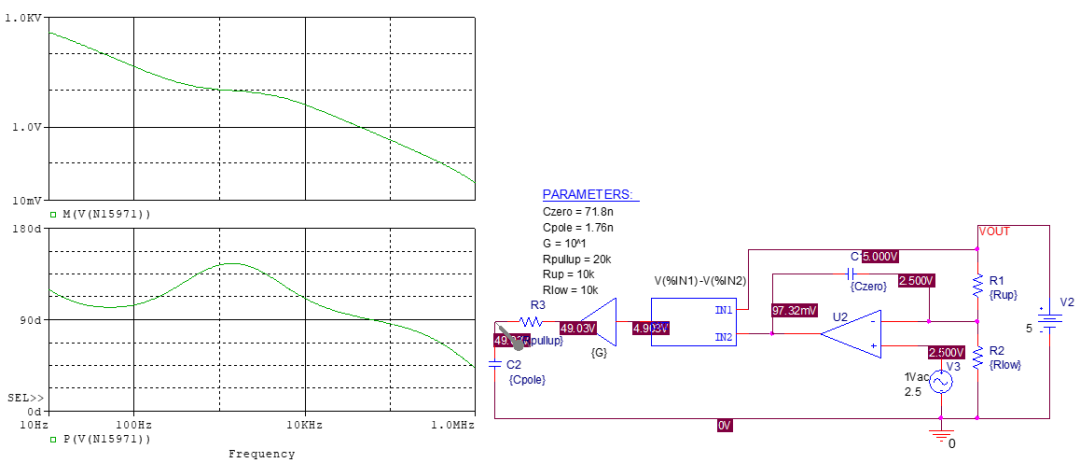
如果搭建雙零極點對補償器,則需要考慮快通道的影響,即高頻區(qū)存在的增益,它使得直接在上位反饋電阻并聯(lián)零點的做法沒有作用。 因此需要在快通道的LED電阻直接并聯(lián)RC網(wǎng)絡(luò),并聯(lián)后,原本LED電阻的位置上阻抗變?yōu)?/p>
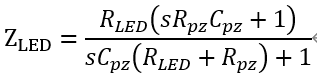
完整的傳函變成
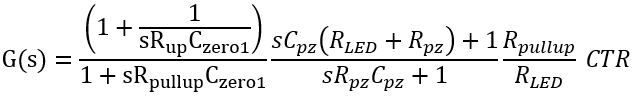
可得到兩對零極點的位置。 如果零點和極點的位置都重合,可以求出
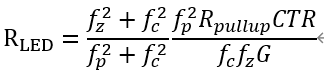
G為期望的交叉頻率處增益。 之后就可以根據(jù)零極點位置求出RPZ和CPZ的值。
一般不會用TL431搭建這種補償器,因為LED電阻對零極點位置存在影響,還是用運放搭建較好。
TL431偏置電流
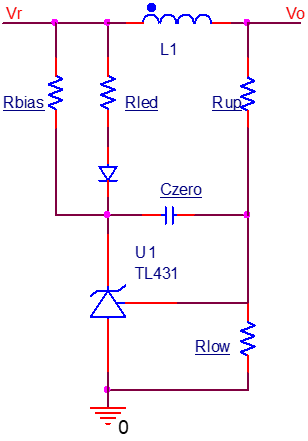
431需要一個從陰極流入的電流滿足要求,必須大于1mA,否則其開環(huán)增益會大大減小,使穩(wěn)壓效果變差。 一般不能依靠LED電阻提供的電流,因為光耦的CTR會使期望的電流衰減,最后不能達到1mA的要求,所以應(yīng)該另外增加偏置電阻,通過輸出電壓直接拉一個電阻到TL431陰極,或者在LED兩端并聯(lián)一個電阻都是可行的。
在僅僅靠LED電流提供偏置時,要考慮最大的光耦傳輸比。 先計算光耦輸出端需要的電流值為
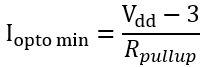
其中Vdd為控制器的邏輯電平,3V是假定反饋引腳的電壓上限值。 則LED的電流最小可能是
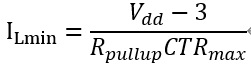
假設(shè)Vdd=5V,上拉電阻10k,CTR最大為100%,此時電流200μA,不滿足要求。 所以要加入偏置,由最小電流要求得到偏置電阻的取值
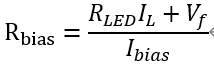
其中Vf為LED的壓降,典型值為1V。 若要求偏置電流2mA,LED電阻2.2k,Vdd=4.8V,CTR取典型值為30%,得到偏置電阻為830Ω。
此外還有一個地方的偏置電流需要注意,即從電阻分壓過來的電流,進入TL431的參考節(jié)點。 進入該節(jié)點的電流數(shù)據(jù)表給出為2~4μA,據(jù)此可以計算低端電阻值
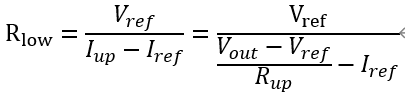
不過如果選擇高端電阻的電流遠大于μA級別,比如為1mA,就可以忽略這個電流值了。 對于低功耗應(yīng)用來說,還是應(yīng)當設(shè)定為更低的電流值,這時需要考慮這個電流的限制。
關(guān)于光耦
光耦的輸出端中,集電極和基極之間存在較大的電容,會影響可用帶寬,此帶寬由電容和上拉電阻共同決定。 從數(shù)據(jù)表中給出的下降時間和測試電阻值可以計算出結(jié)電容值
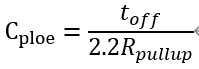
一般為nF級別。 因此對要求較大帶寬的電源,光耦會造成較大的影響,或者使用阻值很小的上拉電阻。
另外,光耦還存在著一個高頻的極點。
跨導放大器
輸出電流為兩個輸入電壓差的倍數(shù)。 特別之處在于跨導放大器不存在局部反饋,相當于開環(huán)運行,輸入端也沒有虛地的情況,而且分壓電阻的下位電阻在環(huán)路中起作用。 常在PFC中應(yīng)用。
-
開關(guān)電源
+關(guān)注
關(guān)注
6485文章
8443瀏覽量
486144 -
變換器
+關(guān)注
關(guān)注
17文章
2120瀏覽量
110030 -
仿真
+關(guān)注
關(guān)注
50文章
4184瀏覽量
134797 -
傳遞函數(shù)
+關(guān)注
關(guān)注
0文章
102瀏覽量
14122 -
反饋
+關(guān)注
關(guān)注
3文章
44瀏覽量
4975
發(fā)布評論請先 登錄
相關(guān)推薦
.基本DC-DC變換器開關(guān)電源學習筆記
大佬都在看的開關(guān)電源學習筆記
開關(guān)電源學習筆記
開關(guān)電源學習筆記
開關(guān)電源學習筆記0 --- 初識開關(guān)電源

開關(guān)電源學習筆記 --- 目錄

開關(guān)電源學習筆記1 --- Buck變換器的基本原理

開關(guān)電源學習筆記3 --- Buck-Boost變換器的基本原理

開關(guān)電源學習筆記7 --- DC-DC變換器的儲能電感設(shè)計之磁芯及氣隙

開關(guān)電源學習筆記9 --- SPEIC變換器

開關(guān)電源學習筆記10 --- Zeta變換器

開關(guān)電源學習筆記之MOS管



















評論