很多程序員還是一個“小萌新”時就聽過這樣的說法：寫出來的代碼必須得“干凈”，為此很多人做了大量的閱讀和學習。

Redux 作者 Dan Abramov 就曾癡迷于“干凈代碼”和刪除重復代碼。多年前他和同事一起開發一個圖形編輯器畫布，當看到同事提交代碼時，他吐槽道，“這些重復代碼看起來真的很礙眼。”隨后，他自己想辦法把重復的代碼刪掉了。

“夜已深，我把改好的代碼提交到 master 分支，然后上床睡覺。因為幫同事把雜亂的代碼清理干凈了，我心里還引以為豪。”但事實并不像他想象的美好，第二天老板看到后找他談話，希望他代碼回滾回去。

當時的 Dan 很不理解，直到再工作了幾年后他才明白，除了團隊協作方面考慮，他為了減少重復代碼犧牲了靈活性。“這算不上是一個好的權衡。”他坦誠道。

無獨有偶，專門從事游戲引擎研發的資深開發者 Casey Muratori 近日也發表文章稱，那些所謂“干凈”代碼的規則“其實挺無所謂的，多數情況下也不太影響代碼的實際運行。”

這是 Casey 親自測試的結果，他表示，“認真分析就會發現，其中很多要求設置得相當隨意，難以證實或證偽。但也有一些則非常‘萬惡’，確實會影響到代碼的運行效果。”我們將 Casey 的測試分享做了翻譯，以饗讀者。

下面來看幾條有代表性的“干凈”建議：

? 相較于“if/else”和“switch”，盡量用多態；

? 不要告訴代碼它所處理的對象內部；

? 函數應該小一點；函數應該只做一件事；

? “DRY”——別重復自己。

這些要求相當具體，聽起來只要照著做了，就讓編寫出“干凈”的代碼。但問題是，這樣的代碼執行起來效果如何？

為了更確切地測試“干凈”代碼的實際表現，我決定直接用相關文獻里列出的示例代碼。這樣大家就不能說我故意黑了吧，這里只是用人家提供的現成結果來評估“干凈”代碼到底能不能打。

相信很多朋友都見過如下“干凈”代碼實例：

/* ========================================================================
   LISTING 22
   ======================================================================== */


class shape_base
{
public:
    shape_base() {}
    virtual f32 Area() = 0;
};
 
class square : public shape_base
{
public:
    square(f32 SideInit) : Side(SideInit) {}
    virtual f32 Area() {return Side*Side;}
    
private:
    f32 Side;
};
 
class rectangle : public shape_base
{
public:
    rectangle(f32 WidthInit, f32 HeightInit) : Width(WidthInit), Height(HeightInit) {}
    virtual f32 Area() {return Width*Height;}
    
private:
    f32 Width, Height;
};
 
class triangle : public shape_base
{
public:
    triangle(f32 BaseInit, f32 HeightInit) : Base(BaseInit), Height(HeightInit) {}
    virtual f32 Area() {return 0.5f*Base*Height;}
    
private:
    f32 Base, Height;
};
 
class circle : public shape_base
{
public:
    circle(f32 RadiusInit) : Radius(RadiusInit) {}
    virtual f32 Area() {return Pi32*Radius*Radius;}
    
private:
    f32 Radius;
};

這是一個基礎類，能提供幾種特定形狀：圓形、三角形、矩形、正方形。之后，它還提供一個用于計算面積的虛擬函數。

跟之前的要求一樣，這里用的是多態，函數小而且只做一件事，總之完全符合規定。于是，我們最終得到了非常“干凈”的類層次結構。每個派生的類都知道如何計算自己的面積，并存儲面積計算所需要的數據。

如果我們想要實際應用這個層次結構，比如想求輸入的所有形狀的面積總和，那大概應該是這樣：

/* ========================================================================
   LISTING 23
   ======================================================================== */
 
f32 TotalAreaVTBL(u32 ShapeCount, shape_base **Shapes)
{
    f32 Accum = 0.0f;
    for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex)
    {
        Accum += Shapes[ShapeIndex]->Area();
    }
    
    return Accum;
}

大家可能注意到了，我在這里沒有使用迭代器，因為“干凈”規則里并沒有建議要使用迭代器。為了避免對編譯器的混淆和對性能差異造成的影響，這里我決定不引入任何抽象迭代器。

另外，這個循環還基于一系列指針。這是使用類層次結構所帶來的直接結果：我們不知道這些形狀在內存里有多大，所以除非添加另外一個虛擬函數調用來獲取各形狀的數據大小、并引入某種可變的跳過操作，否則就必須要靠指針來找到各個形狀的實際起始位置。

這里做的是累加計算，所以會存在循環依賴性，這會導致循環速度下降。為了能隨意對累加進行重新排序，我還編寫了一個手填版本以確保安全：

/* ========================================================================
   LISTING 24
   ======================================================================== */
 
f32 TotalAreaVTBL4(u32 ShapeCount, shape_base **Shapes)
{
    f32 Accum0 = 0.0f;
    f32 Accum1 = 0.0f;
    f32 Accum2 = 0.0f;
    f32 Accum3 = 0.0f;
    
    u32 Count = ShapeCount/4;
    while(Count--)
    {
        Accum0 += Shapes[0]->Area();
        Accum1 += Shapes[1]->Area();
        Accum2 += Shapes[2]->Area();
        Accum3 += Shapes[3]->Area();
        
        Shapes += 4;
    }
    
    f32 Result = (Accum0 + Accum1 + Accum2 + Accum3);
    return Result;
}

如果只對這兩個例程做簡單測試，我們就能粗略測量出每個形狀完成計算所消耗的 CPU 時鐘周期：

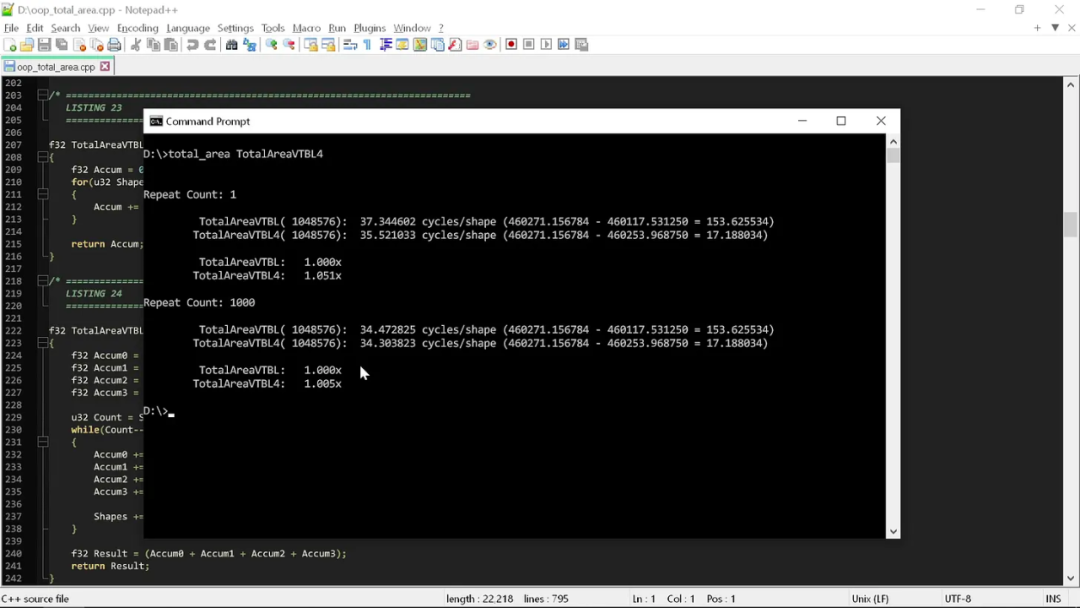
這里用兩種不同方式進行代碼測試。第一種是僅運行一次，表達“冷”狀態下的計算情況——這時數據應存留于 L3 緩存內，但 L2 和 L1 已被刷新清空，而且分支預測變量也尚未在循環中“預演”過。

第二種則是多次運行代碼，查看緩存和分支預測變量都“熱”著的時候，循環性能如何。請注意，我的這些辦法都不是真正的精準測量。大家也能看到，其中的差異如此巨大，壓根就沒必要使用嚴肅的分析工具。

從結果來看，這兩個例程沒有太大區別。“干凈”代碼在計算形狀面積時大概消耗了 35 個計算周期，如果運氣好，有時候是 34 個。也就是說，如果嚴格按照“干凈”編程的原則處理，那我們要用掉 35 個計算周期。

可如果不管第一條規矩，結果會怎樣？這里我們不使用多態，直接上 switch 語句。

我在這里編寫了完全相同的代碼，只是不再采取類層次結構的形式（也就是運行時上的 vtable），而是通過枚舉和形狀類型把所有內容都塞進了單一結構：

/* ========================================================================
   LISTING 25
   ======================================================================== */
 
enum shape_type : u32
{
    Shape_Square,
    Shape_Rectangle,
    Shape_Triangle,
    Shape_Circle,
    
    Shape_Count,
};
 
struct shape_union
{
    shape_type Type;
    f32 Width;
    f32 Height;
};
 
f32 GetAreaSwitch(shape_union Shape)
{
    f32 Result = 0.0f;
    
    switch(Shape.Type)
    {
        case Shape_Square: {Result = Shape.Width*Shape.Width;} break;
        case Shape_Rectangle: {Result = Shape.Width*Shape.Height;} break;
        case Shape_Triangle: {Result = 0.5f*Shape.Width*Shape.Height;} break;
        case Shape_Circle: {Result = Pi32*Shape.Width*Shape.Width;} break;
        
        case Shape_Count: {} break;
    }
    
    return Result;
}

這就是我們被“干凈”代碼忽悠之前，那種最老派的編程方式。

請注意，因為這里不再為各種形狀變體指定相應的數據類型，所以如果類型不具備所討論的某個值（例如「高度」），則直接忽略。

現在，這段代碼不再從虛擬函數調用中獲取面積，而是通過 switch 語句從函數中獲取——這跟“干凈”編程的原則完全不符。但大家應該看得出來，后面這種更簡潔，而且代碼并沒多大變化。Switch 語句的每種執行情況，都跟類層次結構中的相應虛擬函數有著相同的代碼。

至于加和循環本身，跟“干凈”版本也幾乎相同：

/* ========================================================================
   LISTING 26
   ======================================================================== */
 
f32 TotalAreaSwitch(u32 ShapeCount, shape_union *Shapes)
{
    f32 Accum = 0.0f;
    
    for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex)
    {
        Accum += GetAreaSwitch(Shapes[ShapeIndex]);
    }
 
    return Accum;
}
 
f32 TotalAreaSwitch4(u32 ShapeCount, shape_union *Shapes)
{
    f32 Accum0 = 0.0f;
    f32 Accum1 = 0.0f;
    f32 Accum2 = 0.0f;
    f32 Accum3 = 0.0f;
    
    ShapeCount /= 4;
    while(ShapeCount--)
    {
        Accum0 += GetAreaSwitch(Shapes[0]);
        Accum1 += GetAreaSwitch(Shapes[1]);
        Accum2 += GetAreaSwitch(Shapes[2]);
        Accum3 += GetAreaSwitch(Shapes[3]);
        
        Shapes += 4;
    }
    
    f32 Result = (Accum0 + Accum1 + Accum2 + Accum3);
    return Result;
}

唯一的區別，就是我們在這里沒有調用成員函數來獲取面積，而是調用了一個正則函數。就這么點不同。

但很明顯，與類層次結構相比，扁平結構是有很多好處的：形狀都在矩陣里，根本不需要指針。而且因為所有形狀的大小都相同，所以也不需要其他間接轉換。

另外，編譯器現在可以準確理解我們在循環中的操作，即查看 GetAreaSwitch 函數并查看整個代碼路徑。這樣，編譯器就用不著對只向運行時開放的虛擬面積函數做操作猜測。

那這些好處到底會在編譯器里轉化成怎樣的效果？這里我們一口氣把運行四種形狀，結果是：

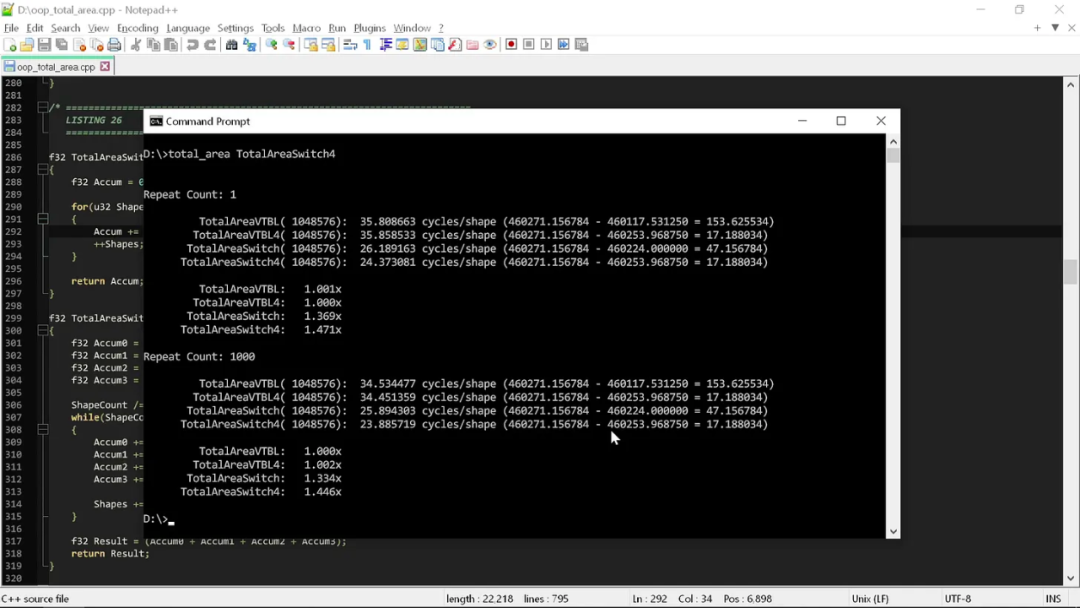
通過觀察結果，我們會發現一些很有趣的現象。單單把代碼改得“老派”一點，我們就讓性能提升了 1.5 倍。是的，別用 C++ 多態這種無關緊要的東西，性能馬上就有了改善。

通過違反“干凈”代碼原則的頭一條（也是比較核心的一條），我們把各形狀面積計算的時鐘周期從 35 個降低到 24 個。如果要拿硬件做比較，就相當于是 iPhone 14 Pro Max 降級成了 iPhone 11 Pro Max。這是三到四年的硬件演化進程，只靠不用多態就給消弭掉了。

但這還只是剛剛開始。

如果我們違反更多規矩，會怎么樣？比如說去掉第二條，“忽略對象內部”。我們能不能靠內部知識幫函數提高運行效率？

回顧一下計算面積的 switch 語句，我們會發現所有面積計算用的都是相似的方法：

        case Shape_Square: {Result = Shape.Width*Shape.Width;} break;
        case Shape_Rectangle: {Result = Shape.Width*Shape.Height;} break;
        case Shape_Triangle: {Result = 0.5f*Shape.Width*Shape.Height;} break;
caseShape_Circle:{Result=Pi32*Shape.Width*Shape.Width;}break;

也就是都在用高度乘以高度、寬度乘以寬度，需要時再乘個π之類的系數。如果是圓，那就除以 2。

這就是我跟“干凈”代碼原則最不對付的地方，我覺得 switch 語句很棒！它能向我們清晰地展示這些模式，因為在按操作（而不是按類型）進行代碼組織時，可以很直觀地發現其中的常規模式。相比之下，再看“干凈”編程示例，我們可能永遠發現不了這樣的模式。那邊不僅樣板更多，而且倡導者建議把每個類都放進單獨的文件里。

所以從結構上講，我一般不贊成使用類層次結構。總而言之，現在我想強調最重要的一點——我們可以通過觀察模式，來大大簡化這條 switch 語句。

請記住：這個示例不是我選的。這是“干凈”代碼自己選的說明示例。而且跟面積計算類似，其他很多任務也有相似的算法結構。要想利用這種模式，我們可以整理一個簡單的表，用于說明每種類型所對應的系數。如果我們將圓形和矩形等設定為單參數類型，就可以寫出更簡單的求面積函數：

/* ========================================================================
   LISTING 27
   ======================================================================== */
 
f32 const CTable[Shape_Count] = {1.0f, 1.0f, 0.5f, Pi32};
f32 GetAreaUnion(shape_union Shape)
{
    f32 Result = CTable[Shape.Type]*Shape.Width*Shape.Height;
    return Result;
}

這里的兩個求和循環不用做多大修改，除了只能調用 GetAreaUnion（而非 GetAreaSwitch），其余部分完全相同。

下面來看看這個版本的運行性能如何：

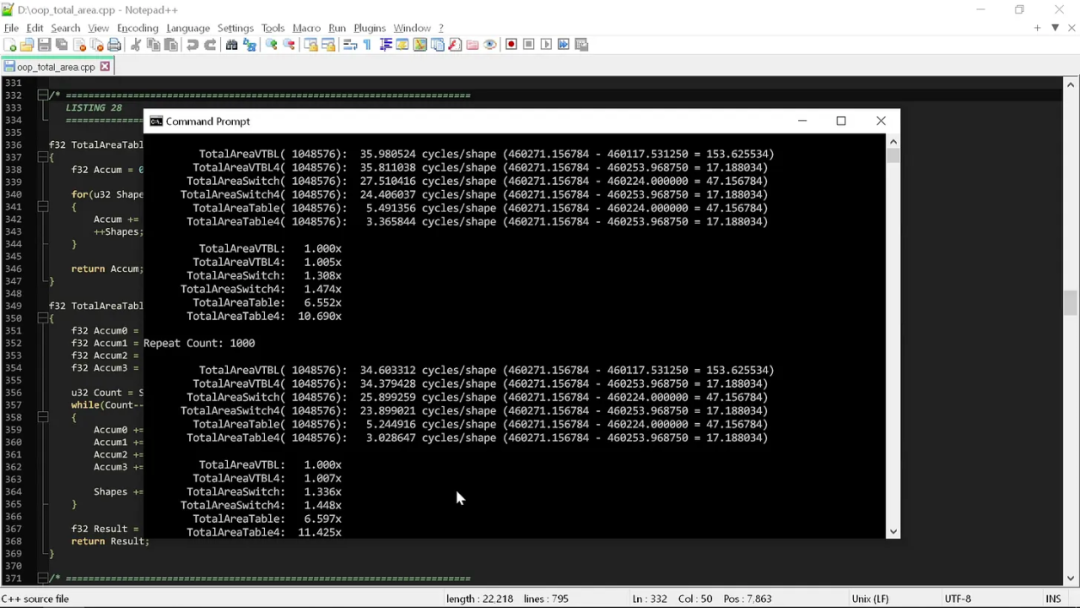
可以看到，通過對實際類型的理解，我們有效將基于類型的思路轉換成了基于函數的思路，從而大大提高了速度。跟之前的 iPhone 相比，現在我們的計算速度已經相當于登陸了臺式機。

而我們唯一所做的，就是一次表查找加一行代碼，沒別的了！這樣不僅更快，在語義上也更簡單。它涉及的 token 更少、操作更少、代碼行數也更少。

所以說，我們有必要把數據模型跟計算操作結合起來，而不是要求什么“忽略內部”。現在，我們對每個形狀的面積計算只消耗 3.0 到 3.5 個計算周期。

放棄前兩條“干凈”編程規則，已經讓我們的代碼性能提升了 10 倍。

10 倍性能提升絕對非同小可，畢竟就連多年之前推出的 iPhone 6（現代性能基準測試所能支持的最老機型），其性能也只是 iPhone 14 Pro Max 的三分之一。

如果用單線程桌面 CPU 性能來比較，那 10 倍的差距就相當于拿現在的 CPU 跟 2010 年的產品對抗。看到了吧，單是前兩條“干凈”編程規則，就消滅了這 12 年來的硬件演變成果。

更令人震驚的是，恢復這部分性能的操作如此簡單。這里我們沒有強調“函數要小”和“函數只做一件事”這兩條，畢竟我們這個測試很簡單，天然符合這些規定。那么，如果我們在問題里再加個要求，應該就能看到它們的實際影響了吧？

這里，我在原有層次結構之上又添加了一個虛擬函數，用于給出各個形狀有幾個角：

/* ========================================================================
   LISTING 32
   ======================================================================== */
 
class shape_base
{
public:
    shape_base() {}
    virtual f32 Area() = 0;
    virtual u32 CornerCount() = 0;
};
 
class square : public shape_base
{
public:
    square(f32 SideInit) : Side(SideInit) {}
    virtual f32 Area() {return Side*Side;}
    virtual u32 CornerCount() {return 4;}
    
private:
    f32 Side;
};
 
class rectangle : public shape_base
{
public:
    rectangle(f32 WidthInit, f32 HeightInit) : Width(WidthInit), Height(HeightInit) {}
    virtual f32 Area() {return Width*Height;}
    virtual u32 CornerCount() {return 4;}
    
private:
    f32 Width, Height;
};
 
class triangle : public shape_base
{
public:
    triangle(f32 BaseInit, f32 HeightInit) : Base(BaseInit), Height(HeightInit) {}
    virtual f32 Area() {return 0.5f*Base*Height;}
    virtual u32 CornerCount() {return 3;}
    
private:
    f32 Base, Height;
};
 
class circle : public shape_base
{
public:
    circle(f32 RadiusInit) : Radius(RadiusInit) {}
    virtual f32 Area() {return Pi32*Radius*Radius;}
    virtual u32 CornerCount() {return 0;}
    
private:
    f32 Radius;
};

矩形有四個角，三角形有三個角，圓形一個角都沒有。之后，我要調整問題的定義，從計算各形狀的總面積轉為計算各形狀的角加權面積和——也就是總面積再加上角總數。

跟總面積一樣，算這個角加權面積沒有任何實際意義，單純是為了演示性能差異，用的也是最簡單的數學計算。

這里，我用數學計算和其他虛擬函數調用更新了“干凈”求和循環：

f32 CornerAreaVTBL(u32 ShapeCount, shape_base **Shapes)
{
    f32 Accum = 0.0f;
    for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex)
    {
        Accum += (1.0f / (1.0f + (f32)Shapes[ShapeIndex]->CornerCount())) * Shapes[ShapeIndex]->Area();
    }
    
    return Accum;
}
 
f32 CornerAreaVTBL4(u32 ShapeCount, shape_base **Shapes)
{
    f32 Accum0 = 0.0f;
    f32 Accum1 = 0.0f;
    f32 Accum2 = 0.0f;
    f32 Accum3 = 0.0f;
    
    u32 Count = ShapeCount/4;
    while(Count--)
    {
        Accum0 += (1.0f / (1.0f + (f32)Shapes[0]->CornerCount())) * Shapes[0]->Area();
        Accum1 += (1.0f / (1.0f + (f32)Shapes[1]->CornerCount())) * Shapes[1]->Area();
        Accum2 += (1.0f / (1.0f + (f32)Shapes[2]->CornerCount())) * Shapes[2]->Area();
        Accum3 += (1.0f / (1.0f + (f32)Shapes[3]->CornerCount())) * Shapes[3]->Area();
        
        Shapes += 4;
    }
    
    f32 Result = (Accum0 + Accum1 + Accum2 + Accum3);
    return Result;
}

基本上就是整體接入另一個函數，添加了新的間接層。同樣是出于明確起見，這里不用任何抽象。

在 switch 語句那邊，我做的變更也基本相同。先是給角數量添加另一條 switch 語句，跟層次結構版本可以說是完美對應：

/* ========================================================================
   LISTING 34
   ======================================================================== */
 
u32 GetCornerCountSwitch(shape_type Type)
{
    u32 Result = 0;
    
    switch(Type)
    {
        case Shape_Square: {Result = 4;} break;
        case Shape_Rectangle: {Result = 4;} break;
        case Shape_Triangle: {Result = 3;} break;
        case Shape_Circle: {Result = 0;} break;
        
        case Shape_Count: {} break;
    }
    
    return Result;
}

下面看看這兩個版本的計算性能差異：

/* ========================================================================
   LISTING 35
   ======================================================================== */
 
f32 CornerAreaSwitch(u32 ShapeCount, shape_union *Shapes)
{
    f32 Accum = 0.0f;
    
    for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex)
    {
        Accum += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[ShapeIndex].Type))) * GetAreaSwitch(Shapes[ShapeIndex]);
    }
 
    return Accum;
}
 
f32 CornerAreaSwitch4(u32 ShapeCount, shape_union *Shapes)
{
    f32 Accum0 = 0.0f;
    f32 Accum1 = 0.0f;
    f32 Accum2 = 0.0f;
    f32 Accum3 = 0.0f;
    
    ShapeCount /= 4;
    while(ShapeCount--)
    {
        Accum0 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[0].Type))) * GetAreaSwitch(Shapes[0]);
        Accum1 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[1].Type))) * GetAreaSwitch(Shapes[1]);
        Accum2 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[2].Type))) * GetAreaSwitch(Shapes[2]);
        Accum3 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[3].Type))) * GetAreaSwitch(Shapes[3]);
        
        Shapes += 4;
    }
    
    f32 Result = (Accum0 + Accum1 + Accum2 + Accum3);
    return Result;
}

跟之前的求總面積類似，類層次結構和 switch 兩種實現之間的代碼基本相同。唯一的區別，就是調用虛擬函數還是使用 switch 語句。

再來看表驅動的示例，這種把計算操作跟數據結合起來辦法真的棒。而且這個版本需要修改的只有表里的值。我們甚至不需要獲取關于形狀的其他信息，只要把角數跟面積系數直接加進表中，就能用幾乎相同的代碼得出結果：

/* ========================================================================
   LISTING 36
   ======================================================================== */
 
f32 const CTable[Shape_Count] = {1.0f / (1.0f + 4.0f), 1.0f / (1.0f + 4.0f), 0.5f / (1.0f + 3.0f), Pi32};
f32 GetCornerAreaUnion(shape_union Shape)
{
    f32 Result = CTable[Shape.Type]*Shape.Width*Shape.Height;
    return Result;
}

如果運行所有“角面積”函數，就能看到第二個形狀的屬性如何影響其性能：

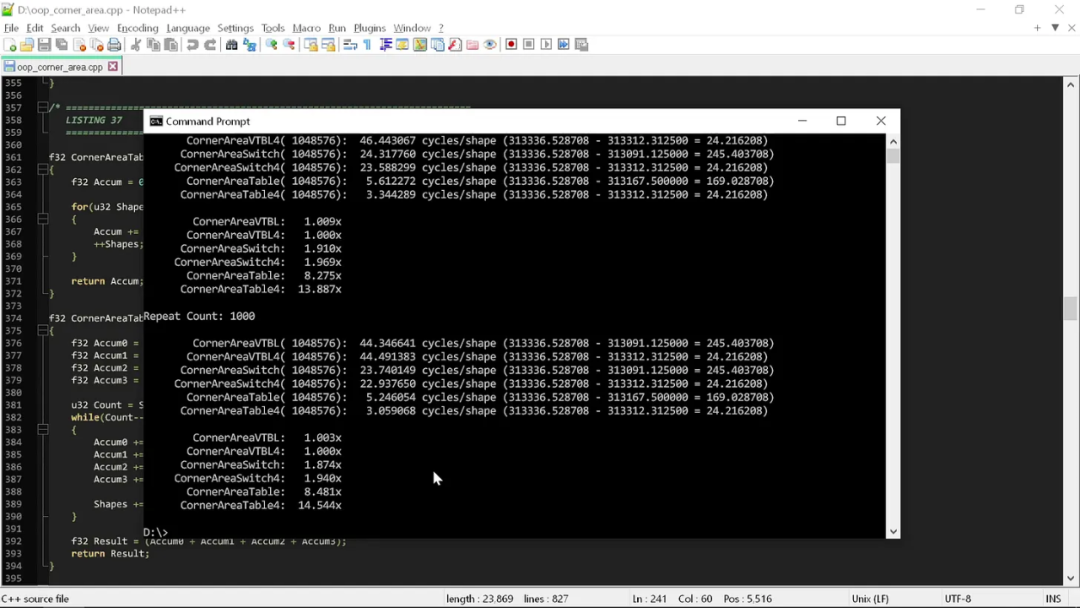
可以看到，這次測試中“干凈”代碼的表現更差。Switch 語句的性能達到了“干凈”版本的 2 倍，而查表版本更是達到后者的 15 倍。

這也凸顯出“干凈”代碼的深層次問題：需求越復雜，這些規矩就越有損性能。當我們把這種“干凈”編程方法引入各種真實用例時，最終性能肯定會大打折扣。

而且“干凈”代碼用得越多，編譯器就越理解不了你想干什么。一切都被放進了單獨的翻譯單元，被藏在虛擬函數調用之后。這樣即使編譯器再聰明，也難以消化這混亂的實現。

更可怕的是，這樣的代碼連人看了都會束手無策！從之前的演示中可以看到，如果代碼庫圍繞著函數進行架構設計，那么從表中取值或者刪除 switch 語句等需求才會易于實現；而如果是圍繞類型進行架構設計，那難度將大大增加。唯一的解決辦法，恐怕就只有大規模重寫。

總之，只是在形狀計算中增加了一個屬性，速度差就從 10 倍變成了 15 倍，相當于硬件性能從 2023 年一下子倒退回了 2008 年！一個參數，抹滅 14 年硬件發展，是不是很大膽？而且，咱們還完全沒涉及優化呢。

之前的所有演示，都只是在拿循環依賴關系做文章，完全沒提有哪些優化空間。下面，我們來看相同計算流程在經過輕度優化后的 AVX 版本：

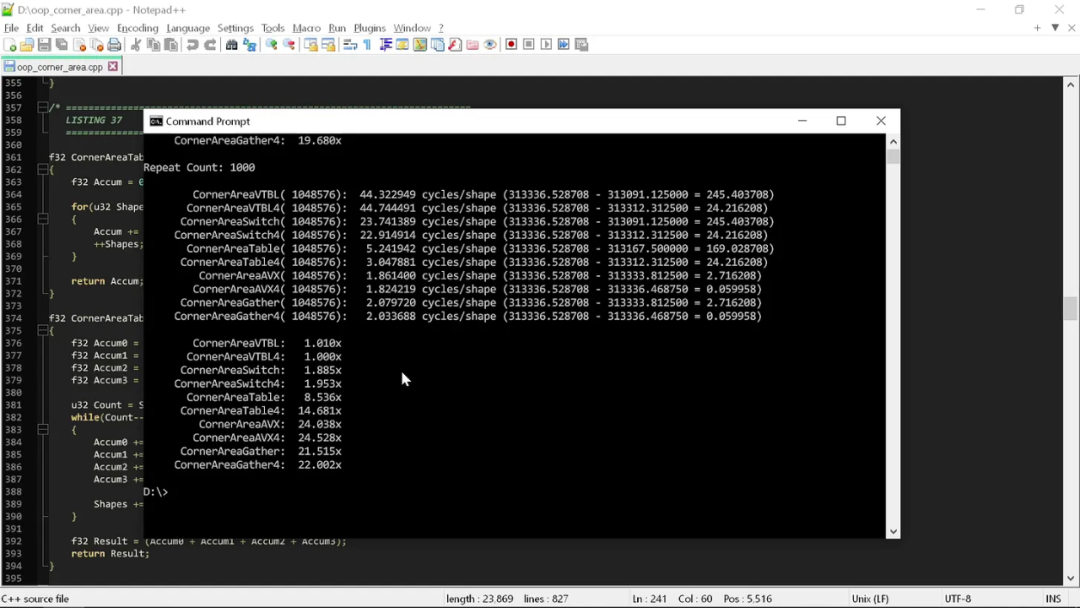
速度差異到了 20 到 25 倍區間。當然，AVX 優化的代碼完全不理會“干凈”編程的那些奇談怪論。五大原則已經祛魅了四條，再來看最后一條。

老實講，“不要重復自己”其實是有道理的。我們拿來測試的版本也沒有多少重復部分。只有 4 次累加的部分算是重復，但這是為了演示。畢竟如果是在真實應用當中，我們甚至沒必要把它分成 2 個例程。

如果把“不要重復自己”說得更具體點，比如不要把相同系數的兩個編碼版本分別構建成兩個表，那我還可以反對一下。畢竟有時候這樣能獲得更好的性能。但人家沒那么講，只是說別自我重復，那這話還是相當合理的。

最重要的是，我們完全可以在遵循第五條的同時保持合理的代碼性能。

所以我現在給出結論：在這五條原則里，只有最后一條值得遵循，前面四條可以統統無視。為什么？大家可能注意到了，現在的軟件運行起來真的越來越慢。跟現代硬件的真實性能相比，軟件的運行表現太差了。

要問為什么這么慢，那答案可就多了，而最核心的因素要視實際開發環境和編程方法而定。但至少從特定角度出發，“干凈”代碼絕對有著不可推卸的責任。雖然其底層邏輯都說得通，但造成的性能負擔卻是我們難以承受的。

所以面對這種種規矩，盡管有人認為這樣能改善代碼庫的可維護性，但我們至少也該想想背后的代價是什么。

我們真的愿意放棄這十幾年的硬件發展，只為讓程序員的工作變得更輕松一點嗎？我們的職責就是開發出能順暢在硬件上運行的程序。如果這些原則嚴重影響了軟件的運行效果，那豈不背離了我們的從業初衷？

當然，我們仍然可以繼續探索更好的代碼組織、維護改進和易讀性方法，這些都是非常合理的訴求。但“干凈”編程的這些規矩不是，它們根本就不靠譜。我強烈建議他們能用大星號標明“采取這些規則，您的代碼性能將縮水十幾倍”。

審核編輯 ：李倩