1. 控制原理

1.1 開環與閉環系統

下面是開環系統與閉環系統的示例。以給水壺加熱的過程舉例，開環系統只是簡單的利用開關信號控制水壺的加熱。

而下圖的閉環控制系統中，將添加溫度傳感器所測量的信號作為系統的反饋量。設計控制系統的核心就是通過對閉環系統的控制器進行調整，利用反饋量信號，完成閉環的穩定控制。

同時，這就是反饋的過程。

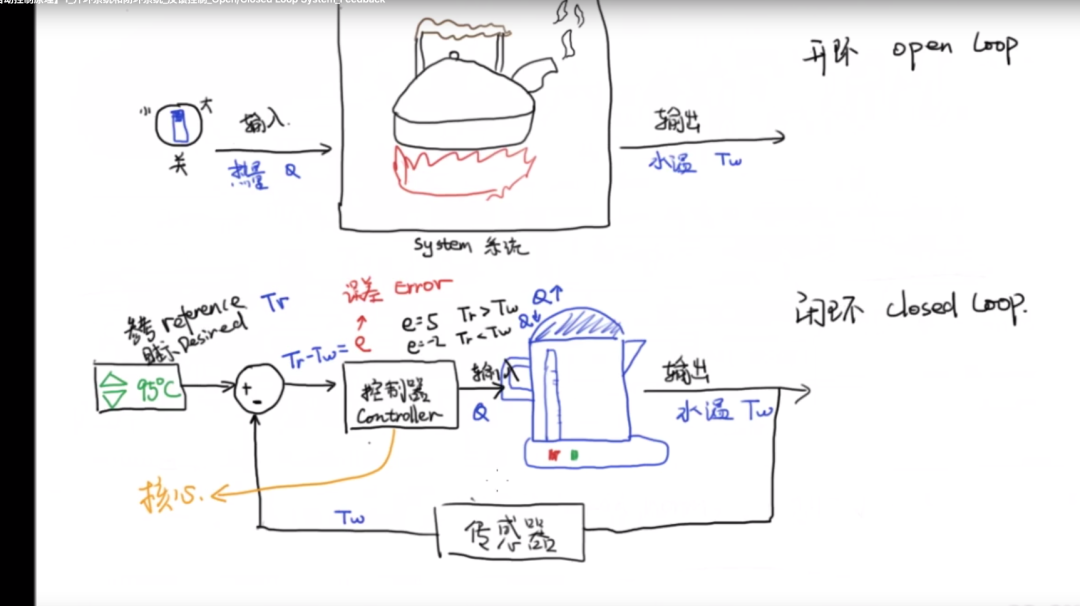
簡單的開環系統有如下描述：（這里以流體力學的公式作為舉例）

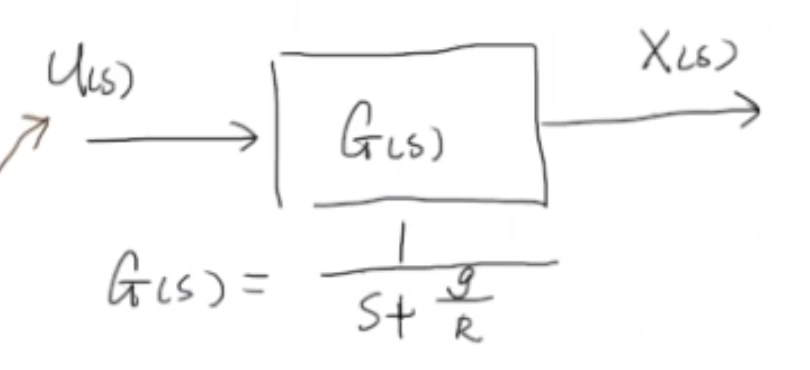
添加控制器D(s)，并增加測量H(s)，構成如下閉環系統。

但是在分析閉環系統的穩定性時，一般的做法是將其轉換成為開環系統，并將新構造的開環系統傳遞函數作為研究對象，分析系統的穩定性。

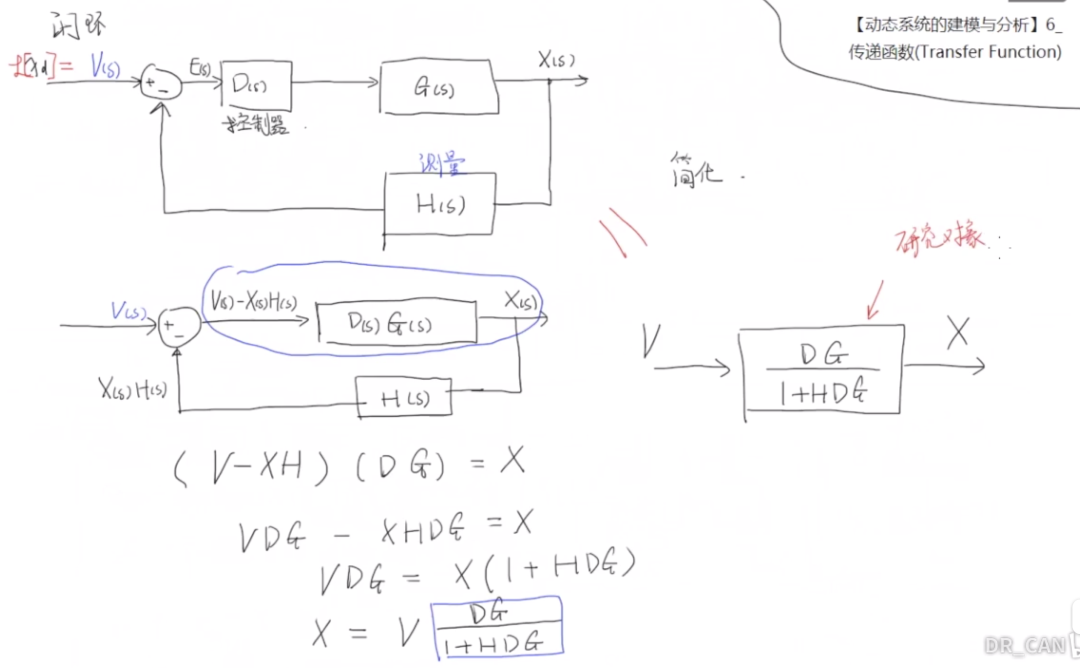
1.2 穩定性分析

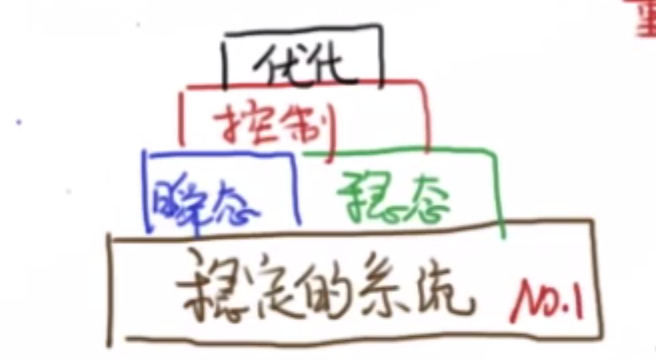
對于一個系統，如果沒有穩定性的先決條件，那么其他的（穩態誤差分析、瞬態誤差分析）將無從說起。穩定性：傳遞函數極點在復平面的左半邊。（橫坐標為極點，縱坐標為零點）

所以對于系統穩定性的討論，實際上是在分析輸入為單位沖激函數時，系統輸出的傳遞函數。最后觀察系統輸出隨時間變化的曲線是否到達穩定的位置。

零點和極點的定義如下：

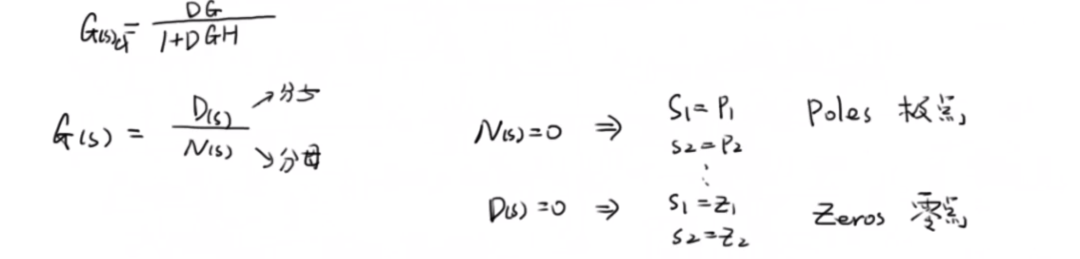
分析為什么極點為負的，系統是穩定的：

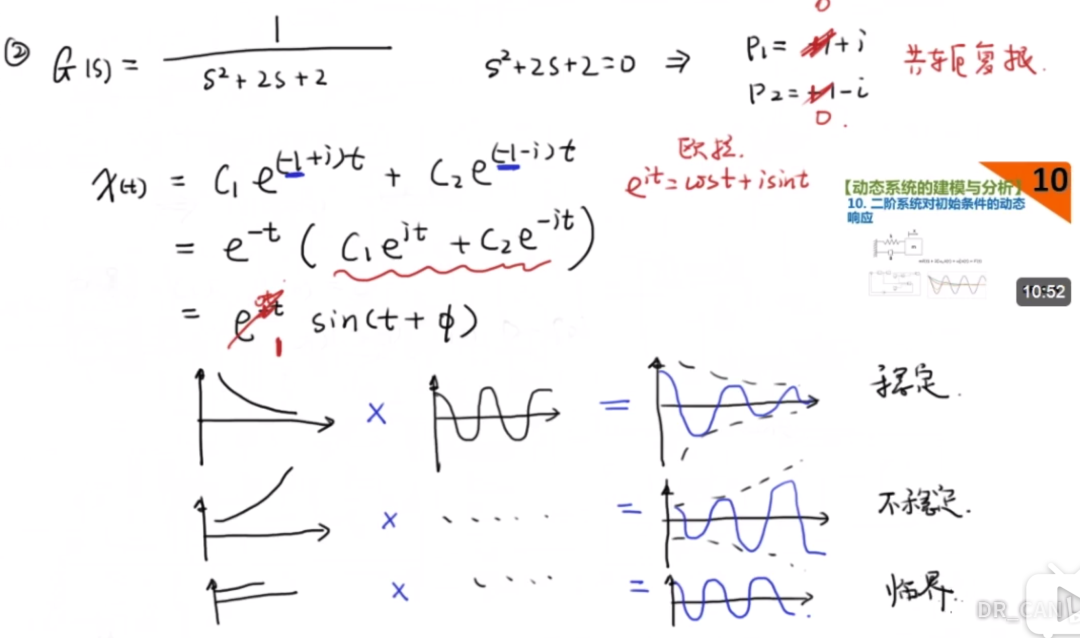
下面這個圖要更加直觀：

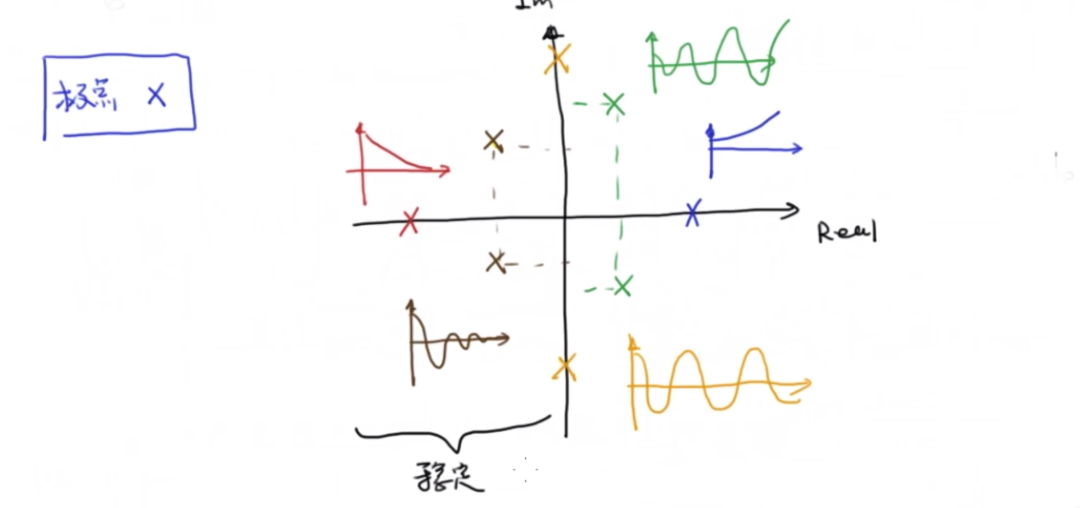
那么我們如何設計控制器？就是將最終的傳遞函數的極點在左邊平面，叫做極點配置。現代控制理論中，研究的是狀態矩陣的特征值，對應的就是傳遞函數的極點。

1.3 一起燃燒卡路里/科學減肥（系統分析實例_數學建模部分）

框圖表示如下：

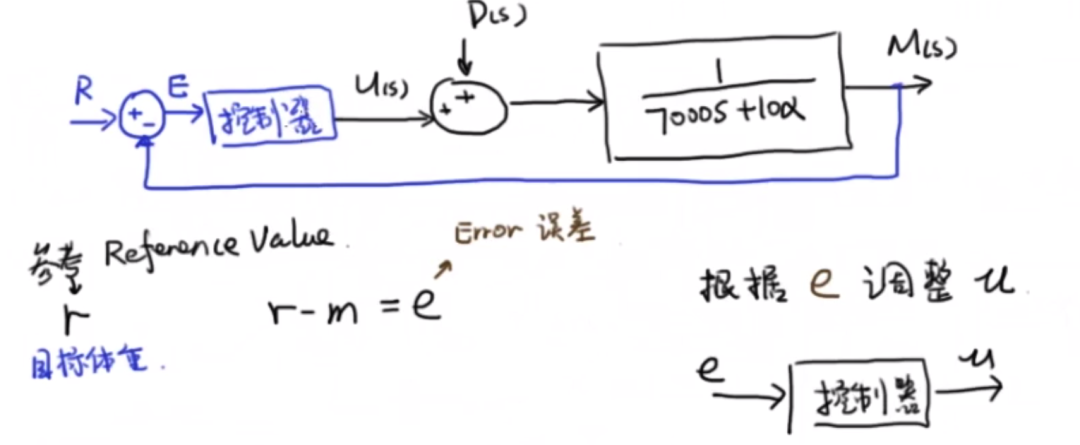
設計比例控制器（最為簡單的控制器）如下：

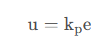
那么如何設計該控制器，讓最終的系統趨向于穩定狀態呢？（也就是說傳遞函數的極點在左半邊平面）

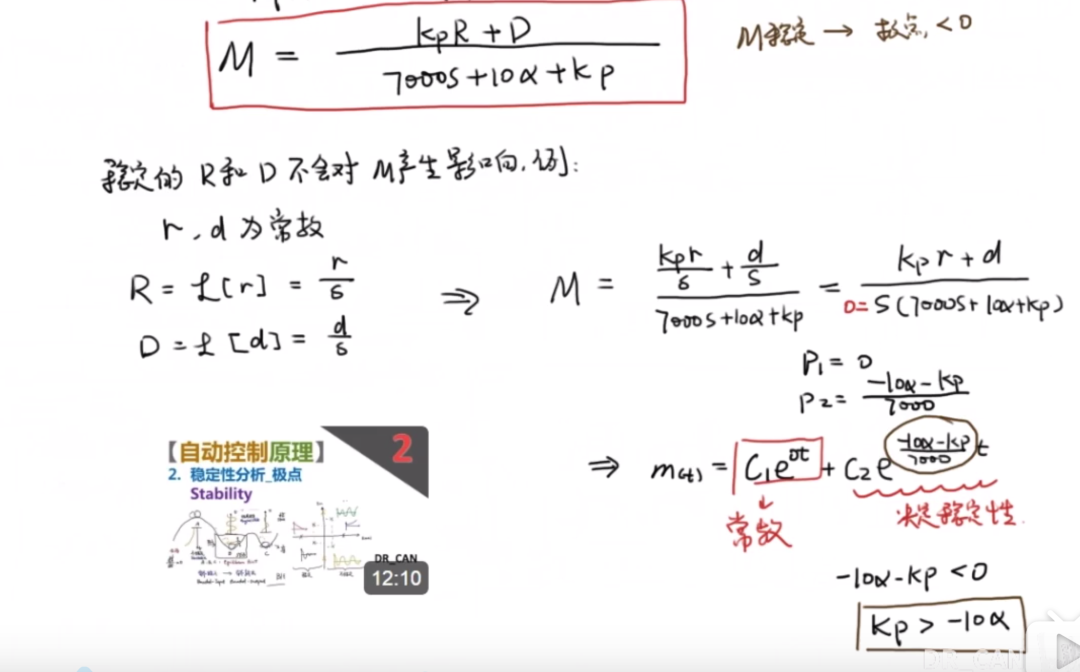
學習控制理論一定要從微分方程入手，弄清楚微分方程與傳遞函數之間的關系就會容易理解很多。

通過對于比例控制器的分析之后發現，單純的比例控制最終產生穩態誤差。

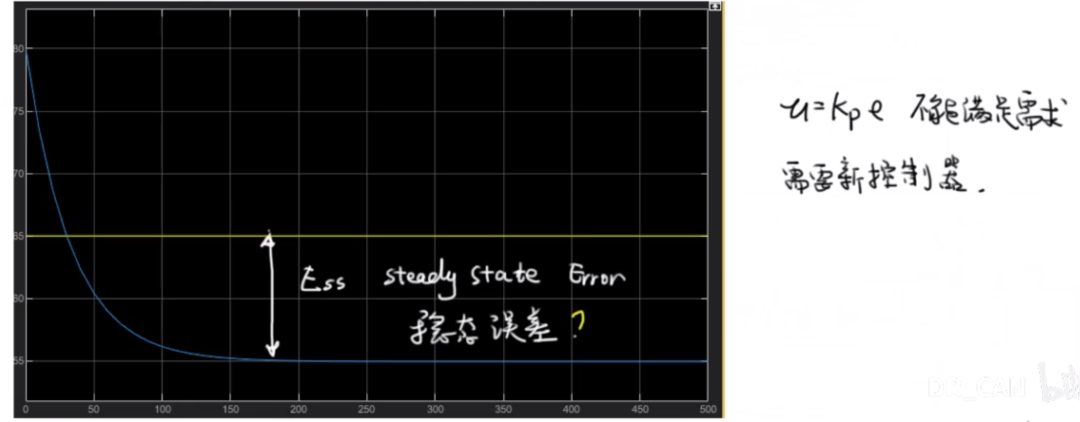
1.4 終值定理與穩態誤差

下面討論的系統是存在參考信號的系統，類似于下圖。終值定理，用來算系統輸出的極限的工具。（FVT）

下圖解釋了彈簧阻尼系統的傳遞函數，還有在沖激響應下系統的終值定理的使用方式。

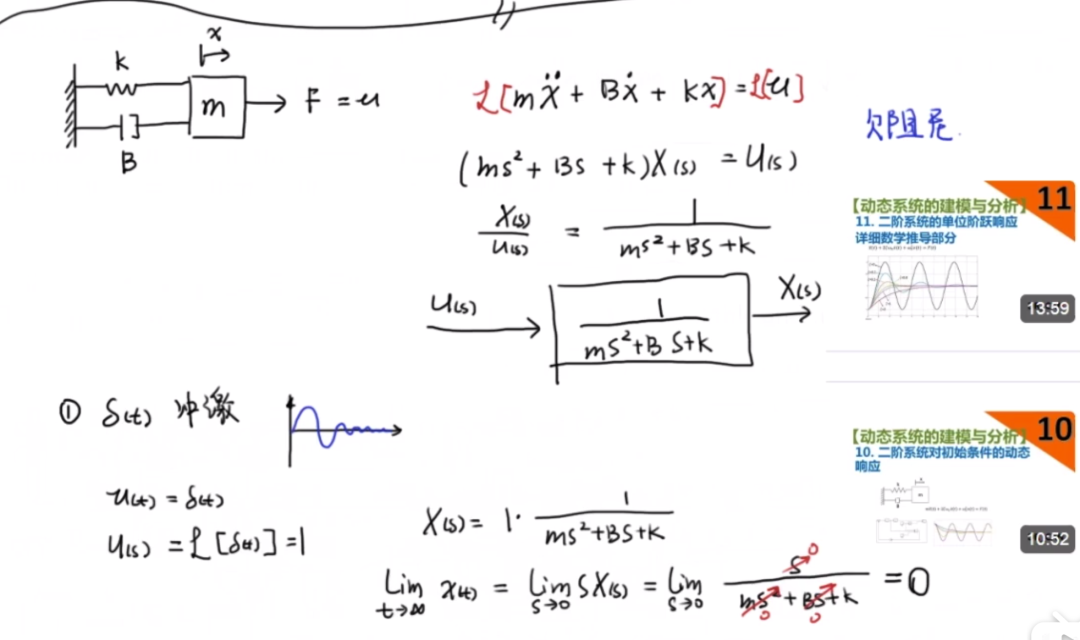
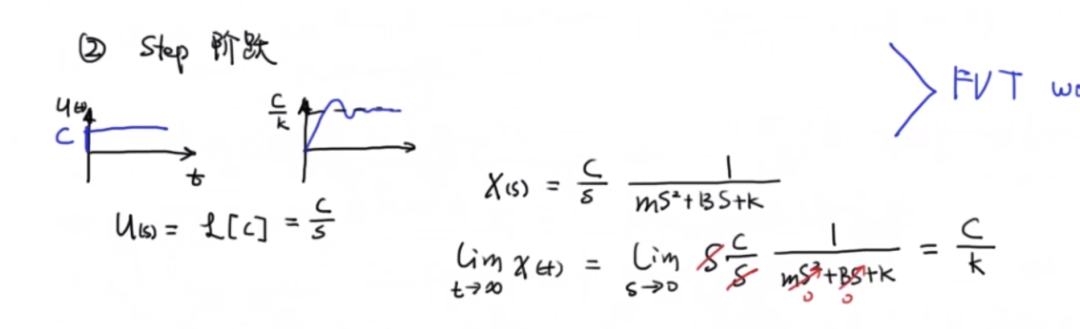
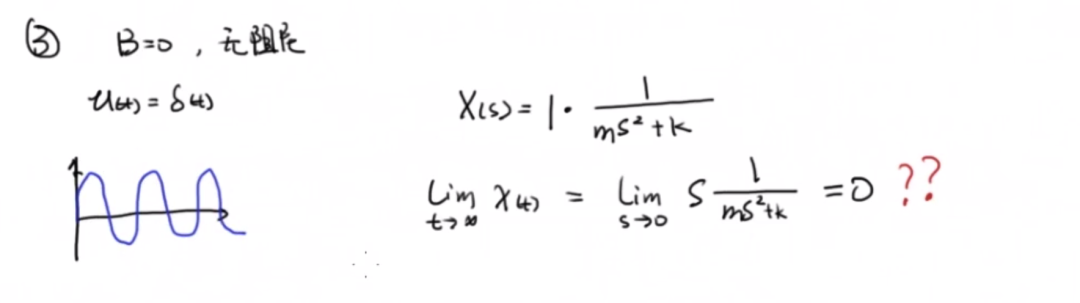
這里需要注意的是第二種情況，代表了輸入參考信號為c時（相當于r）的情況。

條件如下：

最終求出來的極限值經過運算就是系統的穩態誤差。

1）比例控制

舉例說明。下面是一個最為簡單的一階系統，采用的控制方式是比例控制。

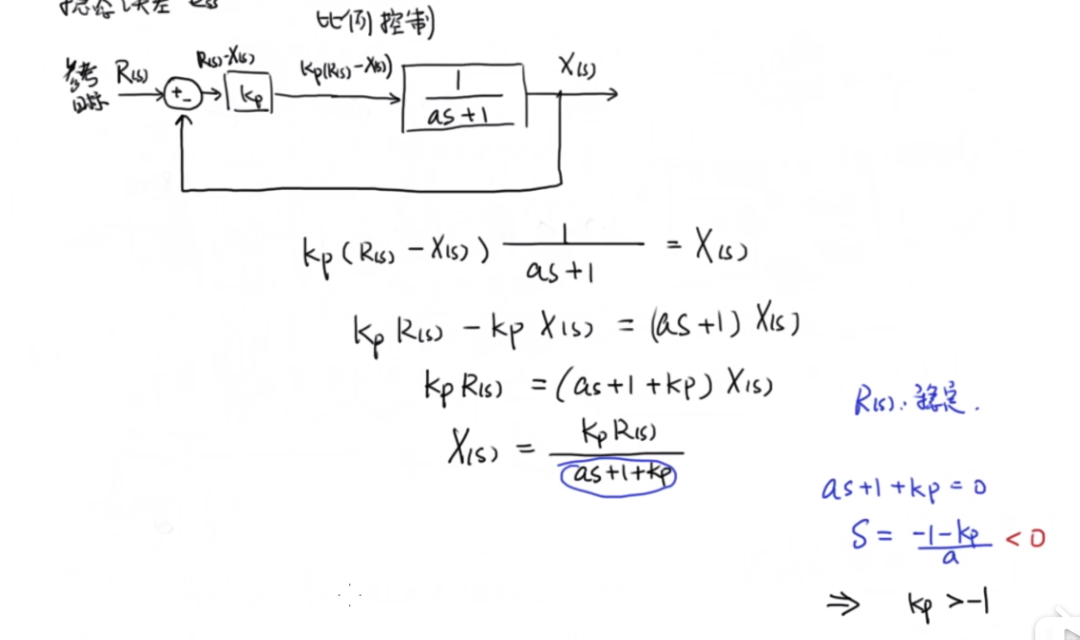
利用定理分析穩態誤差如下：

這里說明了比例控制的局限性，必須采用更加實用性的控制算法。比例控制充法消除穩態誤差

2）比例積分控制

并有下面變換方式：

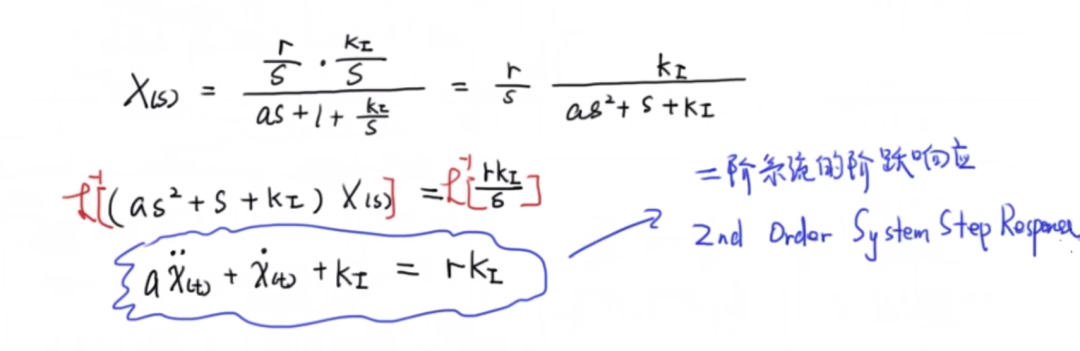
通過引入一個積分信號，讓本來的一階系統變成一個二階系統。

1.5 根軌跡

再回到彈簧系統，是一個二階系統。

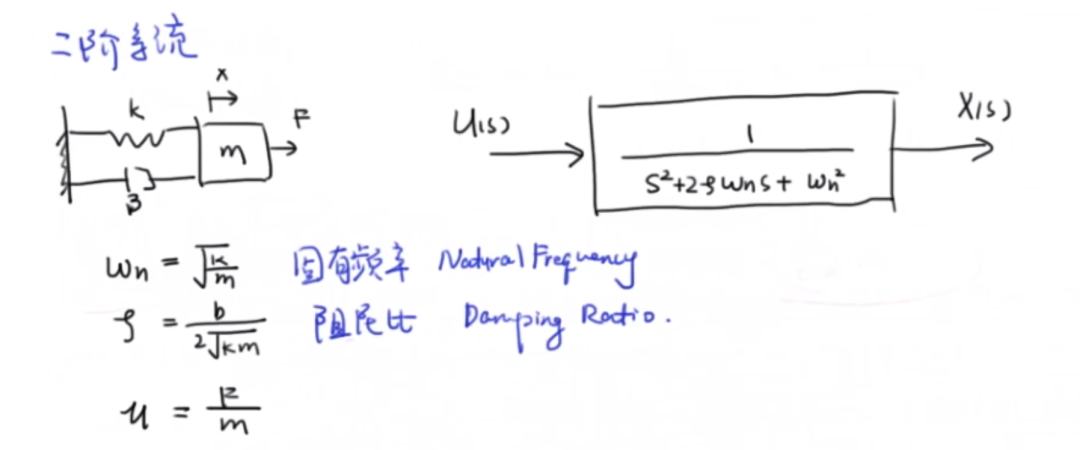
對于高階系統不過也是幾個一階系統的疊加，如下：

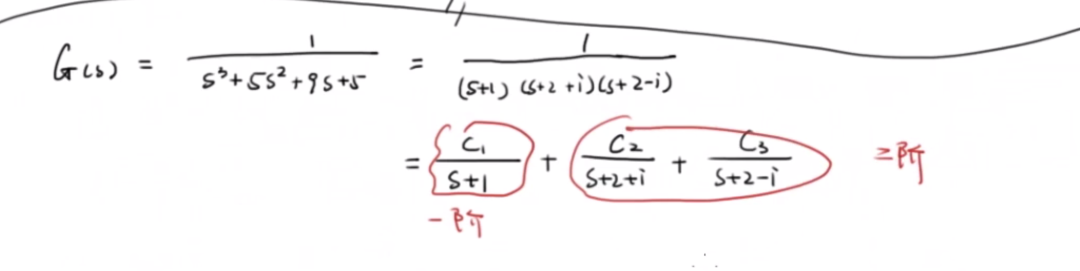
這一節評估了根的位置對于控制器的影響。

1.6 PID控制

比例控制

微分控制：調節水溫變化的速度，

積分控制：誤差的累計量

注意：

比例積分控制沒有單獨的比例控制收斂快

微分控制解決了超調量問題

微分控制的問題是初始狀態下的輸入值很大

同時，微分控制的控制量受到測量誤差的影響非常大。他對噪聲非常敏感

2. 數學工具

2.1 拉普拉斯逆變換

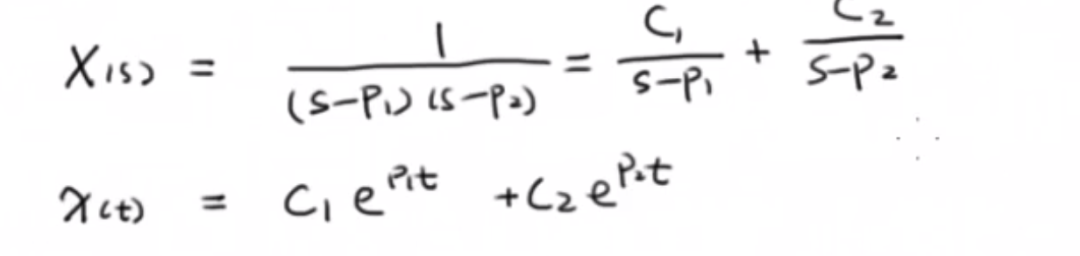
2.2 矩陣的性質

矩陣有下面的性質，現代控制理論的分析中常常會用到。

2.3 bode圖

給信號濾波的過程中，需要注意幅頻響應。如果在帶通范圍內不是1的話，就會改變信號的幅值，就會改變最終加速度輸出的信號。

另外，上面的圖就是bode圖，但是是基于離散系統的。

如何去理解bode圖？

bode圖是針對于傳遞函數而言的，用在連續系統上。（因為控制系統常常用傳遞函數來表示。）

%% 這個是正解b = [1,2,3];a = [2,1,3];figure;bode(b,a)% [h1 , ftp] = freqs(b,a);mag = 20*log10(abs(h1)); % get magnitude of spectrum in dBphase = angle(h1)/pi*180; % get phase in deg.figuresemilogx(ftp,mag)xlabel('Frequency (Hz)'),ylabel('Magnitude (dB)')

（這樣描述是和真實系統不一致的，具體參考濾波器性質）

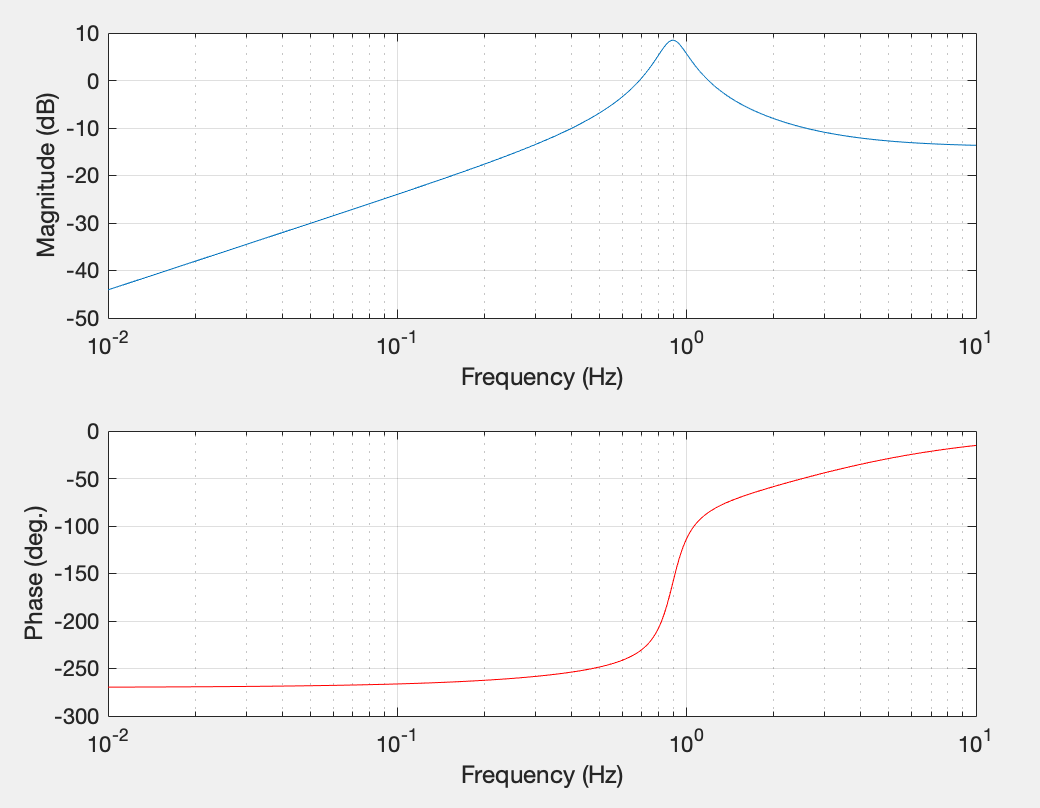
總結來說有以下幾點：

振幅的比較用10log10就行，但是能量的比較需要20log10

振幅與功率/能量之間的關系如下：

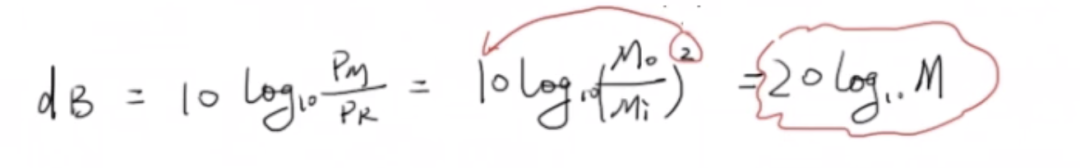
從一個實例出發理解bode圖

對于系統傳遞函數：

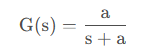
分析頻率響應：

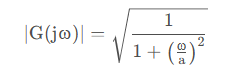
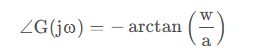
低頻：w<

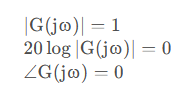
截止頻率：w=a

這個-3dB很重要，表達的是輸出的振幅是輸入的振幅的sqrt(1/2)，能量是一半的關系。

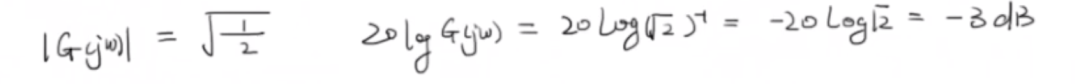
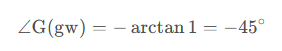
高頻：w>>a

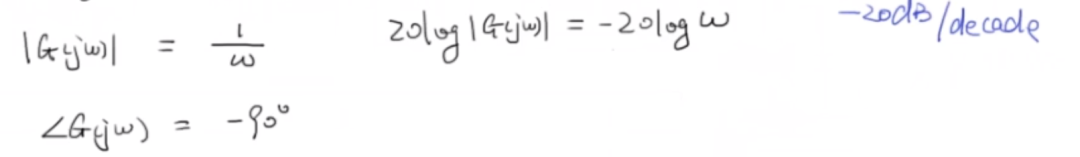
bode圖如下：

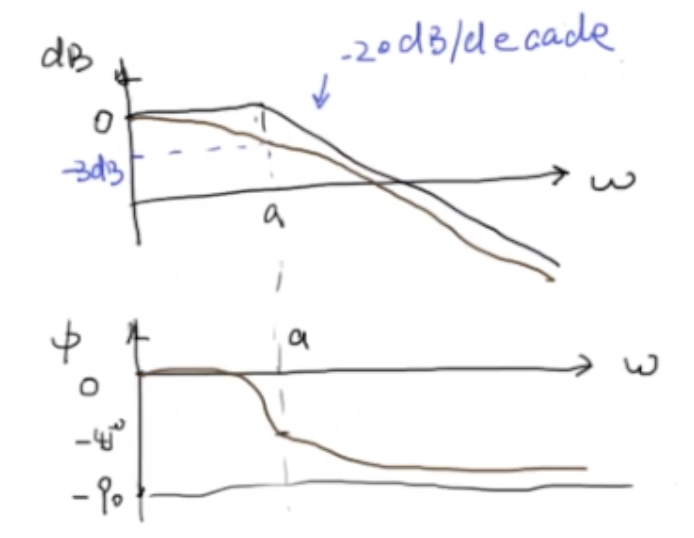
bode圖的作用是什么？

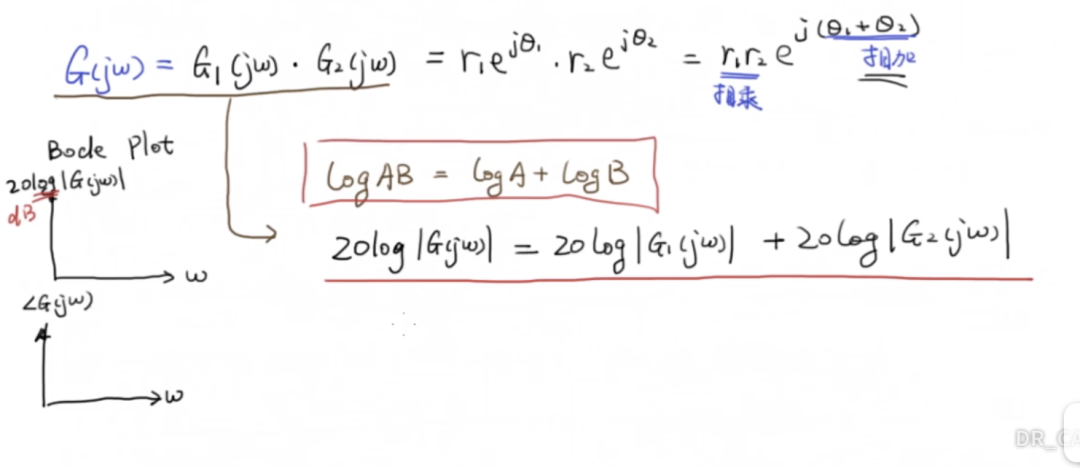
實際上，我們可以將級聯系統的子系統bode圖進行累加，那么我們就得到了新的級聯系統的真正的bode圖了。原理如上。

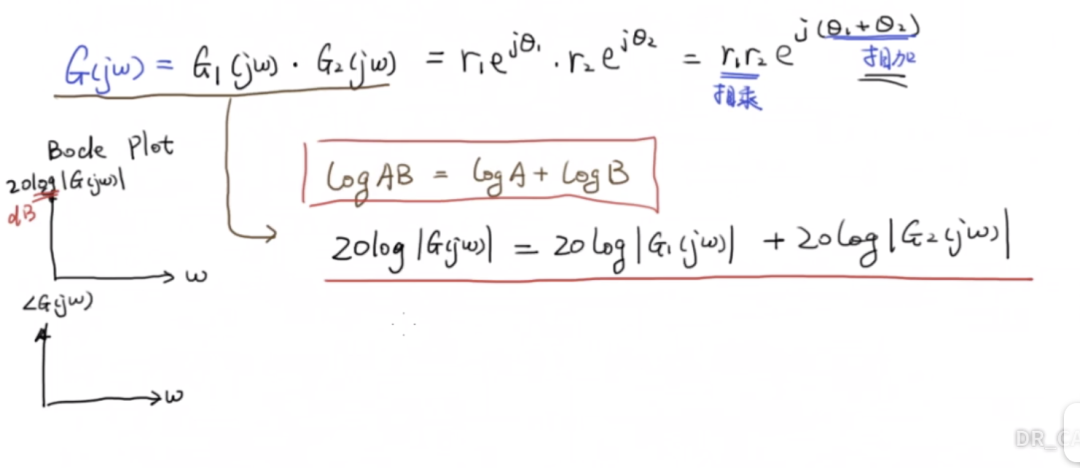
2.4 單位沖激函數

三. 現代控制原理串講

1. 現代控制理論概要

首先要了解一個簡單的彈簧阻尼模型，作為控制的對象，其滿足胡克定律。

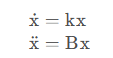
描述現代控制理論中的系統，最基礎的當然是狀態空間表示法：

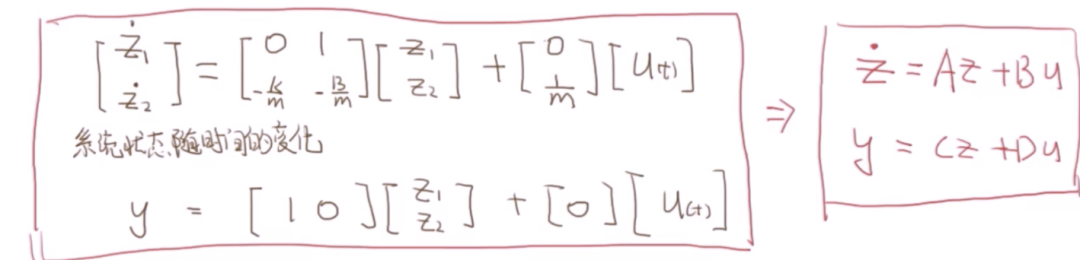
當然，通過拉普拉斯變換可以轉換成下面的形式，控制對象是彈簧阻尼塊。

其中有一條重要的信息，實際上矩陣A的特征值就是G(s)的極點，決定了系統的穩定性。上面的右式時通用的。

去分析一個系統，主要需要考慮以下幾個重要的性質。

（那么對于自動控制，只需要極點就夠了）

可控性

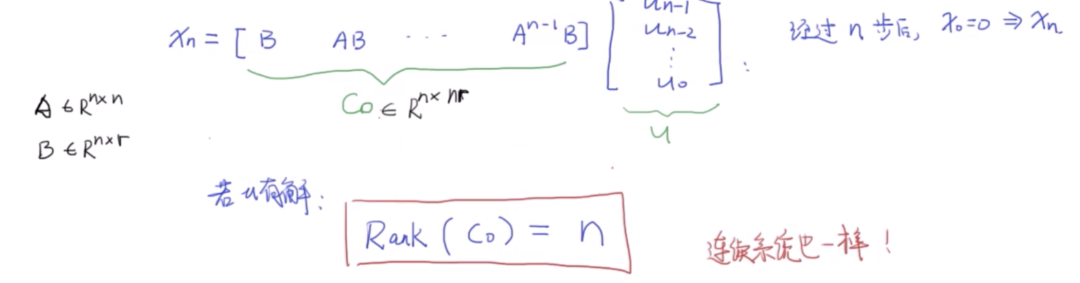
李雅普諾夫穩定性：確定系統的穩定狀態，控制系統可以滿足數學的條件。在一階系統中，常常用極點分析的方法去觀察穩定性。現代控制理論中常用到的分析系統的方法就是去找系統的V函數，得到最后是不是能夠

可觀性：狀態觀測器。系統狀態加入不可直接測量，那么就需要通過輸出和控制量去估計狀態。狀態觀測器需要達到一個收斂的狀態。建立觀測器時，實際上是建立一個反饋系統，使得誤差等于0。（這里是不是有誤差狀態量的部分？）

對于可觀測性，需要問一個問題：是不是所有系統都是可測的？借鑒可控性的推導，有下面的結論：

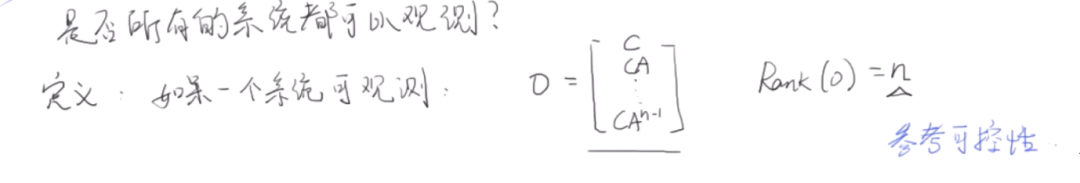
2. 怎樣去分析一個狀態空間方程系統呢？

實際上看到設計控制器就是去配置特征值的過程。這里的特征值有點像自動控制原理中的極點的概念，決定了系統隨時間是收斂的，還是振動的，還是逼近于無窮的。

下面是對于一個控制系統的分析過程，利用配置特征值的方法可以確定比例控制的控制系數u與狀態量x之間的關系。

四. 最后的一些思考

軌跡跟蹤與制導之間的關系

軌跡跟蹤的目標是使狀態和參考狀態的誤差保持在0附近。舉例，對深空飛行器而言，按照軌跡優化+軌跡跟蹤這兩個步驟實現控制。

參考軌跡是人為設計的，可以是全局最優的，也可以是次優的。然后把跟蹤誤差保持在0附近，這也有一套控制律，比如LQR軌跡跟蹤器。

狀態控制按照給定的控制律，在航天器軌跡控制中叫做制導；在姿態控制中好像沒見過先設計好姿態運動規律的，都是即時控制。

制導律必須全局漸進穩定，適用于高動態的環境，比如空空導彈采用比例導引法。