四虎在线视频观看,亚洲欧美久久婷婷爱综合一区天堂 ,一个人在线观看www免费视频

0.前言

寄存器是CPU中的稀有資源，如何高效的分配這一資源是一個至關重要的問題。本文介紹了基于圖著色的寄存器分配算法。

寄存器分配看似離我們很遙遠，實際上在我們的生活中就有類似的問題，例如為每個班級分配上課的教室就與寄存器分配有著相似性。

其中班級相當于程序中的變量，教室相當于寄存器。在同一個時間段上課的兩個班級不能分配到一個教室，對應于寄存器分配就是兩個同時活躍的變量不能分配同一個寄存器。

可見寄存器分配是一個非常有趣且值得研究的問題。

1. 為何進行寄存器分配

Fig 1.1 內存層次圖

從上面的Fig 1.1的圖中可以看到，計算機系統(tǒng)的內存共分為四個層次：寄存器、緩存、內存、硬盤。

實際上數據在這四種形式的內存中的移動由三個對象負責管理，這三個對象分別是應用程序、硬件、編譯器。

應用程序只負責管理數據在內存和硬盤之間的移動，其它形式的內存對應用程序而言是透明的。
硬件負責管理數據在內存和緩存之間的移動。
編譯器負責管理數據在寄存器和內存之間的移動。

而CPU的運算速度遠高于內存的存取速度，其中寄存器與CPU的通信速度最快，所以合理的利用寄存器，能夠提高程序的效率。這也是為啥寄存器分配在編譯器中屬于非常重要的一部分。

2 算法總架構

整個算法分為多個步驟，每個步驟相對來說較為復雜，對于每一步會單獨分一個小節(jié)介紹。在單獨介紹每一步之前，先來看一下寄存器分配的總流程圖

Fig 2.1 寄存器分配流程圖

Make_Webs()函數

多個相交的du鏈形成一個網，Make_Webs函數用來發(fā)現du鏈中所有的網。

Build_AdjMtx()函數

沖突圖需要用一個二維的鄰接矩陣表示，該鄰接矩陣的下三角表示兩個寄存器是否沖突。AdjMtx[i,j] = true表示符號寄存器(或真實寄存器)i與j相互沖突。

Coalesce_Regs()函數

使用鄰接矩陣合并寄存器。會搜索賦值指令例如 Si = Sj這樣的指令，而且要滿足Si與Sj不相互沖突（AdjMtx[i,j]的值為false）。如果找到這樣的指令，就會將對Sj的定義改為對Si的定義，并刪除改賦值指令。如果執(zhí)行了寄存器合并，則跳轉到1繼續(xù)執(zhí)行，如果沒有則進行下一步

Build_AdjLsts()函數

構建一個鄰接表，其中的每一個元素表示一個符號寄存器，記錄了與符號寄存器相關的信息。鄰接表用一個數組AdjLsts[1..nwebs]表示，數組中的每一個元素是一個listrecd記錄。

Compute_Spill_Cost函數

計算每個符號寄存器溢出到內存和從內存恢復到寄存器的開銷。

Prune_Graph()

使用degree

Assign_Regs()

根據鄰接表的信息給每個節(jié)點著色，不相鄰的兩個節(jié)點可以有相同的顏色。如果成功則執(zhí)行Modify_Code()將符號寄存器換為真實寄存器。如果著色失敗，則執(zhí)行下一步

Gen_Spill_Code

將符號寄存器溢出到內存，產生相應的store/load指令。如果重建該值的開銷小于溢出，也可重新計算該值，而不是溢出到內存。然后返回到步驟1

Modify_Code

如果步驟7成功，則執(zhí)行Modify_Code,將分配的顏色替換為實際的寄存器。

算法的偽代碼如下：

do
  do
    Make_Webs();
    Build_AdjLsts();
    C = Coalesce_Regs();
  while !C
  
  Build_AdjLsts();
  Compute_Spill_Costs();
  Prune_Graph();
  Succ = Assign_Regs();
  
  if Succ
    Modify_Code();
  else
    Gen_Spill_Code();
while Succ

接下來的每一小節(jié)是對每個步驟的具體介紹。

3.構建web

網是寄存器分配的對象。使用網而不是變量做為寄存器分配的對象是因為同樣的變量名可能在程序重復使用，但這些同名變量卻毫不相關。

例如一個程序中會多次使用i做為多個for循環(huán)中的循環(huán)變量，但這些for循環(huán)其實是不相關的。

網的定義：多條相交的du鏈屬于同一個網，即多個du鏈有一個共同的use。

具體的web例子如下：

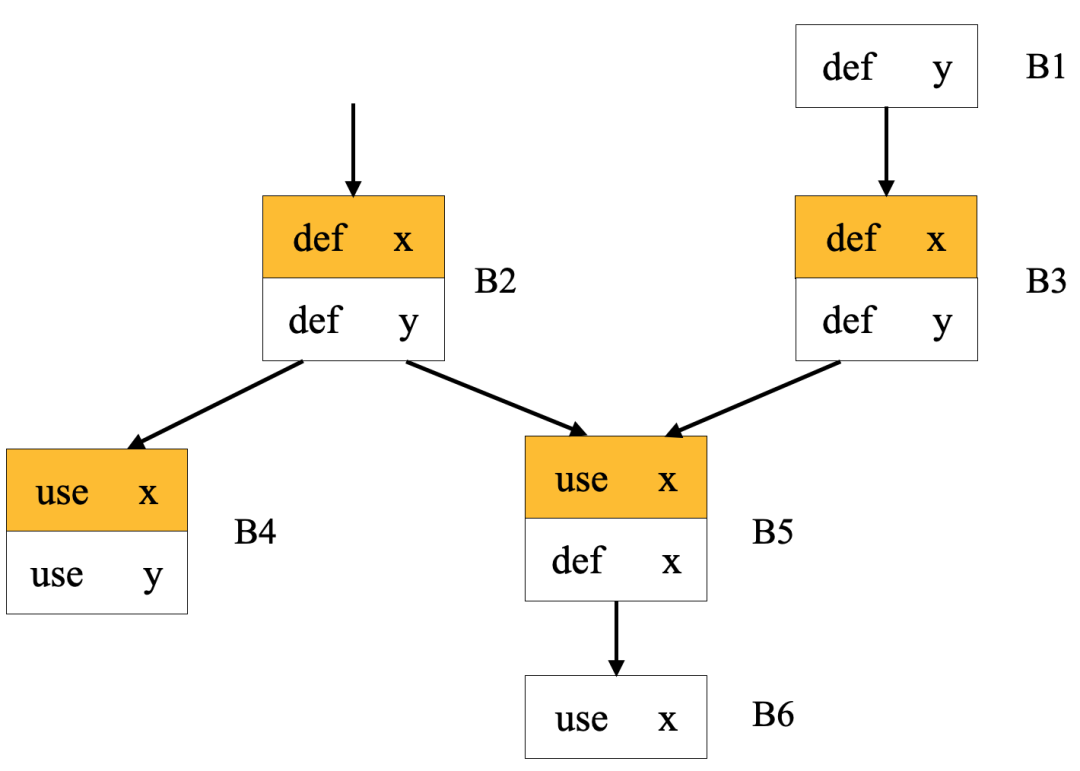
Fig 3.1 多個web構成的一個webs

圖中的黃色部分是最復雜的一個網（下表中的W1)，即兩條du鏈有共同的use，因此這兩條du鏈構成一個網。

圖中共有四個網，具體如下表

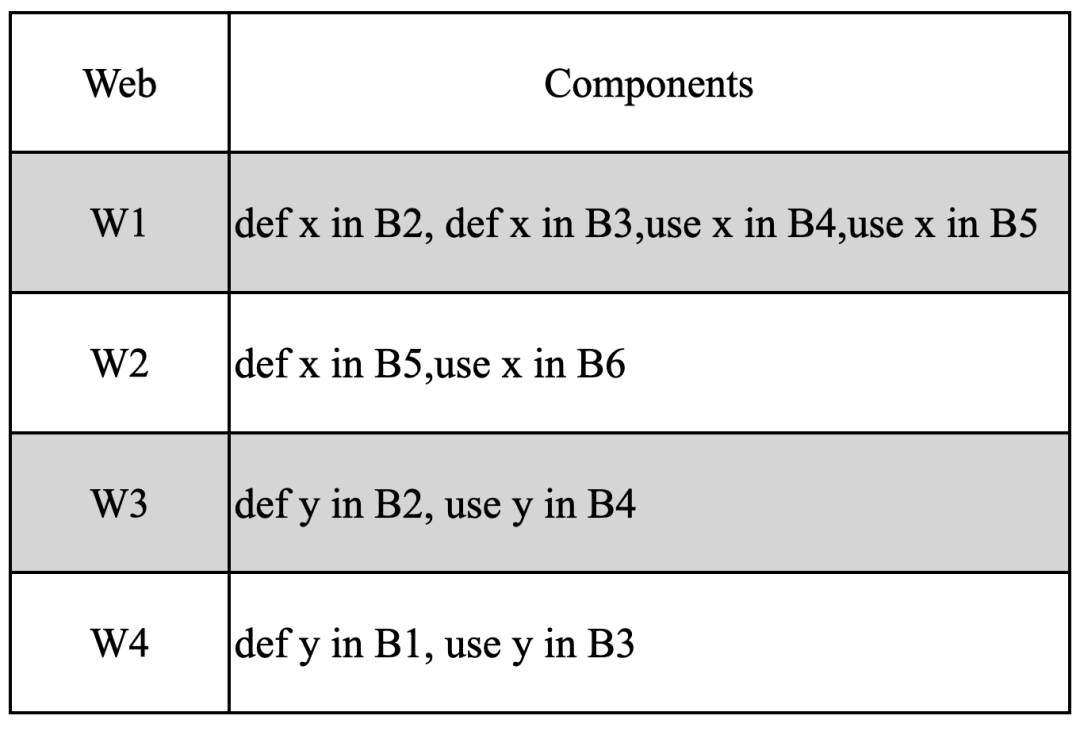
Fig 3.2 來自Fig 3.1的網

du鏈在算法中的類型為UdDuChain，由一個三元組組成，s表示一個符號，p表示s所表示的符號的def所在的位置，Q表示該符號use的集合。

可以通過下面的例子來熟悉du鏈在算法中的表示

黃色部分第一條du鏈用如下符號表示：

<<x,

即x在B2中的第一條指令處定義，在B4和B5中的第一條指令處都有使用。

黃色部分第二條du鏈

<<x,

兩條du鏈在中有共同的use，因此兩條鏈最終構成一個網：

{
<<x,

如果用sdu表示類型為UdDuChain的一條du鏈，則sdu@1表示符號s，sdu@2表示def所在的位置p，sdu@3表示use集合Q

<<x,

對于上圖的du鏈，sdu@1表示x，sdu@2表示def 。

sdu@3表示use集合{,}即x在和處都有使用。

弄清楚了每個符號的含義，看懂下面的算法實現就容易了。

首先是webs的初始化，將每個du鏈視為一個web。

//用du鏈初始化web
for each sdu in DuChains{
    nwebs += 1;
    webs U= {

需要注意的是，U= 表示求并集，代碼中symb:sdu@1表示將sdu@1賦值給symb。

然后是將有共同use的du鏈合并到一起形成web。

do{
    oldnwebs = nwebs;
    TmpWebs1 = Webs;
    while(TmpWebs1 != null){
        // #號表示從TmpWebs1中取出一個web
        web1 = #TmpWebs1;
        TmpWebs1 -= {web1};
        TmpWebs2 = TmpWebs1;
        while(TmpWebs2 != null){
            web2 = #TmpWebs2;
            TmpWebs2 -= {web2};
            if( web1.symb = web2.symb &&
                ( web1.uses - web2.uses) != null)
            {
              web1.defs U= web2.defs;
              web1.uses U= web2.uses;
              webs -= {web2};
              nwebs -= 1;
            }
        }
    }
}while(oldnwebs!=nwebs)

一句話概括算法主要思想：在TmpWebs1中取其中一個網記作web1，除去web1后剩下的網組成TmpWebs2，并在TmpWebs2中取一個網記作web2，如果web1與web2有共同的use，則合并web1與web2，直到TmpWeb1s為空為止。

最后是將webs中的每一個web和真實寄存器放到同一個數據結構SymReg[i]中

// 1到nregs為真實寄存器
for( i = 1 to nregs){
    Symreg[i] = {

4. 構建沖突圖

沖突圖在算法中用鄰接矩陣和鄰接表這兩種數據結構來表示。

鄰接矩陣用來表示兩個節(jié)點之間是否相互沖突，而鄰接表用來表示每個節(jié)點的一些其他信息。

以如下代碼為例構建沖突圖：

s1 = 2;//row 1
s2 = 4;//row 2
s3 = s1 + s2;//row 3
s4 = s1 + 1;//row 4
s5 = s1*s2;//row 5
s6 = s4*2//row 6

假定有三個寄存器r1，r2，r3可用，且s4不能存儲在r1中。

上述程序的沖突圖如下：

Fig 4.1 沖突圖

圖中的邊表示兩個符號寄存器存在沖突，即兩個符號寄存器不能分配到同一個真實寄存器中。s4與r1的邊表示s4不能分配到r1。

本節(jié)中鄰接表和鄰接矩陣的建立都是以上面的這個沖突圖為例。

4.1 建立鄰接矩陣

Fig 4.2 鄰接矩陣表示沖突圖

圖Fig 4.2是用矩陣表示圖Fig 4.1中的沖突圖。true表示兩個節(jié)點相互沖突，false表示兩個節(jié)點沒有沖突。

鄰接矩陣在算法中用一個二維數組AdjMtx[i,j]表示。AdjMtx的初始化代碼如下：

//注意i從2開始取是因為Fig 4.2中的行是從r2開始
for i =2 to nwebs{
    for j = 1 to i-1{
        //下三角全部初始化為false
        AdjMtx[i,j] = false;
    }
}
//任何兩個真實寄存器之間相互沖突
for i = 2 to nregs{
    for j = 1 to i-1{
        AdjMtx[i,j] = true;
    }
}

初始化后對于兩個沖突的節(jié)點i與j對應的AdjMtx[i,j]需要置為true。具體算法如下。

函數Interfere用來判斷符號寄存器與真實寄存器是否存在沖突。函數Live_At用來判斷兩個符號寄存器之間是否沖突。

for i = nregs to nwebs{
  for j = 1 to nregs{
      if Interfere(Symreg[i],j){
          AdjMtx[i,j] = true;
      }
  }
  
  for j = nregs+1 to i-1{
      for each def in Symreg[i].defs{
          if Live_At(Symreg[j],Symreg[i].symb,def){
              AdjMtx[i,j] = true;
          }
      }
  }
}

4.2 建立鄰接表

除了鄰接矩陣之外還需要用鄰接表記錄鄰接矩陣中每個元素的一些相關信息。鄰接表中的每個元素也代表了每個寄存器的信息，包括真實寄存器和符號寄存器。

鄰接表用一個數組表示，數組的每個元素是一個結構體，共六個字段，分別是color, disp, spcost,nints, adjnds, rmvadj。

color表示該節(jié)點的顏色
disp表示該符號寄存器溢出到內存的地址
nints表示與該節(jié)點相互沖突節(jié)點的個數
adjnds是一個鏈表，保存了與當前節(jié)點相互沖突的所有節(jié)點
rmadj也是一個鏈表，保存了移除的部分節(jié)點，這些移除的節(jié)點也是與當前節(jié)點相沖突的

下圖是用來表示Fig 4.1中沖突圖的一個鄰接表。

Fig 4.3 表示Fig 4.1的初始化鄰接矩陣

鄰接表的初始化代碼如下：

for i = 1 to nregs{
  AdjLsts[i].nists = 0;
  AdjLsts[i].color = -Max;
  AdjLsts[i].disp = -Max;//-Max表示負無窮
  AdjLsts[i].spcost = Max;//Max表示正無窮
  AdjLsts[i].adjnds = null;
  AdjLsts[i].rmvadj = null;
}

for i = nregs + 1 to nwebs{
  AdjLsts[i].nists = 0;
  AdjLsts[i].color = -Max;
  AdjLsts[i].disp = -Max;
  AdjLsts[i].spcost = 0.0;
  AdjLsts[i].adjnds = null;
  AdjLsts[i].rmvadj = null;
}

for i = 2 to nwebs{
  for j = 1 to i-1{
      if AdjMtx[i,j]{
          AdjLsts[i].nists += 1;
          AdjLsts[i].adjnds += [j]
          AdjLsts[j].nists += 1;
          AdjLsts[j].adjnds += [i]
      }
        
  }
}

5.寄存器合并

對于賦值指令來說，實際上應該把兩個寄存器當做一個來處理，這實際上也是復寫傳播的一個變種。

Sj = Si//類似于這種只有兩個寄存器的賦值指令

當兩個寄存器出現在賦值指令的兩端而且兩個寄存器不存在相互沖突，并且兩個寄存器在賦值指令到程序結束沒有被賦值，可以將這兩個寄存器在相互合并(合并鄰接表和鄰接矩陣)。

具體操作分四步：

查找Sj = Si 這樣的賦值指令，滿足Si與Sj互不沖突，且Si與Sj到程序結束沒有賦值，如果找到則進行下面步驟
尋找向Si賦值的指令，將Si改為Sj
移除賦值指令Sj = Si
調整鄰接矩陣表示的沖突圖，以及合并Si與Sj所在的網。

for i = 1 to nblocks{
  for j =1 to ninsts[i]{
    if LBlock[i][j].kind = regval
      //獲取Si = Sj 指令的左邊的寄存器號Si
      k = Reg_to_Int(LBlock[i][j].left);
      //獲取Si = Sj 指令的右邊的寄存器號Sj
      l = Reg_to_Int(LBloclk[i][j].opd.val);
      //步驟1
      if !AdjMtx[max(k,l),min(k,l)] && Non_Store(LBlock,k,l,i,j)
      {
           for p = 1 to nblocks{
             for 1 =1 to ninsts[p]{
               if LIR_Has_Left(LBlock[p][q])&&
                  LBlock[p][q] == LBlock[i][j]
                  {
                    //步驟2
                    LBlock[p][q].left = LBlock[i][j].left
                  }
              }
           }
           //步驟3
           delete_inst(i,j,ninsts,LBlock,Succ,Pred);
           //步驟4
           Symreg[k].defs U= Symreg[l].defs;
           Symreg[k].uses U= Symreg[l].uses;
           //調整鄰接矩陣,直接將最后面的節(jié)點覆蓋掉合并后不需要的l節(jié)點。
           Symreg[l] = Symreg[nwebs];
           for p = 1 to nwebs{
             if AdjMtx[max(p,l),min(p,l)]
               AdjMtx[max(p,k),min(p,k)] = true;
             else
               AdjMtx[max(p,l),min(p,l)] = AdjMtx[nwebs,p]
           }
           nweb -= 1;//合并后web的數量減1
          
       }
  }
}

需要注意的是代碼中AdjMtx[max(k,l),min(k,l)]中的 max(k,l)出現在矩陣的下標是因為我們是用下三角來表示沖突圖的，而且行號要比列號大，具體參照Fig 4.2表示的鄰接矩陣就明白了。

6. 計算溢出開銷

將符號寄存器的值溢出到內存的目的是為了讓所有的變量都有地方保存，當寄存器的數量不夠時，就需要將符號寄存器的值溢出到內存。

將符號寄存器的值溢出到內存，可以減少沖突圖中某個節(jié)點與其它節(jié)點沖突的數量，從而使整個沖突圖可以R著色。

溢出的開銷通常用一個公式來計算，這個公式也是啟發(fā)式的，通常使用如下公式。

其中def、use、copy分別是網w中的各個定值、使用和寄存器復制，defwt、usewt、copywt是對應的權重。

具體代碼如下：

//Compute_Spill_Costs函數的具體實現
for i = 1 to nblocks
{
  for j = 1 to ninsts[i]
  {
    inst = LBlock[i][j]
    switch(LIR_Exp_Kind(inst.kind))
    {
      //二元表達式
      case binexp:
           //操作數1的類型是寄存器編號
           if inst.opd1.kind == regno
              //depth(i)表示循環(huán)的層數
              AdjLsts[inst.opd1.val].spcost] += UseWt*10^depth(i);
           if inst.opd2.kind == regno
              AdjLsts[inst.opd1.val].spcost] += UseWt*10^depth(i);
           break;
      //一元表達式
      case unexp:
           if inst.opd.kind == regno
              if inst.kind == regval
                 AdjLsts[inst.opd.val].spcost -= CopyWt*10^depth(i);
              else
                 AdjLsts[inst.opd.val].spcost += UseWt*10^depth(i);
           break;
      case noexp:
           break;
    }
    //指令有左值且指令的類型為復寫指令
    if LIR_Has_Left(inst.kind) && inst.kind != regval
       AdjLsts[inst.left].spcost += DefWt*10^depth(i);
  }
  
  for i = nregs + 1
  {
    //r表示重新計算該值的開銷
    r = Rematerialize(i,nblocks,ninsts,LBlock)
    if r < AdjLsts[i].spcost
       AdjLsts[i].spcost = r;
  }
}

7. 修剪沖突圖

度

假設沒有這個度小于R的節(jié)點時該沖突圖是R著色的，因為這個節(jié)點的度小于R，故至少有一種顏色沒有被與它相鄰的顏色使用，因此這個顏色可以分配給這個度小于R的節(jié)點。

因此我們的做法就是：重復的尋找圖中那些相鄰的節(jié)點數小于R的節(jié)點，每當找到一個這樣的節(jié)點，便將它從圖中刪除，并放到棧中，以便按照逆序對節(jié)著色。

在這個處理過程中每一個刪除節(jié)點會記錄到與之相鄰節(jié)點的rmvadj域值。

如果最后能夠刪除此圖中的所有節(jié)點，就能夠確定該圖是可以R著色的。然后從棧中彈出這些節(jié)點，并給每一個節(jié)點賦予一個顏色。

但是圖中可能會存在度大于R的節(jié)點，在這種情況下，我們應該保持一種樂觀的啟發(fā)式，即選擇一個度大于R且具有最小溢出代價的節(jié)點，并樂觀的將該節(jié)點壓入棧中，我們這樣做的是期望將來它的鄰接點不會用完所有的顏色，因此將應在修剪沖突圖時做出的決定推遲到實際給節(jié)點指派顏色時。

//Prune_Graph函數
do
{
  //根據度

8.著色

//Assign_Regs函數
do
{
  r = stack.pop();
  //返回沒有給r的沖突節(jié)點著色的最小顏色
  c = Min_Color(r);
  if c > 0
  {
    if r <= nregs
    {
      Real_Reg(c) = r;
    }
  }
  else
  {
    //如果無節(jié)點可用，標記該節(jié)點溢出
    AdjLsts[r].spill = true;
    success = false;
  }
}while Stack == []

如果上面的寄存器分配成功則直接修改指令，將符號寄存器修改為真實寄存器。否則要產生溢出符號寄存器相關的指令。

9. 溢出符號寄存器

如果寄存器分配不成功，需要將寄存器溢出到內存中，然后進行寄存器分配。具體的代碼如下：

//Gen_Spill_Code
for i = 1 to nblocks
{
  for j = 1 to ninsts[i]
  {
    inst = LBlock[i][j];
    switch( LIR_Exp_Kind(inst.kind) )
    {
      case binexp:
        //如果二元表達式的opreand1需要spill
        if AdjLsts[inst.opd1.val].spill
        {
          //獲取inst.opd1.val溢出到內存地址
          Comp_Disp(inst.opd1.val);
          //在當前使用opd1的指令之前插入load inst.opd1.val的指令
          insert_before(i,j,ninsts,LBlock,